人教版七年级下册6.1 平方根练习题ppt课件

这是一份人教版七年级下册6.1 平方根练习题ppt课件，文件包含613平方根pptx、613平方根练习题含答案doc、613平方根教案doc等3份课件配套教学资源，其中PPT共9页， 欢迎下载使用。

1．了解平方根的概念，并理解平方与开平方的互逆关系．2．会求非负数的平方根．
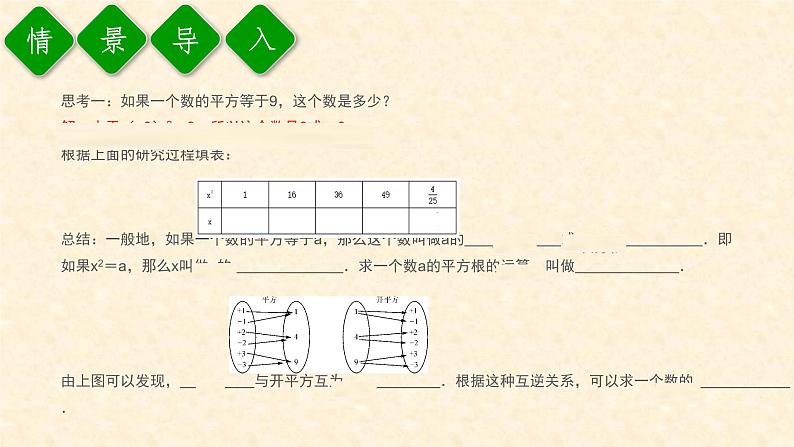
思考一：如果一个数的平方等于9，这个数是多少？解：由于（±3）2＝9，所以这个数是3或－3.根据上面的研究过程填表：总结：一般地，如果一个数的平方等于a，那么这个数叫做a的 或 ．即如果x2＝a，那么x叫做a的 ．求一个数a的平方根的运算，叫做 ．由上图可以发现， 与开平方互为 ．根据这种互逆关系，可以求一个数的 ．
思考二：正数的平方根有什么特点？0的平方根是多少？负数有平方根吗？我们发现，正数的平方根有 个，它们互为 ，其中正的平方根就是这个数的 ．因为02＝0，并且任何一个不为0的数的平方都不等于0，所以0的平方根是 ．正数的平方是正数，0的平方是0，负数的平方也是 ，即在我们所认识的数中，任何一个数的平方都不会是 ，所以负数没有 ．归纳：正数有 个平方根，它们互为 ；0的平方根是 ；负数 平方根．我们知道，正数a的算术平方根可以用 表示；正数a的负的平方根，可以用符号“ ”表示，故正数a的平方根可以用符号“ ”表示，读作“ ”．注意：符号 只有当a 0时有意义，当a 0时无意义．
例1　（教材P45例4）求下列各数的平方根：（1）100；　（2） ；　（3）0.25.【解答】　（1）因为（±10）2＝100，所以100的平方根是±10.（2）因为 ，所以 的平方根是 .（3）因为（±0.5）2＝0.25，所以0.25的平方根是±0.5.例2　（教材P46例5）求下列各式的值：（1） ；　（2） ；　（3） .【解答】（1）因为62＝36，所以 ＝6.（2）因为0.92＝0.81，所以 ＝－0.9.（3）因为 ，所以 .思考：知道一个数的算术平方根，就可以立即写出它的负的平方根，为什么？因为这个数的负的平方根是它的算术平方根的相反数．
【跟踪训练1】　9的平方根是（ A ）A．±3 B． C．3 D．－3【跟踪训练2】　16的平方根是 ， 的平方根是 ．【跟踪训练3】　求下列各数的平方根：（1）121；　（2）0.81；　（3） ；　（4）0.解：（1） ＝±11.（2） ＝±0.9.（3） ；（4） ＝0.
1．下列说法错误的是（ D ）A. ＝0.4 B． ＝±0.5 C．3是9的一个平方根 D．0没有平方根2．a是 的平方根，b是 的算术平方根，则a＋b＝（ B ）A． B. C. D．3．已知一个正数x的两个平方根是a＋1和a－3，则a的值是 ．4．求下列各式的值：（1） ；（2） ；（3） ；（4） .解：（1）±1.7.（2） .（3） .（4）±11.
1．一般地，如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根．即如果x2＝a，那么x叫做a的平方根．求一个数a的平方根的运算，叫做开平方．平方与开平方互为逆运算．2．正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．3．平方根与算术平方根的联系与区别：联系：（1）包含关系：平方根包含算术平方根，算术平方根是平方根的一种；（2）只有非负数才有平方根和算术平方根；（3）0的平方根是0，算术平方根也是0.区别：（1）个数不同：一个正数有两个平方根，但只有一个算术平方根；（2）表示法不同：平方根表示为 ，而算术平方根表示为 .