初中1.3 截一个几何体同步达标检测题

专题1.3截一个几何体

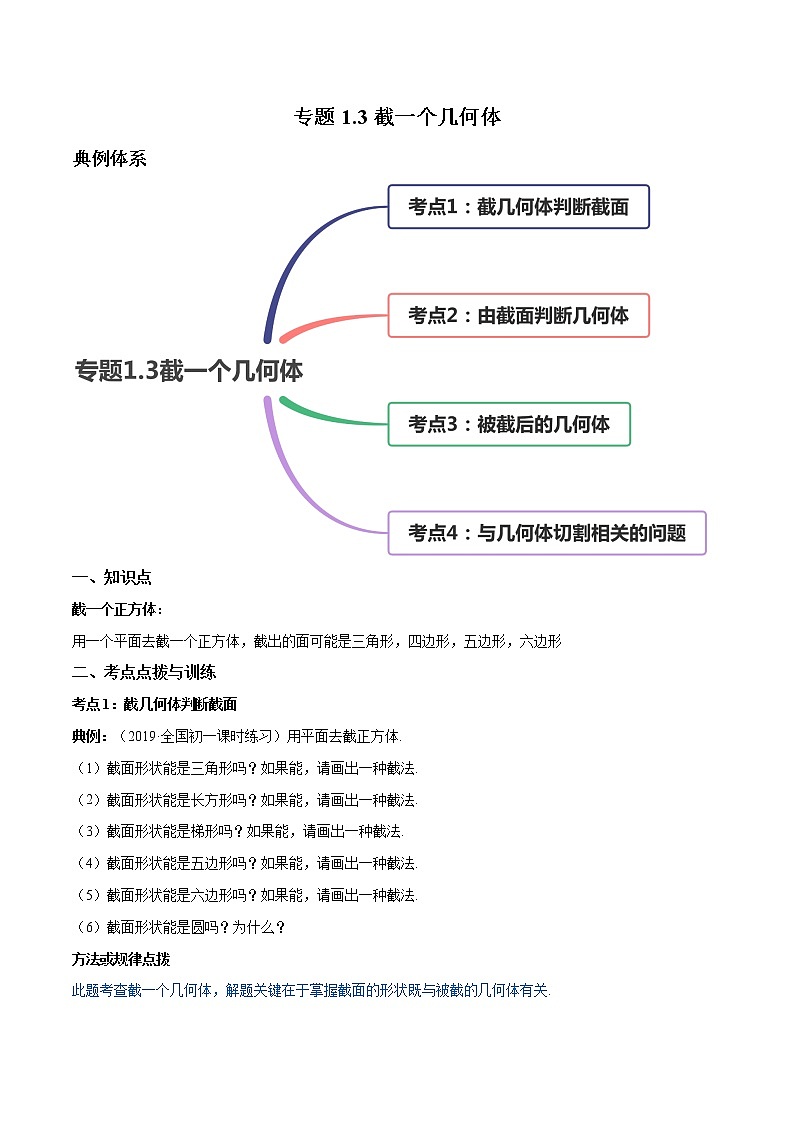
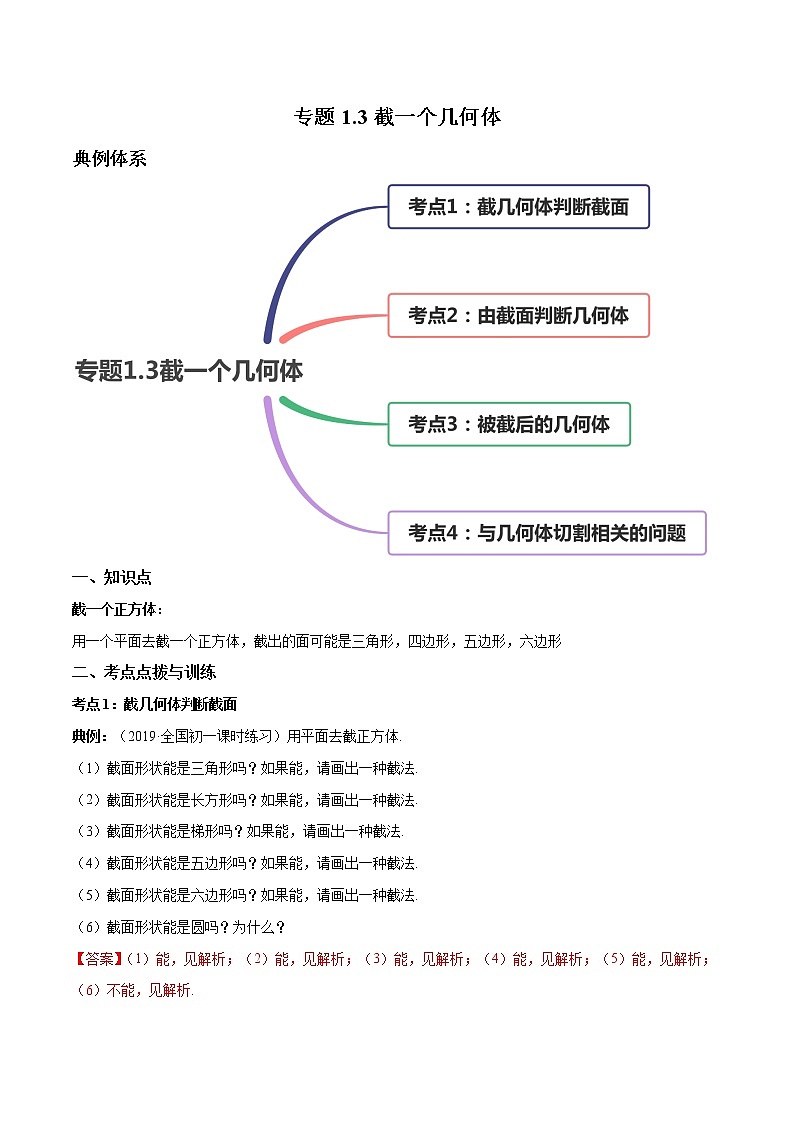
典例体系

一、知识点

截一个正方体：

用一个平面去截一个正方体，截出的面可能是三角形，四边形，五边形，六边形

二、考点点拨与训练

考点1：截几何体判断截面

典例：（2019·全国初一课时练习）用平面去截正方体.

（1）截面形状能是三角形吗？如果能，请画出一种截法.

（2）截面形状能是长方形吗？如果能，请画出一种截法.

（3）截面形状能是梯形吗？如果能，请画出一种截法.

（4）截面形状能是五边形吗？如果能，请画出一种截法.

（5）截面形状能是六边形吗？如果能，请画出一种截法.

（6）截面形状能是圆吗？为什么？

方法或规律点拨

此题考查截一个几何体，解题关键在于掌握截面的形状既与被截的几何体有关.

巩固练习

1．（2020·重庆八中初三期末）用一个平面去截一个圆锥，截面的形状不可能是(   )

A．圆 B．矩形 C．椭圆 D．三角形

2．（2019·山东省初一期中）用一个平面去截一个正方体，截面可能是（      ）

A．七边形 B．圆 C．长方形 D．圆锥

3．（2019·山西省初一期中）用一个平面去截一个立体图形，当截取的角度和方向不同时，截面的形状随截法的不同而改变，下列截面中属于三角形的是（  ）

A． B． C． D．

4．（2020·湖北省黄石八中初三一模）圆锥的轴截面是(      )

A．梯形 B．等腰三角形 C．矩形 D．圆

5．（2019·临泽县教育体育和科学技术局初一月考）一个几何体的一个截面是三角形，则原几何体一定不是下列图形中的(      )

A．圆柱和圆锥 B．球体和圆锥 C．球体和圆柱 D．正方体和圆锥

6．（2019·沈阳市第一二六中学初一月考）用一个平面按照如图所示的位置与正方体相截，则截面图形是（   ）

A． B． C． D．

7．（2019·菏泽市牡丹区第二十一初级中学初一月考）用一个平面去截一个几何体，如果截面的形状是长方形，那么这个几何体不可能是（    ）．

A．圆柱 B．圆锥 C．五棱柱 D．正方体

8．（2019·重庆一中初一月考）用一个平面去截一个正方体，截面不可能是（       ）

A．梯形 B．五边形 C．六边形 D．七边形

9．（2019·青岛大学附属中学初一月考）用一个平面去截①圆锥、②圆柱、③球、④五棱柱，能得到的截面是圆的图形是（    ）

A．②④ B．①②③ C．②③④ D．①③④

10．（2019·全国初一课时练习）一个圆柱的底面半径是10 cm，高是18 cm，把这个圆柱放在水平桌面上，如图所示．

(1)如果用一个平面沿水平方向去截这个圆柱，所得的截面是什么形状？

(2)如果用一个平面沿竖直方向去截这个圆柱，所得的截面是什么形状？

(3)怎样截时所得的截面是长方形且长方形的面积最大，请你画出这个截面并求其面积．

考点2：由截面判断几何体

典例：（2018·全国初一单元测试）用平面截几何体可得到平面图形，在表示几何体的字母后填上它可截出的平面图形的号码．

如：A(1，5，6)，则B(________)；C(________)；D(________)．

方法或规律点拨

熟悉“常见几何体的常见截面图形”是解答本题的关键.

巩固练习

1．（2018·四川省双流县棠湖中学实验学校初一月考）下面几何体的截面图可能是圆的是（　　）

A．圆锥    B．正方体    C．长方体    D．棱柱

2．（2019·闽清县教育局初一期末）用一个平面去截下列3个几何体，能得到截面是长方形的几何体有（　　）

A．0个 B．1个 C．2个 D．3个

3．（2019·西安交大阳光中学初一月考）用一个平面去截一个几何体，截面形状为三角形，则这个几何体可能为：

①正方体；②圆柱；③圆锥；④正三棱柱. （   ）

A．①②③④ B．①③④ C．①④ D．①②

4．（2020·山东省初一期中）用一个平面取截一个几何体，得到的截面是四边形，这个几何体可能是（   ）

A．圆柱 B．球体 C．圆锥 D．以上都有可能

5．（2020·宁夏回族自治区景博中学初一期末）如图，用一个平面去截下列立体图形，截面可以得到三角形的立体图形有（        ）

A．4个 B．3个 C．2个 D．1个

6．（2020·甘肃省初一期末）用一个平面去截一个几何体，如果截面的形状是圆，则这个几何体不可能是（　　）

A．圆柱; B．圆锥; C．正方体; D．球

7．（2019·四川省成都市七中育才学校初一月考）(1)用一个平面去截一个几何体，可以得到圆形的截面的几何体有？

(2)用一个平面去截一个几何体，可以得到三角形的截面的几何体有？

8．（2019·全国初一课时练习）一物体的外形为正方体，为探明其内部结构，用一组沿竖直方向（自左向右）的平面截这个物体，得到如图所示的一组截面，请你猜猜这个正方体的内部构造.

考点3：被截后的几何体

典例：（2019·山东省初一期中）一个正方体锯掉一个角后，顶点的个数是（    ）

A．7个 B．8个 C．9个 D．7个或8个或9个或10个

方法或规律点拨

本题结合截面考查正方体的相关知识，对于一个正方体：截去一个角，则其顶点的个数有三种情况：减少1；不变；增加1或2．

巩固练习

1．（2019·广东省初一月考）用一个平面去截一个正方体,下列选项中画有阴影的部分是截面,哪个画法是错误的(　　)

A． B． C． D．

2．（2019·山东省初一期中）如图，一正方体截去一角后，剩下的几何体的面数和棱数分别为（    ）

A．6，14 B．7，15 C．7，14 D．6，15

3．（2018·河南省初一期末）将一个长方体截去一个角得到一个如图所示的新几何体，这个新几何体有_____个面．

4．（2019·浙江省初三二模）把一个长方体切去一个角后，剩下的几何体的顶点个数为__．

5．（2019·山西省初一期末）钻石原石看起来并不起眼，但经过精心设计、切割、打磨，就会成为璀璨夺目的钻石．钻石切割是多面体截面在实际生活中的一个应用．将已经加工成三棱柱形状的钻石原石进行切割，只切一刀，切截面的形状可能是___________．（填一种情况即可）

6．（2019·山东省初一期中）如果用平面截掉一个长方体的一个角（即切去一个三棱锥），则剩下的几何体最多有_____顶点，最少有_____条棱．

7．（2018·江苏省初一月考）如图①是圆柱被一个平面斜切后得到的几何体，类比梯形面积公式的推导方法(如图②) ，推导图①中的几何体的体积为_________.

8．（2019·全国初一专题练习）如图，图（1）是正方体木块，把它切去一块，可能得到（2）、（3）、（4）、（5）所示的图形，问（2）、（3）、（4）、（5）图中切掉的部分可能是其他几块中的哪一块?

9．（2020·贵州省初一期末）如图，将正方体沿面AB′C剪下，则截下的几何体为（   ）

A．三棱锥

B．三棱柱

C．四棱锥

D．四棱柱

考点4：与几何体切割相关的问题

典例：（2019·河南省初一期中）一块长方体豆腐切三刀，最多能切成的块数（形状，大小不限）是（　　）

A．10 B．8 C．7 D．6

方法或规律点拨

本题考查了切长方体的问题，掌握切长方体的性质是解题的关键．

巩固练习

1．（2020·河南省初一期末）如图，一个有盖的圆柱形玻璃杯中装有半杯水，若任意放置这个水杯，则水面的形状不可能是

A． B． C． D．

2．（2020·银川外国语实验学校初一期末）如图，在一密闭的圆柱形玻璃杯中装一半的水，水平放置时，水面的形状是（　　）

A．圆 B．长方形 C．椭圆 D．平行四边形

3．（2018·全国初一单元测试）爸爸给儿子阳阳买了一个生日蛋糕(圆柱形)，阳阳想把蛋糕切成至少七块分给七位小朋友，若沿竖直方向切分，则至少需切________刀．

4．（2018·修水县大椿乡中学初一期中）小明的妈妈烙了一张大饼，需要切开吃，小方没有碰触大饼，而是直接用刀切了三次，她最多能把这张饼切成___________块.

5．（2018·全国初一课时练习）一块方形蛋糕，一刀切成相等的两块，两刀最多切成4块，试问：五刀最多可切成__ 块相等体积的蛋糕，十刀最多可切成____块（要求：竖切，不移动蛋糕）．

6．（2019·河南省初一期中）如图所示是一个圆柱体，它的底面半径为3cm，高为6cm．

（1）请求出该圆柱体的表面积；

（2）用一个平面去截该圆柱体，你能截出截面最大的长方形吗？截得的长方形面积的最大值为多少？

7．（2019·四川省西航港一中初一月考）如图所示，长方形ABCD的长AB为10  cm，宽AD为6 cm，把长方形ABCD绕AB边所在的直线旋转一周，然后用平面沿AB方向去截所得的几何体，求截面的最大面积．

8．（2019·全国初一课时练习）如图①是一个正方体，不考虑边长的大小，它的平面展开图为图②，四边形APQC是截正方体的一个截面．问截面的四条线段AC，CQ，QP，PA分别在展开图的什么位置上？