2021-2022学年八年级数学下册第20章数据的整理与初步处理20.3数据的离散程度第2课时学案 华东师大版
展开20.3.2 数据分析的应用
【学习目标】
1.进一步加深理解平均数、方差、标准差的概念;
2.会结合实际,运用相应的知识解决问题,体会样本估计总体的思想。
【学习准备】
课前,从事下列活动:
(1)两人一组,在安静的环境中,一人估计1min的时间,另一人记下实际时间,将结果记录下来。
(2)在吵闹的环境中,再做一次这样的实验。
【学习过程】
活动1:根据图表感受数据的稳定性
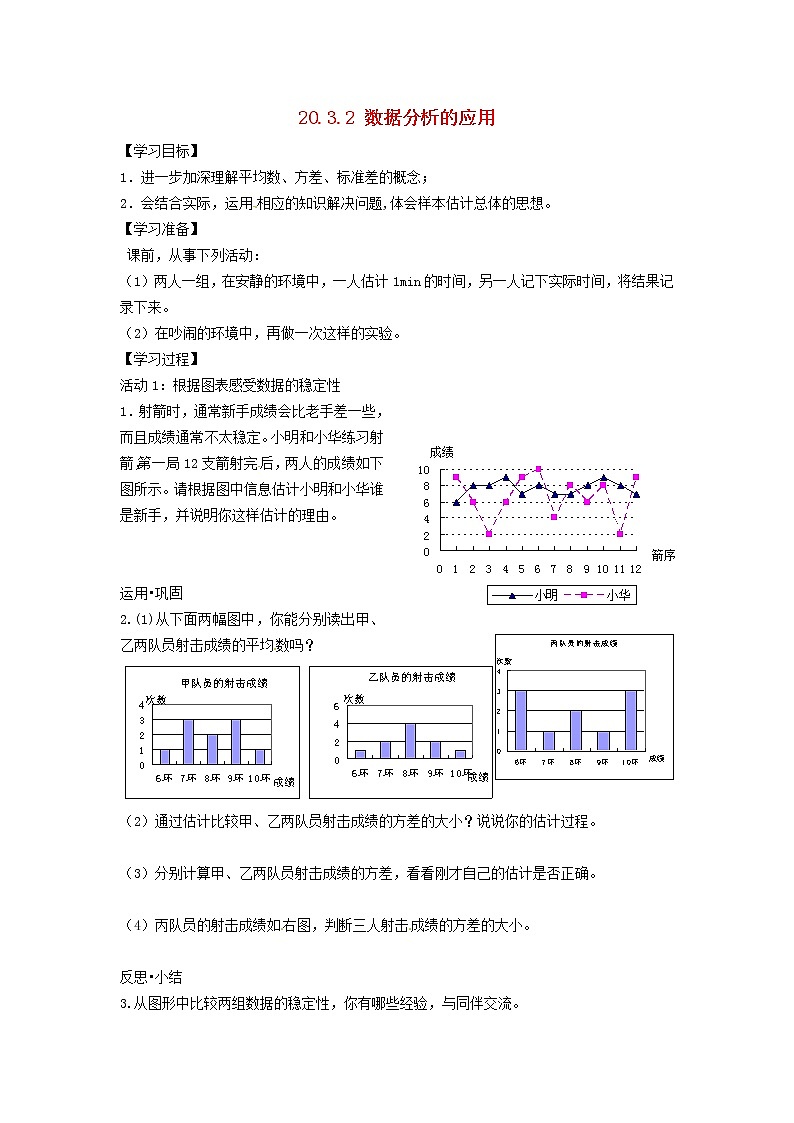
1.射箭时,通常新手成绩会比老手差一些,而且成绩通常不太稳定。小明和小华练习射箭,第一局12支箭射完后,两人的成绩如下图所示。请根据图中信息估计小明和小华谁是新手,并说明你这样估计的理由。
运用•巩固
2.(1)从下面两幅图中,你能分别读出甲、乙两队员射击成绩的平均数吗?
(2)通过估计比较甲、乙两队员射击成绩的方差的大小?说说你的估计过程。
(3)分别计算甲、乙两队员射击成绩的方差,看看刚才自己的估计是否正确。
(4)丙队员的射击成绩如右图,判断三人射击成绩的方差的大小。
反思•小结
3.从图形中比较两组数据的稳定性,你有哪些经验,与同伴交流。
活动2:感受生活中的稳定性
1.将全班课前收集的数据汇总起来,分别计算安静状态和吵闹环境下估计结果的平均值和方差。
2.两种情况下的结果是否一致,说说你的理由。
活动3:利用数据的稳定性做出抉择
1.某校拟派一名跳高运动员参加一项校际比赛,对甲、乙两名跳高运动员进行了8次选拔比赛,他们的成绩(单位:米)分别如下:
甲:1.70,1.65,1.68,1.69,1.72,1.73,1.68,1.67。
乙:1.60,1.73,1.72,1.61,1.62,1.71,1.70,1.75。
(1)甲、乙两名运动员的跳高的平均成绩分别是多少?
(2)他们哪个的成绩更为稳定?
(3)经预测,跳高1.65米就很可能获得冠军,该校为了获取跳高比赛冠军,可能选哪位运动员参赛?若预测1.70方可夺得冠军呢?
活动4:自主反馈
1.为选派一名学生参加全市实践活动技能竞赛,A、B两位同学在校实习基地现场进行加工直径为20mm的零件测试,他俩各加工的10个零件的相关数据依次如下图表所示(单位:mm)。
| 平均数 | 方差 | 完全符合要求个数 |
A | 20 | 0.026 | 2 |
B | 20 | S2B | 5 |
根据测试得到的有关数据,试解答下列问题:
(1)考虑平均数与完全符合要求的个数,你认为__________的成绩好些。
(2)计算出S2B的大小,考虑平均数与方差,说明谁的成绩好些。
*2.姚明在2005-2006赛季NBA常规赛中表现优异。下面是他在这个赛季中,分别与“超音速”和“快船”队各四场比赛中的技术统计。
场次 | 对阵超音速 | 对阵快船 | ||||
得分 | 篮板 | 失误 | 得分 | 篮板 | 失误 | |
第一场 | 22 | 10 | 2 | 25 | 17 | 2 |
第二场 | 29 | 10 | 2 | 29 | 15 | 0 |
第三场 | 24 | 14 | 2 | 17 | 12 | 4 |
第四场 | 26 | 10 | 5 | 22 | 7 | 2 |
(1)请分别计算姚明在对阵“超音速”和“快船”两队各四场比赛中,平均每场得分是多少?
(2)请你从得分的角度分析,姚明在与“超音速”和“快船”的比赛中,对阵哪一个队的发挥比较稳定?
(3)如果规定“综合得分”为:平均每场得分×1 + 平均每场篮板×1.2+平均每场失误×(-1),且综合得分越高表现越好,那么请你利用这种评价方法,来比较姚明在与“超音速”和“快船”的比赛中,对阵哪一个队表现更好?









