专题4.4小题易丢分期末考前必做选择30题（提升版）-2021-2022学年七年级数学下学期期末考试高分直通车【北师大版】

这是一份专题4.4小题易丢分期末考前必做选择30题（提升版）-2021-2022学年七年级数学下学期期末考试高分直通车【北师大版】，文件包含专题44小题易丢分期末考前必做选择30题提升版-2021-2022学年七年级数学下学期期末考试高分直通车解析版北师大版docx、专题44小题易丢分期末考前必做选择30题提升版-2021-2022学年七年级数学下学期期末考试高分直通车原卷版北师大版docx等2份试卷配套教学资源，其中试卷共24页， 欢迎下载使用。

注意事项：
本试卷共30题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级、座号填写在试卷规定的位置．
一．选择题（共30小题）
1．（2021•无棣县一模）四个运算：①a3+a2＝a5；②12a-1=12a；③a6÷a3＝a2；④（a﹣1）（a+2）＝a2﹣2．运算结果正确的是（ ）
A．①B．②C．③D．④
【分析】由相关整式运算法则逐一判断即可．
【解析】a3+a2不是同类项，不能合并，①不正确，故A不符合题意；
12a﹣1=12a，②正确，故B符合题意；
a6÷a3＝a3，③不正确，故C不符合题意；
（a﹣1）（a+2）＝a2+a﹣2，④不正确，故D不符合题意，
故选：B．
2．（2020秋•海珠区期末）已知a+b＝6，ab＝﹣2，则a2+b2的值是（ ）
A．36B．40C．42D．32
【分析】根据完全平方公式：（a+b）2＝a2+2ab+b2进行计算即可．
【解析】∵（a+b）2＝a2+2ab+b2，a+b＝6，ab＝﹣2，
∴a2+b2＝（a+b）2﹣2ab＝36﹣2×（﹣2）＝40，
故选：B．
3．（2020秋•平邑县期末）如果x2+kx+14是完全平方式，则k的值是（ ）
A．12B．±1C．±12D．1
【分析】利用完全平方公式的结构特征判断即可确定出k的值．
【解析】∵x2+kx+14是完全平方式，
∴k=±2×1×12=±1，
故选：B．
4．（2020春•镇海区期末）如图有两张正方形纸片A和B，图1将B放置在A内部，测得阴影部分面积为2，图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为20，若将3个正方形A和2个正方形B并列放置后构造新正方形如图3，（图2，图3中正方形AB纸片均无重叠部分）则图3阴影部分面积（ ）
A．22B．24C．42D．44
【分析】由图1可知，阴影部分面积a2﹣b2＝2，图2可知，阴影部分面积（a+b）2﹣a2﹣b2＝20，进而得到ab＝10，由图3可知，阴影部分面（2a+b）2﹣3a2﹣2b2＝a2﹣b2+4ab＝2+40＝42．
【解析】由图1可知，阴影部分面积a2﹣b2＝2，
图2可知，阴影部分面积（a+b）2﹣a2﹣b2＝20，
所以ab＝10，
由图3可知，阴影部分面（2a+b）2﹣3a2﹣2b2＝a2﹣b2+4ab＝2+40＝42．
故选：C．
5．（2020秋•宜宾期末）若a+b＝﹣3，ab＝﹣10，则a﹣b的值是（ ）
A．0或7B．0或﹣13C．﹣7或7D．﹣13或13
【分析】先由（a+b）2﹣4ab＝（a﹣b）2，再根据已知条件可得（a﹣b）2的值，即可得出答案．
【解析】∵（a﹣b）2＝（a+b）2﹣4ab，
∴（a﹣b）2＝（﹣3）2﹣4×（﹣10）＝49，
∴a﹣b＝±7．
故选：C．
6．（2020秋•鹿邑县期末）已知8x＝10，2y＝4，则23x+2y的值为（ ）
A．40B．80C．160D．240
【分析】所求式子根据积的乘方与幂的乘方的逆运算进行化简，再整体代入计算即可．
【解析】∵8x＝10，2y＝4，
∴原式＝（23）x•（2y）2＝8x•（2y）2＝10×42＝160．
故选：C．
7．（2020秋•平阴县期末）如图，直线l1∥l2，∠1＝50°，∠2＝75°，则∠3＝（ ）
A．55°B．60°C．65°D．70°
【分析】根据平行线的性质，可以得到∠1＝∠4，再根据对顶角相等和三角形内角和，即可求得∠3的度数
【解析】∵直线l1∥l2，
∴∠1＝∠4，
∵∠1＝50°，∠2＝75°，∠2＝∠5，
∴∠4＝50°，∠5＝75°，
∵∠4+∠5+∠3＝180°，
∴∠3＝180°﹣∠4﹣∠5＝180°﹣50°﹣75°＝55°，
故选：A．
8．（2020秋•随县期末）如图，直线AB，CD交于点O，射线OM平分∠AOC，如果∠AOD＝104°，那么∠MOC等于（ ）
A．38°B．37°C．36°D．52°
【分析】根据邻补角互补求出∠AOC的度数，再根据角平分线的定义即可得解．
【解析】∵∠AOD＝104°，
∴∠AOC＝180°﹣∠AOD＝76°，
∵射线OM平分∠AOC，
∴∠MOC=12∠AOC=12×76°＝38°，
故选：A．
9．（2020秋•瑶海区期末）如图，∠AOB＝90°，在下面的四个式子中：①180°﹣∠2；②∠3；③2∠1+∠2；④2∠3﹣2∠1﹣∠2，可以表示为∠2的补角的式子的个数是（ ）
A．1B．2C．3D．4
【分析】根据互补的两角之和为180°，进行判断即可．
【解析】①∵180°﹣∠2+∠2＝180°，
∴180°﹣∠2可以表示∠2的补角，
故①可以表示∠2的补角；
②∵∠3+∠2＝180°，
∴∠3可以表示∠2的补角，
故②可以表示∠2的补角；
③∵∠1+∠2＝∠AOB＝90°，
∴2∠1+∠2＝2（90°﹣∠2）+∠2＝180°﹣∠2，
∵180°﹣∠2+∠2＝180°，
∴2∠1+∠2可以表示∠2的补角，
故③可以表示∠2的补角；
④2∠3﹣2∠1﹣∠2＝2（180°﹣∠2）﹣2（90°﹣∠2）﹣∠2＝360°﹣2∠2﹣180°+2∠2﹣∠2＝180°﹣∠2，
∵180°﹣∠2+∠2＝180°，
∴2∠3﹣2∠1﹣∠2可以表示∠2的补角，
故④可以表示∠2的补角；
故选：D．
10．（2020秋•香坊区期末）如图，下列条件：①∠1＝∠5；②∠2＝∠6；⑧∠3＝∠7；④∠4＝∠8．其中能判定AB∥CD的是（ ）
A．①②B．②③C．①④D．②④
【分析】根据平行线的判定方法对四个条件分别进行判断即可．
【解析】①∵∠1＝∠5，
∴AB∥CD，能判定AB∥CD；
②∵∠2＝∠6，
∴AD∥BC，不能判定AB∥CD；
③∵∠3＝∠7；
∴AD∥BC，不能判定AB∥CD；
④∵∠4＝∠8，
∴AB∥CD，能判定AB∥CD．
故选：C．
11．（2020秋•赫山区期末）2020年益阳始建高铁站，该站建设初期需要运送大量的土石方，某运输公司承担了运送总量为106m3土石方的任务，该运输公司平均运送土石方的速度v（单位：m3/天）与完成运送任务所需的时间t（单位：天）之间的函数关系式是（ ）
A．v=106tB．v＝106C．v=1106t2D．v＝106t2
【分析】按照运送土石方总量＝平均运送土石方的速度vX完成运送任务所需时间t，列出等式，然后变形得出v关于t的函数，观察选项可得答案．
【解析】由题意可得，vt＝106，
∴v=106t．
故选：A．
12．（2020秋•下城区期末）把一个长为5，宽为2的长方形的长减少x（0≤x＜5），宽不变，所得长方形的面积y关于x的函数表达式为（ ）
A．y＝10﹣xB．y＝5xC．y＝2xD．y＝﹣2x+10
【分析】用代数式表示出变化后长方形的长，面积即可．
【解析】变化后长方形的长为（5﹣x），宽为2，因此面积y＝2（5﹣x）＝﹣2x+10，
故选：D．
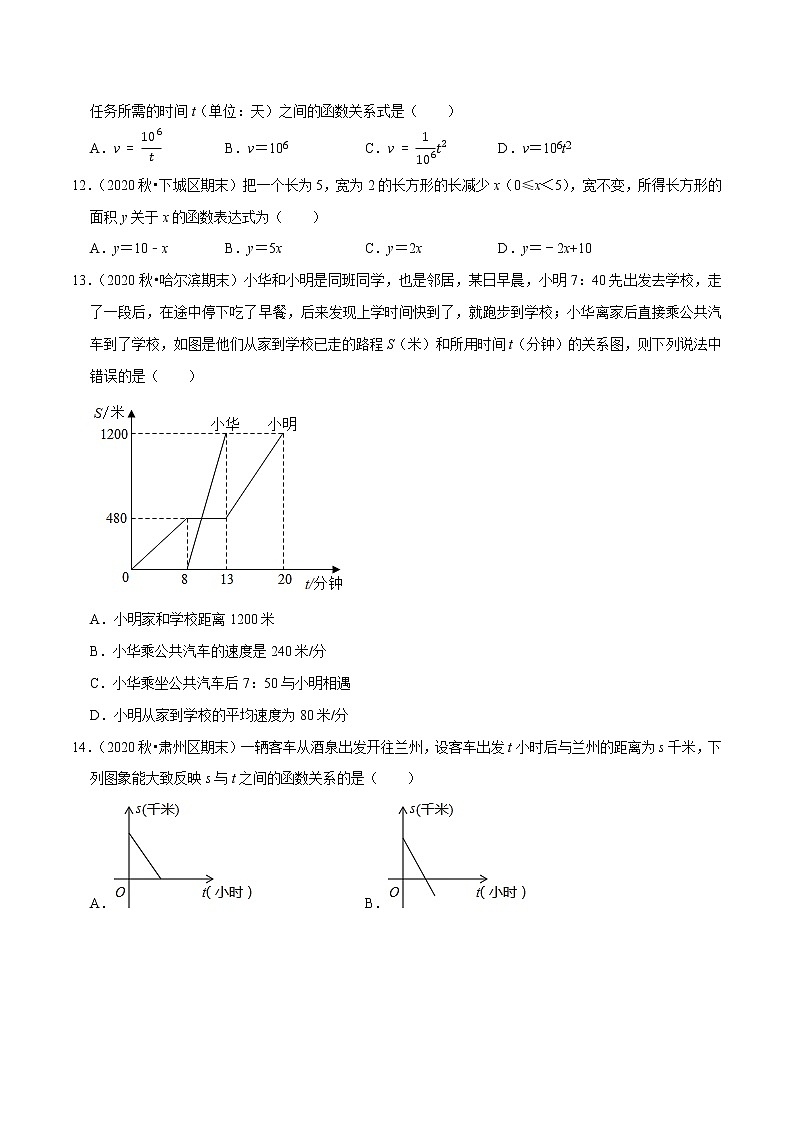
13．（2020秋•哈尔滨期末）小华和小明是同班同学，也是邻居，某日早晨，小明7：40先出发去学校，走了一段后，在途中停下吃了早餐，后来发现上学时间快到了，就跑步到学校；小华离家后直接乘公共汽车到了学校，如图是他们从家到学校已走的路程S（米）和所用时间t（分钟）的关系图，则下列说法中错误的是（ ）
A．小明家和学校距离1200米
B．小华乘公共汽车的速度是240米/分
C．小华乘坐公共汽车后7：50与小明相遇
D．小明从家到学校的平均速度为80米/分
【分析】根据已知信息和函数图象的数据，一次解答每个选项
【解析】由图象可知，小华和小明的家离学校1200米，故A正确；
根据图象，小华乘公共汽车，从出发到到达学校共用了13﹣8＝5（分钟），所以公共汽车的速度为1200÷5＝240（米/分），故B正确；
小明先出发8分钟然后停下来吃早餐，由图象可知在小明吃早餐的过程中，小华出发并与小明相遇然后超过小明，所以二人相遇所用的时间是8+480÷240＝10（分钟），即7：50相遇，故C正确；
小明从家到学校的时间为20分钟，所以小明的平均速度为1200÷20＝60（米/分），故D错误．
故选：D．
14．（2020秋•肃州区期末）一辆客车从酒泉出发开往兰州，设客车出发t小时后与兰州的距离为s千米，下列图象能大致反映s与t之间的函数关系的是（ ）
A．B．
C．D．
【分析】因为匀速行驶，图象为线段，时间和路程是正数，客车从酒泉出发开往兰州，火车与兰州的距离越来越近，路程由大变小，由此选择合理的答案．
【解析】根据出发时与终点这两个特殊点的意义，图象能大致反映s与t之间的函数关系的是应选A．
故选：A．
15．（2020秋•海珠区期末）如图，将△ABC沿直线DE折叠后，使得点B与点A重合，若AC＝5，BC的长为12，则△ADC的周长为（ ）
A．17B．10C．12D．22
【分析】由折叠的性质可得AD＝BD，即可求解．
【解析】∵将△ABC沿直线DE折叠，
∴AD＝BD，
∴△ADC的周长＝AD+AC+CD＝BC+AC＝17，
故选：A．
16．（2020秋•海珠区期末）如图，Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于点D，AB＝18，S△ABD＝27，则CD的长为（ ）
A．4B．8C．3D．6
【分析】过点D作DE⊥AB于E，根据角平分线上的点到角的两边距离相等可得DE＝CD，然后利用△ABD的面积公式列式计算即可得解．
【解析】如图，过点D作DE⊥AB于E，
∵∠C＝90°，AD平分∠BAC，
∴DE＝CD，
∴S△ABD=12AB•DE=12×18•DE＝27，
解得：DE＝3，
∴CD＝3．
故选：C．
17．（2020秋•海珠区期末）下列四种网络运营商的标志中，轴对称图形的是（ ）
A．B．
C．D．
【分析】利用轴对称图形的定义进行解答即可．
【解析】A、不是轴对称图形，故此选项不合题意；
B、不是轴对称图形，故此选项不合题意；
C、不是轴对称图形，故此选项不合题意；
D、是轴对称图形，故此选项符合题意；
故选：D．
18．（2020秋•平邑县期末）等腰三角形的一个内角为50°，它的顶角的度数是（ ）
A．65°B．80°C．65°或80°D．50°或80°
【分析】可知有两种情况（顶角是50°和底角是50°时），由等边对等角求出底角的度数，用三角形的内角和定理即可求出顶角的度数．
【解析】如图所示，△ABC中，AB＝AC．
有两种情况：
①顶角∠A＝50°；
②当底角是50°时，
∵AB＝AC，
∴∠B＝∠C＝50°，
∵∠A+∠B+∠C＝180°，
∴∠A＝180°﹣50°﹣50°＝80°，
∴这个等腰三角形的顶角为50°或80°．
故选：D．
19．（2020秋•沙坪坝区期末）如图，△ABC中，AB＝AC，∠BAC＝100°，AD是BC边上的中线，CE平分∠BCA交AB于点E，AD、CE相交于点F，则∠CFA的度数是（ ）
A．100°B．105°C．110°D．120°
【分析】根据等腰三角形的性质可求∠ACB，根据角平分线的性质可求∠BCE，根据三角形三线合一的性质可求∠ADC，再根据三角形外角的性质可求∠CFA．
【解析】在△ABC中，AB＝AC，∠BAC＝100°，
∴∠ACB＝（180°﹣100°）÷2＝40°，
∵CE平分∠BCA，
∴∠BCE＝20°，
∵AD是BC边上的中线，
∴∠ADC＝90°，
∴∠CFA＝90°+20°＝110°．
故选：C．
20．（2020秋•南浔区期末）如图，已知△ABC中，AB＝AC，点D，E是射线AB上的两个动点（点D在点E的右侧），且CE＝DE，连接CD，若∠ACE＝x°，∠BCD＝y°，则y关于x的函数关系式是（ ）
A．y＝90﹣x（0＜x＜180°）B．y=12x（0＜x＜180°）
C．y＝90-23x（0＜x＜180°）D．y=23x（0＜x＜180°）
【分析】根据等腰三角形的性质得出∠ACB＝∠ABC＝x°+∠BCE和∠ADC＝∠DCE＝y°+∠BCE，由三角形外角的性质得出∠ABC＝∠ADC+∠BCD，即x°+∠BCE＝y°+∠BCE+y°，即x＝2y，可得y关于x的函数关系式．
【解析】在△ABC中，AB＝AC，
∴∠ACB＝∠ABC＝x°+∠BCE，
∵CE＝DE，
∴∠ADC＝∠DCE＝y°+∠BCE，
∵∠ABC＝∠ADC+∠BCD，即x°+∠BCE＝y°+∠BCE+y°，即x＝2y，
∴y关于x的函数关系式为y=12x（0＜x＜180°）．
故选：B．
21．（2020秋•巩义市期末）下列事件中，属于随机事件的是（ ）
A．掷一枚硬币10次，仅有1次正面朝上
B．三角形的三个内角之和等于180°
C．从装有5个红球的袋子里摸出一个白球
D．在地面向上抛出一个篮球还会下落
【分析】根据事件发生的可能性大小判断相应事件的类型即可．
【解析】A、掷一枚硬币10次，仅有1次正面朝上是随机事件；
B、三角形的三个内角之和等于180°是必然事件；
C、从装有5个红球的袋子里摸出一个白球是不可能事件；
D、在地面向上抛出一个篮球还会下落是必然事件．
故选：A．
22．（2020秋•南平期末）在一个不透明的袋子中装有5个小球，小球除颜色外完全相同，其中黑球2个，红球3个，从中随机摸出一个小球，则摸出的小球是红色的概率是（ ）
A．32B．23C．25D．35
【分析】用红色小球的个数除以球的总个数即可．
【解析】∵从中随机摸出一个小球，共有5种等可能结果，其中摸出的小球是红色的有3种结果，
∴摸出的小球是红色的概率为35，
故选：D．
23．（2020秋•九龙坡区期末）下列说法：①不可能事件发生的概率为0；②随机事件发生的概率为12；③事件发生的概率与实验次数无关；④“画一个矩形，其对角线互相垂直”是必然事件．其中正确的是（ ）
A．①②B．②③C．①③D．①④
【分析】根据事件的概念：事件分为确定事件和不确定事件（随机事件），确定事件又分为必然事件和不可能事件，其中，①必然事件发生的概率为1，即P（必然事件）＝1；②不可能事件发生的概率为0，即P（不可能事件）＝0；③如果A为不确定事件（随机事件），那么0＜P（A）＜1，逐一判断即可得到答案．
【解析】①不可能事件发生的概率为0，说法正确；
②随机事件发生的概率为0到1，故说法错误；
③事件发生的概率与实验次数无关，故说法正确；
④“画一个矩形，其对角线互相垂直”是随机事件，故说法错误．
正确的说法有：①③．
故选：C．
24．（2020秋•海珠区期末）下列各组图形中，表示AD是△ABC中BC边的高的图形为（ ）
A．B．
C．D．
【分析】根据高的定义：”过三角形的顶点向对边作垂线，顶点和垂足之间的线段叫做三角形的高线“解答．
【解析】△ABC的高AD是过顶点A与BC垂直的线段，只有D选项符合．
故选：D．
25．（2020秋•播州区期末）在正方形方格纸中，每个小方格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形，如图是5×7的正方形方格纸，以点D，E为两个顶点作格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（ ）
A．2个B．4个C．6个D．8个
【分析】根据图形可知BC＝DE，再根据全等三角形的判定定理得出答案即可．
【解析】
与△ABC全等的三角形有△DEF，△DEQ，△DER，△DEW，共4个三角形，
故选：B．
26．（2020秋•福州期末）如图，点F，C在BE上，AC＝DF，BF＝EC，AB＝DE，AC与DF相交于点G，则与2∠DFE相等的是（ ）
A．∠A+∠DB．3∠BC．180°﹣∠FGCD．∠ACE+∠B
【分析】根据等式的性质得出BC＝EF，进而利用SSS证明△ABC与△DEF全等，利用全等三角形的性质得出∠ACB＝∠DFE，最后利用三角形内角和解答．
【解析】∵BF＝EC，
∴BF+FC＝EC+FC，
∴BC＝EF，
在△ABC与△DEF中，
AC=DFAB=DEBC=EF，
∴△ABC≌△DEF（SSS），
∴∠ACB＝∠DFE，
∴2∠DFE＝180°﹣∠FGC，
故选：C．
27．（2020秋•大安市期末）如图，BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，如果∠ABP＝20°，∠ACP＝50°，则∠A+∠P＝（ ）
A．70°B．80°C．90°D．100°
【分析】根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和，可求出∠A的度数，根据补角的定义求出∠ACB的度数，根据三角形的内角和即可求出∠P的度数，即可求出结果．
【解析】∵BP是△ABC中∠ABC的平分线，CP是∠ACB的外角的平分线，
∵∠ABP＝20°，∠ACP＝50°，
∴∠ABC＝2∠ABP＝40°，∠ACM＝2∠ACP＝100°，
∴∠A＝∠ACM﹣∠ABC＝60°，
∠ACB＝180°﹣∠ACM＝80°，
∴∠BCP＝∠ACB+∠ACP＝130°，
∵∠PBC＝20°，
∴∠P＝180°﹣∠PBC﹣∠BCP＝30°，
∴∠A+∠P＝90°，
故选：C．
28．（2020秋•仓山区期末）如图，△ABC中，AC＝BC，过点B作射线BF，在射线BF上取一点E，使得∠CBF＝∠CAE，过点C作射线BF的垂线，垂足为点D，连接AE，若DE＝a，AE＝b，则BD的长度为（ ）
A．bB．a+bC．12a+bD．2a+b
【分析】如图，连接CE，过点C作CM⊥AE交AE于M，利用全等三角形的性质证明BD＝AM，DE＝EM即可解决问题．
【解析】如图，连接CE，过点C作CM⊥AE交AE于M．
∵CD⊥BF，CM⊥AM，
∴∠CDB＝∠M＝90°，
在△CDB△CMA中，
∠CDB=∠M∠CBD=∠CAMCB=AC，
∴△CDB≌△CMA（AAS），
∴CM＝CD，BD＝AM，
在Rt△CED和Rt△CEM，
CE=CECD=CM，
∴Rt△CED≌Rt△CEM（HL），
∴DE＝EM＝a，
∴BD＝AM＝AE+EM＝AE+DE＝a+b，
故选：B．
29．（2020秋•仓山区期末）某木材市场上木棒规格与对应价格如下表：
小明的爷爷要做一个三角形木架养鱼用，现有两根长度分别为3m和5m的木棒，还需要到该木材市场购买一根木棒．则小明的爷爷至少带的钱数应为（ ）
A．10B．15C．20D．25
【分析】根据三角形的三边关系可得5﹣2＜x＜5+2，再解出不等式可得x的取值范围，进而得到选择的木棒长度，然后根据木棒价格可直接选出答案．
【解析】设第三根木棒的长度为xm，
根据三角形的三边关系可得：5﹣2＜x＜5+2，
解得2＜x＜8，
x＝3，4，5，6，7，共5种选择，
根据木棒的价格可得选3m最省钱，
所以小明的爷爷至少带的钱数应为20元，
故选：C．
30．（2020秋•苏州期末）如图，在长方形ABCD中，AB＝6cm，BC＝8cm，点E是AB上的一点，且AE＝2BE．点P从点C出发，以2cm/s的速度沿点C﹣D﹣A﹣E匀速运动，最终到达点E．设点P运动时间为ts，若三角形PCE的面积为18cm2，则t的值为（ ）
A．98或194B．98或194或274
C．94或6D．94或6或274
【分析】分下列三种情况讨论，如图1，当点P在CD上，即0＜t≤3时，根据三角形的面积公式建立方程求出其解即可；如图2，当点P在AD上，即3＜t≤7时，由S△PCE＝S四边形AECD﹣S△PCD﹣S△PAE建立方程求出其解即可；如图3，当点P在AE上，即7＜t≤9时，由S△PCE=12PE•BC＝18建立方程求出其解即可．
【解析】如图1，当点P在CD上，即0＜t≤3时，
∵四边形ABCD是矩形，
∴AB＝CD＝6cm，AD＝BC＝8cm．
∵CP＝2t（cm），
∴S△PCE=12×2t×8＝18，
∴t=94；
如图2，当点P在AD上，即3＜t≤7时，
∵AE＝2BE，
∴AE=23AB＝4．
∵DP＝2t﹣6，AP＝8﹣（2t﹣6）＝14﹣2t．
∴S△PCE=12×（4+6）×8-12（2t﹣6）×6-12（14﹣2t）×4＝18，
解得：t＝6；
当点P在AE上，即7＜t≤9时，
PE＝18﹣2t．
∴S△APE=12（18﹣2t）×8＝18，
解得：t=274＜7（舍去）．
综上所述，当t=94或6时△APE的面积会等于18．
故选：C．

规格
1m
2m
3m
4m
5m
6m
价格（元/根）
10
15
20
25
30
35