专题4.7小题能力提升考前必做30题（压轴篇）-2021-2022学年七年级数学下学期期中考试高分直通车【北师大版】

这是一份专题4.7小题能力提升考前必做30题（压轴篇）-2021-2022学年七年级数学下学期期中考试高分直通车【北师大版】，文件包含专题47小题能力提升考前必做30题压轴篇-2021-2022学年七年级数学下学期期中考试高分直通车解析版北师大版docx、专题47小题能力提升考前必做30题压轴篇-2021-2022学年七年级数学下学期期中考试高分直通车原卷版北师大版docx等2份试卷配套教学资源，其中试卷共23页， 欢迎下载使用。

2021-2022学年七年级下学期期中考试高分直通车（北师大版）
专题4.7小题能力提升考前必做30题（压轴篇）
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷试题共30题，选择15道、填空15道.答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一．选择题（共15小题）
1．（2020秋•邓州市期中）如图，将图①中大小相同的四个小正方形按图②所示的方式放置变为一个大正方形，根据两个图形中阴影部分的面积关系，可以验证（　　）

A．（a﹣b）2＝a2﹣2ab+b2 B．（a+b）2＝a2+2ab+b2
C．（a﹣b）2＝（a+b）2﹣4ab D．（a+b）（a﹣b）＝a2﹣b2
【分析】根据图形阴影部分的面积的不同求法可得等式．
【解析】阴影部分的面积是四个阴影小正方形的面积和，由拼图可得四个阴影小正方形可以拼成边长为（a﹣b）的正方形，因此面积为（a﹣b）2，
由图2可知，阴影部分的面积等于边长为a的正方形的面积减去之间十字架的面积，即：a2﹣2ab+b2，
因此有（a﹣b）2＝a2﹣2ab+b2，
故选：A．
2．（2020春•槐荫区期中）若a+b＝10，ab＝11，则代数式a2﹣ab+b2的值是（　　）
A．89 B．﹣89 C．67 D．﹣67
【分析】把a+b＝10两边平方，利用完全平方公式化简，将ab＝11代入求出a2+b2的值，代入原式计算即可得到结果．
【解析】把a+b＝10两边平方得：
（a+b）2＝a2+b2+2ab＝100，
把ab＝11代入得：
a2+b2＝78，
∴原式＝78﹣11＝67，
故选：C．
3．（2019春•青羊区校级期中）形如abcd的式子叫做二阶行列式，它的算法是：abcd=ad﹣bc，则aa-2a+2a+1的运算结果是（　　）
A．a+4 B．a﹣4 C．4 D．﹣4
【分析】先得出算式，再根据整式的乘法法则算乘法，最后合并同类项即可．
【解析】aa-2a+2a+1
＝a（a+1）﹣（a+2）（a﹣2）
＝a2+a﹣a2+4
＝a+4，
故选：A．
4．（2019春•新田县期中）若A=-23（1+131）（1+132）（1+134）（1+138）（1+1316）（1+1332）（1+1364）…（1+132n）+1，则A的值是（　　）
A．0 B．1 C．1322n D．132n+1
【分析】先将-23变形为：﹣（1-13），再利用平方差公式化简即可．
【解析】A=-23（1+131）（1+132）（1+134）（1+138）（1+1316）（1+1332）（1+1364）……（1+132n）+1
＝﹣（1-13）（1+131）（1+132）（1+134）（1+138）（1+1316）（1+1332）（1+1364）……（1+132n）+1
＝﹣（1-132）（1+132）（1+134）（1+138）（1+1316）（1+1332）（1+1364）……（1+132n）+1
＝﹣（1-132n）（1+132n）+1
＝﹣（1-132n+1）+1
=132n+1
故选：D．
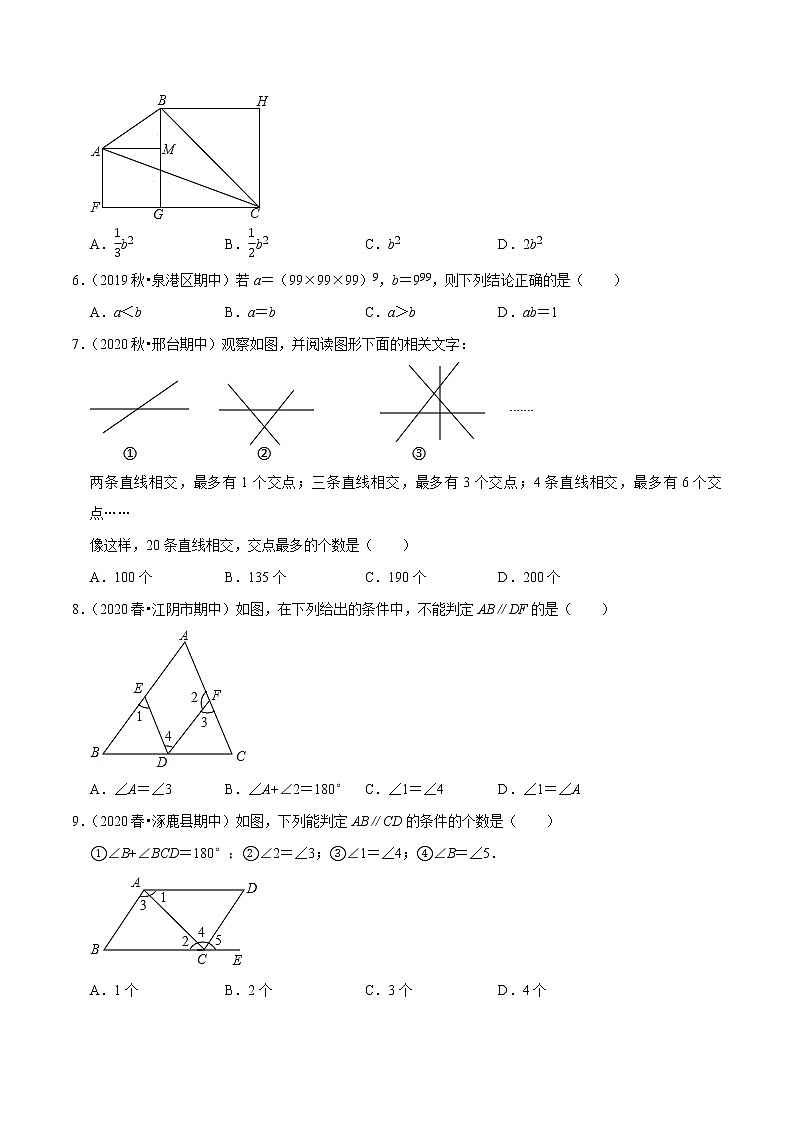
5．（2019秋•合浦县期中）如图．将面积为a2的小正方形与面积为b2的大正方形放在一起（a＞0，b＞0）则三角形ABC的面积是（　　）

A．13b2 B．12b2 C．b2 D．2b2
【分析】根据图形得出三角形ABC的面积S＝正方形AFGM+S正方形BGCH+S△AMB﹣S△AFC﹣S△BHC，再根据面积公式求出即可．
【解析】∵将面积为a2的小正方形与面积为b2的大正方形放在一起，
∴CM＝AF＝FG＝a，BG＝CG＝CH＝BH＝b，
∴三角形ABC的面积S＝正方形AFGM+S正方形BGCH+S△AMB﹣S△AFC﹣S△BHC
＝a2+b2+12⋅a•（b﹣a）-12⋅a•（a+b）-12⋅b•b
＝a2+b2+12ab-12a2-12a2-12ab-12b2
=12b2，
故选：B．
6．（2019秋•泉港区期中）若a＝（99×99×99）9，b＝999，则下列结论正确的是（　　）
A．a＜b B．a＝b C．a＞b D．ab＝1
【分析】由于a和b均大于1，故可排除D；计算ab，根据其值与1的大小即可判断a和b的大小．
【解析】∵a＝（99×99×99）9，b＝999，两个数均大于1
∴D选项：ab＝1错误；
∵ab=(99×99×99)9999=9927999=1127972=(119)27•1945
∵1＜(119)27＜227＜945
∴0＜(119)27•1945＜1
∴0＜ab＜1
∴a＜b
∴选项B，C不正确．
故选：A．
7．（2020秋•邢台期中）观察如图，并阅读图形下面的相关文字：

两条直线相交，最多有1个交点；三条直线相交，最多有3个交点；4条直线相交，最多有6个交点……
像这样，20条直线相交，交点最多的个数是（　　）
A．100个 B．135个 C．190个 D．200个
【分析】根据题意，结合图形，发现：3条直线相交最多有3个交点，4条直线相交最多有6个交点，5条直线相交最多有10个交点，故可猜想，n条直线相交，最多有1+2+3+…+（n﹣1）=12n（n﹣1）个交点，据此解答即可．
【解析】2条直线相交最多有1个交点，1=12×1×2，
3条直线相交最多有3个交点，3＝1+2=12×2×3，
4条直线相交最多有6个交点，6＝1+2+3=12×3×4，
5条直线相交最多有10个交点，10＝1+2+3+4=12×4×5，
…
n条直线相交最多有交点的个数是：12n（n﹣1）．
20条直线相交最多有交点的个数是：12n（n﹣1）=12×20×19＝190．
故选：C．
8．（2020春•江阴市期中）如图，在下列给出的条件中，不能判定AB∥DF的是（　　）

A．∠A＝∠3 B．∠A+∠2＝180° C．∠1＝∠4 D．∠1＝∠A
【分析】利用平行线的判定定理，逐一判断，容易得出结论．
【解析】A、因为∠A＝∠3，所以AB∥DF（同位角相等，两直线平行），故本选项不符合题意．
B、因为∠A+∠2＝180，所以AB∥DF（同旁内角互补，两直线平行），故本选项不符合题意．
C、因为∠1＝∠4，所以AB∥DF（内错角相等，两直线平行），故本选项不符合题意．
D、因为∠1＝∠A，所以AC∥DE（同位角相等，两直线平行），不能证出AB∥DF，故本选项符合题意．
故选：D．
9．（2020春•涿鹿县期中）如图，下列能判定AB∥CD的条件的个数是（　　）
①∠B+∠BCD＝180°；②∠2＝∠3；③∠1＝∠4；④∠B＝∠5．

A．1个 B．2个 C．3个 D．4个
【分析】根据平行线的判定定理分别进行判断即可．
【解析】当∠B+∠BCD＝180°，AB∥CD；当∠3＝∠2时，AB＝BC；当∠1＝∠4时，AD＝DC；当∠B＝∠5时，AB∥CD．
故选：B．
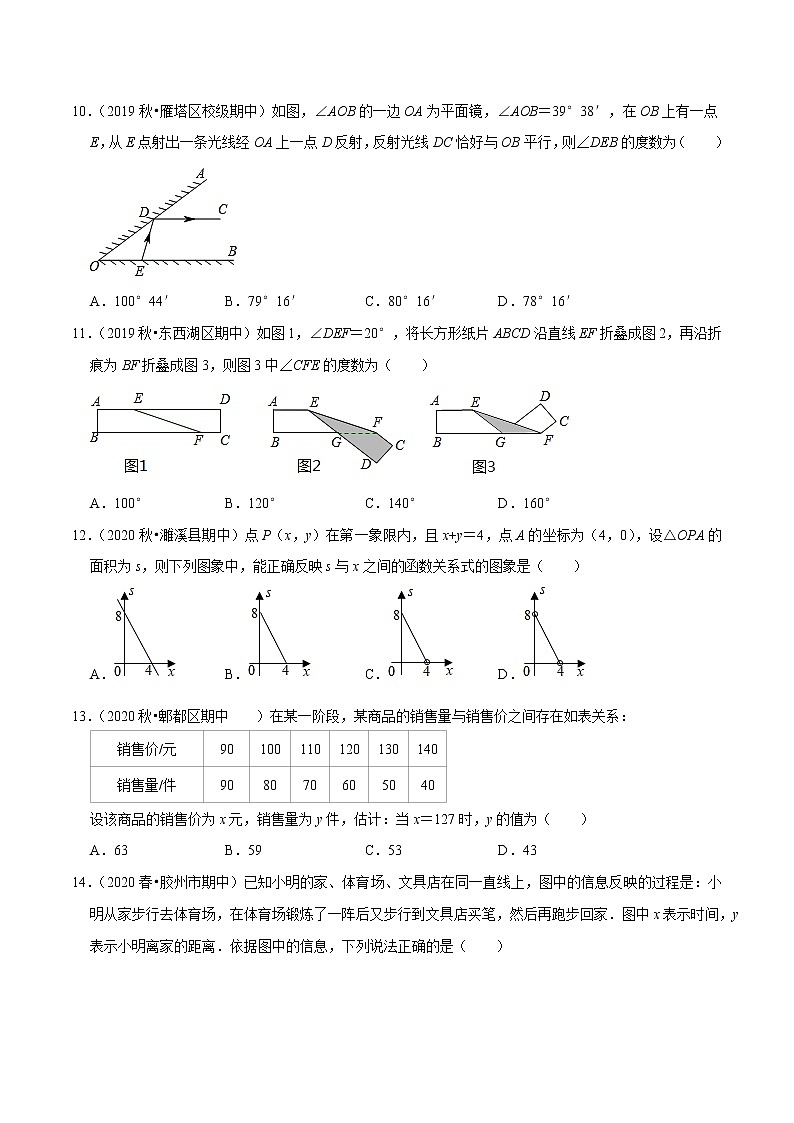
10．（2019秋•雁塔区校级期中）如图，∠AOB的一边OA为平面镜，∠AOB＝39°38′，在OB上有一点E，从E点射出一条光线经OA上一点D反射，反射光线DC恰好与OB平行，则∠DEB的度数为（　　）

A．100°44′ B．79°16′ C．80°16′ D．78°16′
【分析】利用平行线的性质以及光的反射定理解决问题即可．
【解析】∵CD∥OB，
∴∠ADC＝∠AOB＝39°38′，
∵∠ADC＝∠ODE＝39°38′，
∴∠DEB＝∠AOB+∠ODE＝79°16′，
故选：B．
11．（2019秋•东西湖区期中）如图1，∠DEF＝20°，将长方形纸片ABCD沿直线EF折叠成图2，再沿折痕为BF折叠成图3，则图3中∠CFE的度数为（　　）

A．100° B．120° C．140° D．160°
【分析】根据两直线平行，同旁内角互补可得∠CFE＝180°﹣∠DEF，然后得出图2中∠CFE度数；再根据两直线平行，内错角相等可得∠BFE＝∠DEF，然后求出图2中∠BFC，再根据翻折的性质可得∠CFE+∠BFE＝∠BFC，然后代入数据计算即可得解．
【解析】∵矩形对边AD∥BC，
∴CF∥DE，
∴图1中，∠CFE＝180°﹣∠DEF＝180°﹣20°＝160°，
∵矩形对边AD∥BC，
∴∠BFE＝∠DEF＝20°，
∴图2中，∠BFC＝160°﹣20°＝140°，
由翻折的性质得，图3中∠CFE+∠BFE＝∠BFC，
∴图3中，∠CFE+20°＝140°，
∴图3中，∠CFE＝120°，
故选：B．
12．（2020秋•濉溪县期中）点P（x，y）在第一象限内，且x+y＝4，点A的坐标为（4，0），设△OPA的面积为s，则下列图象中，能正确反映s与x之间的函数关系式的图象是（　　）
A． B． C． D．
【分析】先用x表示出y，再利用三角形的面积公式即可得出结论．
【解析】∵点P（x，y）在第一象限内，且x+y＝4，
∴y＝4﹣x（0＜x＜4，0＜y＜4）．
∵点A的坐标为（4，0），
∴S=12×4×（4﹣x）＝﹣2x+8，
∵0＜x＜4，故0＜S＜8，
∴D符合．
故选：D．
13．（2020秋•郫都区期中）在某一阶段，某商品的销售量与销售价之间存在如表关系：
销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元，销售量为y件，估计：当x＝127时，y的值为（　　）
A．63 B．59 C．53 D．43
【分析】该商品的销售价每增加10元，销售量就减少10件，所以可以分析出销售量y与销售价x符合一次函数关系，再设出函数解析式，代入表格中的数据求出解析式，再把x＝127代入求y的值即可．
【解析】由图表可以看出y与x符合一次函数关系，设y＝kx+b（k≠0），
把x＝90，y＝90和x＝100，y＝80代入得，
90k+b=90100k+b=80，
解得：k=-1b=180，
则y＝﹣x+180，
当x＝127时，y＝﹣127+180＝53．
故选：C．
14．（2020春•胶州市期中）已知小明的家、体育场、文具店在同一直线上，图中的信息反映的过程是：小明从家步行去体育场，在体育场锻炼了一阵后又步行到文具店买笔，然后再跑步回家．图中x表示时间，y表示小明离家的距离．依据图中的信息，下列说法正确的是（　　）

A．体育场离小明家1.5 km
B．小明在体育场锻炼时间为40min
C．小明从家到体育场时步行的平均速度是0.1 m/min
D．小明从文具店跑步回家的平均速度是300 m/min
【分析】利用函数图象中横、纵坐标的意义分别求解．
【解析】A、体育场离小明家1km，选项错误，不符合题意；
B、小明在体育场锻炼时间为40﹣10＝30min，选项错误，不符合题意；
C、小明从家到体育场时步行的平均速度是110=0.1km/min，选项错误，不符合题意；
D、小明从文具店跑步回家的平均速度是150055-50=300 m/min，选项正确，符合题意；
故选：D．
15．（2019春•杏花岭区校级期中）甲、乙两人沿相同路线前往距离单位10km的培训中心参加学习．图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S（千米）随时间t（分）两个变量之间关系的图象．以下说法：①乙比甲提前12分钟到达；②甲的平均速度为15千米/小时；③乙走了8km后遇到甲．其中正确的有（　　）

A．3个 B．2个 C．1个 D．0个
【分析】观察函数图象可知，函数的横坐标表示时间，纵坐标表示路程，然后根据图象上特殊点的意义进行解答．
【解析】①乙在28（分）时到达，甲在40（分）时到达，所以乙比甲提前了12分钟到达；故①正确；
②根据甲到达目的地时的路程和时间知：甲的平均速度=10÷4060=15千米/时；故②正确；
③设乙出发x分钟后追上甲，则有：1028-18×x=1040×(18+x)，解得x＝6，
乙第一次遇到甲时，所走的距离为：6×1028-18=6km，故③错误；
所以正确的结论有两个：①②
故选：B．
二．填空题（共15小题）
16．（2020秋•兴庆区校级期中）某市出租车白天的收费起步价为7元，即路程不超过3千米时收费7元，超过部分每千米收费1.2元，如果乘客白天乘坐出租车的路程为x（x＞3）千米，乘车费为y元，那么y与x之间的关系为　y＝1.2x+3.4　．
【分析】根据乘车费用＝起步价+超过3千米的费用即可得出．
【解析】依据题意得：y＝7+1.2（x﹣3）＝1.2x+3.4，
故答案为：y＝1.2x+3.4，
17．（2020秋•万州区校级期中）一辆轿车和一辆货车同时从甲地出发驶往乙地，轿车到达乙地后立即以另一速度原路返回甲地，货车到达乙地后停止．如图所示的图象分别表示货车、轿车离甲地的距离（千米）与轿车所用时间（小时）的关系．当轿车从乙地返回甲地的途中与货车相遇时，相遇处离甲地的距离为　75　千米．

【分析】根据函数图象中的数据，可以计算出货车的速度已经轿车返回时的速度，然后即可计算出相遇处到甲地的距离．
【解析】由图象可得，货车的速度为：90÷2＝45（千米/小时），
轿车返回时的速度为：90÷（2.5﹣1.5）＝90（千米/小时），
设当轿车从乙地返回甲地的途中与货车相遇时，货车行驶的时间为a小时，
45a+90（a﹣1.5）＝90，
解得，a=53，
45×53=75（千米），
即相遇处到甲地的距离是75千米．
故答案为：75．
18．（2019秋•苏州期中）如图①，把一个长为16厘米、宽为4厘米的长方形从正方形的左边平移到右边，每秒平移2厘米，图②是长方形在平移过程中与正方形重叠部分的面积与平移时间的关系图，根据图中信息可得t1+t2＝　14　秒．

【分析】当长方形的右侧和正方形的右侧重合时，此时的时间为t1，则48＝4×2t1，则t1＝6，则正方形的边长为4，则长方形在正方形内运动2秒，即可求解．
【解析】当长方形的右侧和正方形的右侧重合时，此时的时间为t1，
则48＝4×2t1，则t1＝6，
则正方形的边长为4，则长方形在正方形内运动2秒，重叠的面积开始减小，故t2＝t1+2＝8，
故t1+t2＝14（秒），
故答案为14．
19．（2020春•高新区期中）如图，若AB∥CD，BF平分∠ABE，DF平分∠CDE，∠BED＝90°，则∠BFD＝　45°　．

【分析】根据平行线的性质和角平分线的性质，可以求得∠BFD的度数，本题得以解决．
【解析】∵AB∥CD，
∴∠ABE＝∠4，∠1＝∠2，
∵∠BED＝90°，∠BED＝∠4+∠EDC，
∴∠ABE+∠EDC＝90°，
∵BF平分∠ABE，DF平分∠CDE，
∴∠1+∠3＝45°，
∵∠5＝∠2+∠3，
∴∠5＝∠1+∠3＝45°，
即∠BFD＝45°，
故答案为：45°．

20．（2020春•黄岛区期中）如图，已知AB∥DE，∠ABC＝76°，∠CDE＝150°，则∠BCD的度数为　46　°．

【分析】根据平行线的性质，可以求得∠BCF和∠DCF的度数，从而可以得到∠BCD的度数．
【解析】过点C作CF∥AB，
∵AB∥DE，
∴AB∥DE∥CF，
∴∠ABC＝∠BCF，∠CDE+∠DCF＝180°，
∵∠ABC＝76°，∠CDE＝150°，
∴∠BCF＝76°，∠DCF＝30°，
∴∠BCD＝46°，
故答案为：46．

21．（2020春•成华区校级期中）如图，如果AB∥CD，则角α＝130°，γ＝20°，则β＝　70°　．

【分析】过点E作EF∥AB，根据AB∥CD，可得AB∥CD∥EF，根据平行线的性质即可求出β的度数．
【解析】如图，过点E作EF∥AB，

∵AB∥CD，
∴AB∥CD∥EF，
∴∠A+∠AEF＝180°，∠D＝∠FED，
∴∠AEF＝180°﹣130°＝50°，∠FED＝20°，
∴∠AED＝∠AEF+∠FED＝50°+20°＝70°．
即β＝70°．
故答案为：70°．
22．（2020春•越城区校级期中）如图，∠AOB＝60°，在∠AOB的内部有一点P，以P为顶点，作∠CPD，使∠CPD的两边与∠AOB的两边分别平行，∠CPD的度数为　60或120　度．

【分析】先根据题意画出图形，再根据平行线的性质得出即可．
【解析】如图MN∥OB，EF∥OA，
分为两种情况：①当∠CPD＝∠MPF（或∠EPN）时，
∠CPD＝∠AOB＝60°；
②当∠CPD＝∠MPE（或∠FPN）时，∠CPD＝180°﹣∠AOB＝120°，
故答案为：60或120．
23．（2020春•顺城区校级期中）如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC＝115°，∠ACF＝25°，则∠FEC＝　20　度．

【分析】根据两直线平行，同旁内角互补求出∠ACB，再求出∠BCF，然后根据角平分线的定义求出∠BCE，再利用两直线平行，内错角相等可得∠FEC＝∠BCE．
【解析】∵AD∥BC，
∴∠ACB＝180°﹣∠DAC＝180°﹣115°＝65°，
∵∠ACF＝25°，
∴∠BCF＝∠ACB﹣∠ACF＝65°﹣25°＝40°，
∵CE平分∠BCF，
∴∠BCE=12∠BCF=12×40°＝20°，
∵EF∥AD，AD∥BC，
∴EF∥BC，
∴∠FEC＝∠BCE＝20°．
故答案为：20．
24．（2020春•赣州期中）已知线段AB与直线CD互相垂直，垂足为点O，且AO＝5cm，BO＝3cm，则线段AB的长为　8cm或2cm　．
【分析】考虑点O在线段AB内、外两种情况进行解答．
【解析】当点O在线段AB内时，AB＝AO+BO＝5cm+3cm＝8cm，
当点O在线段AB外时，AB＝AO﹣BO＝5cm﹣3cm＝2cm．

故答案为：8cm 或2cm．
25．（2020春•奉化区期中）若a4+b4＝a2﹣2a2b2+b2+20，则a2+b2＝　5　．
【分析】将a2+b2看成整体，作为未知数，经过变形得到它的方程即可求解；需注意a2+b2不能是负数．
【解析】由已知a4+b4＝a2﹣2a2b2+b2+20得：
a4+2a2b2+b4﹣a2﹣b2﹣20＝0，
（a2+b2）2﹣（a2+b2）﹣20＝0，
∴（a2+b2﹣5）（a2+b2+4）＝0，
∴a2+b2＝5或a2+b2＝﹣4；
而a2+b2≥0，故a2+b2＝﹣4舍去，
∴a2+b2＝5，
故答案为5．
26．（2020秋•武侯区校级期中）对于代数式4x2﹣12x+11，利用完全平方公式，可求其最小值是　2　．
【分析】将原式配方后，利用非负数的性质确定出最小值即可．
【解析】4x2﹣12x+11
＝4（x2﹣3x）+11
＝4（x2﹣3x+94-94）+11
＝4（x-32）2+2，
则代数式4x2﹣12x+11的最小值是2．
故答案为：2．
27．（2020秋•武侯区校级期中）若（x+2）（x+a）＝x2+bx﹣8，则ab的值为　116　．
【分析】先计算等号左边，再根据等式求出a、b的值，最后代入求出ab的值．
【解析】∵（x+2）（x+a）＝x2+（2+a）x+2a，
又∵（x+2）（x+a）＝x2+bx﹣8，
∴x2+（2+a）x+2a＝x2+bx﹣8．
∴2+a＝b，2a＝﹣8．
∴a＝﹣4，b＝﹣2．
∴ab＝（﹣4）﹣2
=1(-4)2
=116．
故答案为：116．
28．（2020秋•慈溪市期中）如图，将边长为a的正方形剪去两个小长方形得到S图案，再将这两个小长方形拼成一个新的长方形，求新的长方形的周长　4a﹣8b　．

【分析】先根据题意列出算式，再根据整式的运算法则进行化简即可．
【解析】新长方形的周长是2（a﹣3b）+2（a﹣b）＝2a﹣6b+2a﹣2b＝4a﹣8b，
故答案为：4a﹣8b．
29．（2020秋•海淀区校级期中）下列有四个结论．其中正确的是　②④　．
①若（x﹣1）x+1＝1，则x只能是2；
②若（x﹣1）（x2+ax+1）的运算结果中不含x2项，则a＝1；
③若a+b＝10，ab＝2，则a﹣b＝2；
④若4x＝a，8y＝b，则23y﹣2x可表示ba．
【分析】根据多项式乘多项式、幂的乘方、同底数幂除法、零指数幂等逐一进行计算即可．
【解析】①若（x﹣1）x+1＝1，则x是2或﹣1．故①错误；
②若（x﹣1）（x2+ax+1）的运算结果中不含x2项，
∵（x﹣1）（x2+ax+1）＝x3+（a﹣1）x2+（1﹣a）x﹣1，
∴a﹣1＝0，解得a＝1，故②正确；
③若a+b＝10，ab＝2，
∵（a﹣b）2＝（a+b）2﹣4ab＝100﹣8＝92，
则a﹣b＝223，故③错误；
④若4x＝a，8y＝b，则23y﹣2x＝（23）y÷（22）x＝8y÷4x=ba．故④正确．
所以其中正确的是②④．
故答案为：②④．
30．（2020春•文登区期末）有两个正方形A、B，现将B放在A的内部得图甲，将A、B并列放置后构造新的正方形得图乙，若图甲和图乙中阴影部分的面积分别为2和20，则正方形A、B的面积之和为　22　．

【分析】设正方形A的边长为a，正方形B的边长为b，由图形得出关系式求解即可．
【解析】设正方形A的边长为a，正方形B的边长为b，
由图甲得a2﹣b2﹣2（a﹣b）b＝2，即a2+b2﹣2ab＝2，
由图乙得（a+b）2﹣a2﹣b2＝20，2ab＝20，
所以a2+b2＝22，
故答案为：22．