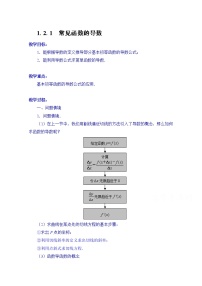
高中人教版新课标B1.2.1常数函数与幂函数的导数教案

这是一份高中人教版新课标B1.2.1常数函数与幂函数的导数教案，共5页。

教学目标：
1．由定义求导数的三个步骤推导五种常见函数的导数公式；
2．掌握并能运用这五个公式正确求函数的导数．
教学重点：
五种常见函数的导数公式及应用
教学难点：
五种常见函数导数公式的推导
教学过程：
一．课题导入
我们知道，导数的几何意义是曲线在某一点处的切线斜率，物理意义是运动物体在某一时刻的瞬时速度．那么，对于函数，如何求它的导数呢？
由导数定义本身，给出了求导数的最基本的方法，但这种方法在运算上很麻烦，有时甚至很困难，为了能够较快地求出某些函数的导数，从这一节课开始我们将研究比较简捷的求导数的方法，下面我们先求几个常用的函数的导数．
二．新课讲授
1．函数的导数
根据导数定义，因为
所以
表示函数图像（图1.2-1）上每一点处的切线的斜率都为0．若表示路程关于时间的函数，则可以解释为某物体的瞬时速度始终为0，即物体一直处于静止状态．
2．函数的导数
因为
所以
表示函数图像（图1.2-2）上每一点处的切线的斜率都为1．若表示路程关于时间的函数，则可以解释为某物体做瞬时速度为1的匀速运动．
练习：在同一直角坐标系中，分别画出函数,,的图象，求出它们的导数。
（1）从图象上看，它们的导数分别表示什么?
（2）这三个函数，哪一个增加得最快，哪一个增加的最慢？
（3）函数增（减）的快慢与什么有关？
3．函数的导数
因为
所以
表示函数图像（图1.2-3）上点处的切线的斜率都为，说明随着的变化，切线的斜率也在变化．另一方面，从导数作为函数在一点的瞬时变化率来看，表明：当时，随着的增加，函数减少得越来越慢；当时，随着的增加，函数增加得越来越快．若表示路程关于时间的函数，则可以解释为某物体做变速运动，它在时刻的瞬时速度为．
4．函数的导数
因为
所以
练习 作出函数的图象，根据图象，描述它的变化情况，并求出其在点（1，1）处的切线方程
5．函数的导数
因为
=
=
所以
6.推广：若，则
练习 求下列函数的导数
（1）（2）
（3）（4）
三．例题讲解
例1．曲线上哪一点的切线与直线平行？
解：设点为所求，则
它的切线斜率为，
∵，
∴，，
∴或．
例2．证明：曲线上的任何一点的切线与两坐标轴围成的三角形面积是一个常数．
解：由，得，
∴，
∴，
过点的切线方程为
，
令得，
令得，
∴过的切线与两坐标轴围成的三角形面积
是一个常数．
四．课时小结
，
五．布置作业
红对勾第四课时

板书设计
1.2.1 几个常用函数的导数
公式1：(C为常数)


公式2：
例1
例2