专题07 实数知识讲解 2022年七年级数学寒假辅导讲义

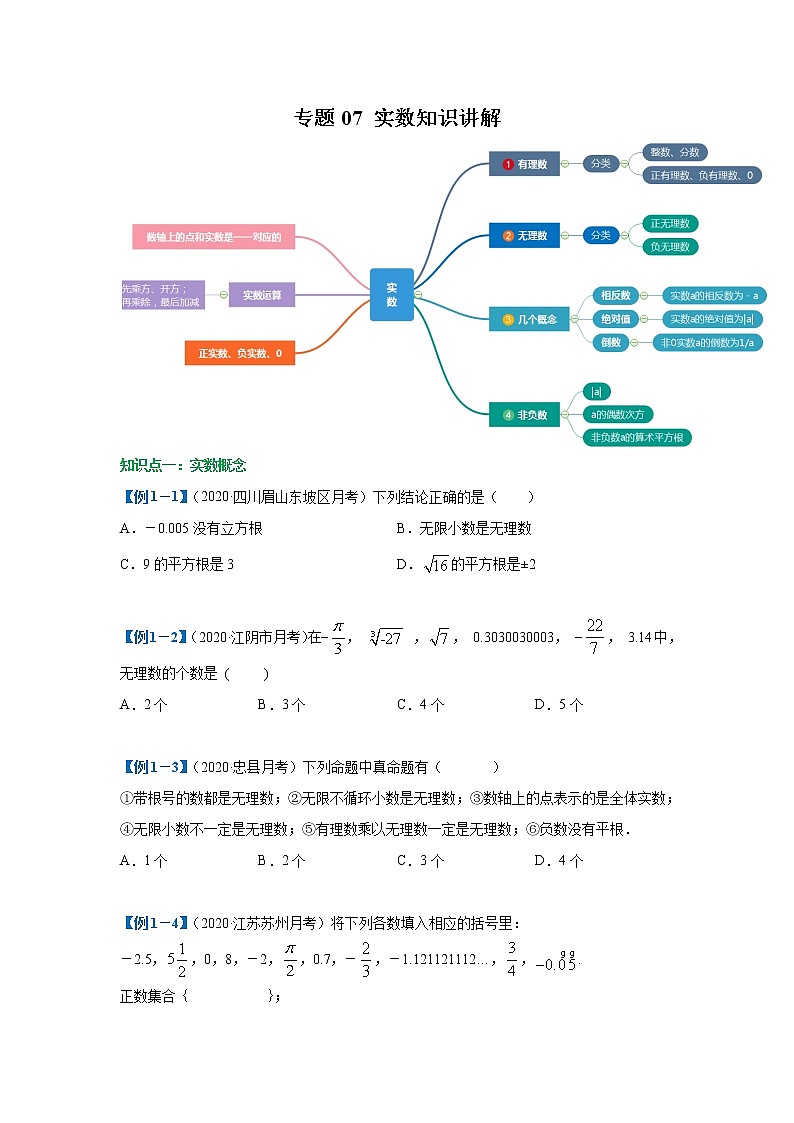
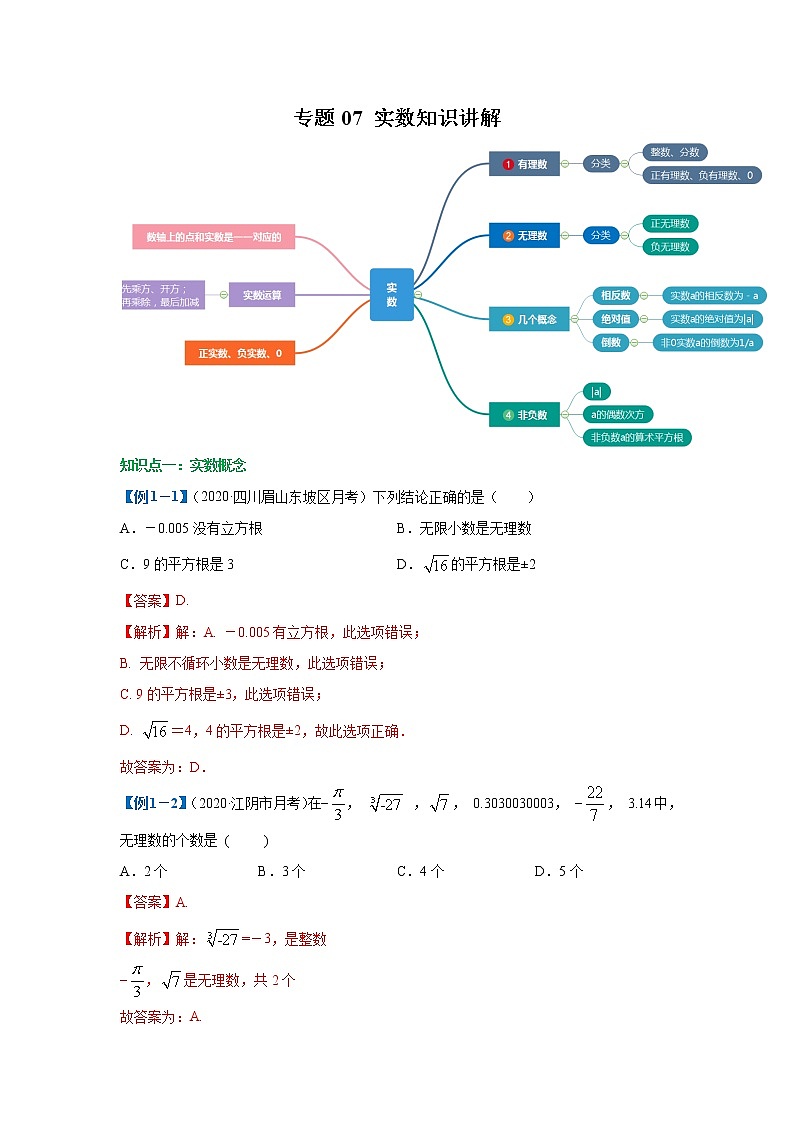
专题07 实数知识讲解

知识点一：实数概念
【例1－1】（2020·四川眉山东坡区月考）下列结论正确的是（ ）
A．－0.005没有立方根 B．无限小数是无理数
C．9的平方根是3 D．的平方根是±2
【答案】D.
【解析】解：A. －0.005有立方根，此选项错误；
B. 无限不循环小数是无理数，此选项错误；
C. 9的平方根是±3，此选项错误；
D. ＝4，4的平方根是±2，故此选项正确．
故答案为：D．
【例1－2】（2020·江阴市月考）在−， ，， 0.3030030003， −， 3.14中，无理数的个数是 ( )
A．2个 B．3个 C．4个 D．5个
【答案】A.
【解析】解：=－3，是整数
−，是无理数，共2个
故答案为：A.
【例1－3】（2020·忠县月考）下列命题中真命题有（ ）
①带根号的数都是无理数；②无限不循环小数是无理数；③数轴上的点表示的是全体实数；
④无限小数不一定是无理数；⑤有理数乘以无理数一定是无理数；⑥负数没有平根．
A．1个 B．2个 C．3个 D．4个
【答案】D.
【解析】解：①带根号的数不一定是无理数，如=2，是假命题；
②无限不循环小数是无理数，是真命题；
③实数与数轴上的点是一一对应，是真命题；
④无限小数不一定是无理数，如无限循环小数是有理数，真命题；
⑤有理数乘以无理数一定是无理数，如0×π=0，假命题；
⑥负数没有平方根，真命题．
故答案为：D.
【例1－4】（2020·江苏苏州月考）将下列各数填入相应的括号里：
－2.5，，0，8，－2，，0.7，－，－1.121121112…，，.
正数集合｛ ｝；
负数集合｛ ｝；
整数集合｛ ｝；
有理数集合｛ ｝；
无理数集合｛ ｝.
【答案】见解析.
【解析】解：正数集合， 8，，， …；
负数集合，，，…，． …；
整数集合，8，， … ；
有理数集合，，，8，， ，， ，．…；
无理数集合，…， ….
【变式1－1】（2020·沈阳市月考）在 0，0.2，3π，，6.1010010001…（相邻两个1之间0的个数逐次加1），，中，无理数有（　　）个．
A．2个 B．3个 C．4个 D．5个
【答案】B.
【解析】解：0，0.2，，是有理数，
3π，6.1010010001…（相邻两个1之间0的个数逐次加1），是无理数，
故答案为：B．
【变式1－2】（2020·唐河县月考）下列命题中，假命题的个数是（ ）
①无限小数是无理数
②从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离
③平行于同一条直线的两条直线平行
④过一点有且只有一条直线与已知直线垂直
A．1个 B．2个 C．3个 D．4个
【答案】C.
【解析】解：①无限不循环小数是无理数，故原命题错误，是假命题；
②从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离，故原命题错误，；
③平行于同一条直线的两条直线平行，正确，是真命题；
④在同一平面内，过一点有且只有一条直线与已知直线垂直，故原命题错误，是假命题
∴假命题有3个；
故答案为：C．
【变式1－3】（2020·山东菏泽月考）把下列各数填在相应的表示集合的括号内．
－1，－，，0，，－0．303303330…, 1.7 ，－(－2)，2π．
整数集合： （____________________________________）……）
正分数集合：（___________________________________）……）
无理数集合：（___________________________________）……）
【答案】见解析.
【解析】解：整数集合：{－1，－|－3|，0，－(－2)}
正分数集合：{，1.7}
无理数集合：{－0.303303330…，2π}
知识点二：实数运算
【例2－1】（2020·黑龙江哈尔滨期末）计算：
（1）
（2）
【答案】（1）；（2）－2.05．
【解析】解：（1）原式
．
（2）原式=0.2－2－0.25
=－2.05
【变式2－1】计算（1）
（2）
【答案】（1）3.5；（2）.
【解析】解：
（1）原式=5－3+1.5
=3.5
（2）原式，
．
【例3－1】（2020·河南洛阳月考）请先在草稿纸上计算下列四个式子的值：①；②；③；④．观察计算的结果，由发现的规律得出的值为（　　）
A．351 B．350 C．325 D．300
【答案】C.
【解析】解：
①＝1；
②＝3＝1+2；
③＝6＝1+2+3；
④＝10＝1+2+3+4；
∴
＝1+2+3+…+25
＝325．
故答案为：C．
【变式3－1】（2020·山西朔州期中）各个数位上数字的立方和等于其本身的三位数叫做“水仙花数”．例如153是“水仙花数”，因为．以下四个数中是“水仙花数”的是（ ）
A．135 B．220 C．345 D．407
【答案】D.
【解析】解：，不是“水仙花数”；
，不是“水仙花数”；
，不是“水仙花数”；
，是“水仙花数”；
故答案为：D ．
【变式3－2】（2021·四川省遂宁月考）现规定一种运算：ab＝ab＋a－b，其中a，b为实数，则____．
【答案】－2.
【解析】解：∵a※b＝ab＋a－b，
∴
=4×(－2)+4－(－2)
=－8+4+2
=－2．
故答案为：－2．
【变式3－3】（2020·无锡市月考）在一列数：，，，…，中，，从第三个数开始，每一个数都等于它前两个数之积的个位数字，则这列数中的第2020个数是（ ）
A．1 B．3 C．7 D．9
【答案】C.
【解析】解：由题意可得：
a1＝7，a2＝1，a3＝7，a4＝7，a5＝9， a6＝3，
a7＝7，a8＝1，…，
∵2020÷6＝336…4，
∴这一列数中的第2020个数是7．
故答案为：C．
【例4－1】（2020·南京市溧水区月考）比较大小： ________0.5．（填“＞”“＜”或“＝”）
【答案】＜.
【解析】解：∵1<3＜4，
∴1<＜2，
∴0<－1＜1
∴0<＜0.5
故答案为：＜．
【变式4－1】（2021·四川遂宁月考）已知8＋＝x＋y，其中x是一个整数，0 【答案】19.
【解析】解：∵
∴，即
∵x是一个整数，0 ∴x=9，y=
∴2x＋(y－)2=
故答案为：19．
知识点三：实数与数轴
【例5－1】（2020·浙江开化县期中）如图1是由8个同样大小的立方体组成的魔方，体积为64，图中阴影部分是一个正方形ABCD，现把正方形ABCD放到数轴上（如图2），使得A与重合，那么D在数轴上表示的数为（ ）

A． B． C． D．
【答案】C.
【解析】解：∵=4，
∴这个魔方的棱长为4，
∴小正方体的棱长为2，
∴阴影部分的面积为：8，
∴小正方体的边长为：，
∴点D在数轴上表示的数为，
故答案为：C．
【变式5－1】（2020·上海月考）如图，线段AB将边长为1个单位长度的正方形分割为两个等腰直角三角形，以A为圆心，AB的长度为半径画弧交数轴于点C，那么点C在数轴上表示的实数是（ ）

A． B． C． D．1
【答案】A.
【解析】解：AB=，C点表示的数是：+1，
故答案为：A．
【变式5－2】（2020·河北邢台期中）如图，直径为1个单位长度的圆从A点沿数轴向右滚动（无滑动）两周到达点B，则点B表示的数是（ ）

A． B． C． D．
【答案】B.
【解析】解：由题意得：圆的周长为π，
所以，B点表示的数为2π－1.
故答案为：B．
知识点四：新定义下的实数概念
【例6－1】规定用符号表示一个实数的整数部分，例如，，则（　　　）
A．5 B．4 C．3 D．2
【答案】B.
【解析】解：∵
∴
∴的整数部分为4
∴4
故答案为：B．
【例6－2】（2020·浙江衢州期中）已知 表示取三个数中最小的那个数，例如：当x=9时， ．当 时，则x的值为（   ）
A．                            B．                         C．                                       D．
【答案】A.
【解析】解：当=时，x=<，故不符题意；
当x2=时，x=或x=－（不符合题意），此时=>，符合题意
当x=时，=，x2= 综上所述，x=
故答案为：A．
【变式6－1】（2020·宁波期中）设表示大于x的最小整数，如，，则下列结论中正确的有（ ）
①；
②的最小值是0；
③存在实数x，使成立
A．1个 B．2个 C．3个 D．0个
【答案】A.
【解析】解：①=1，故①错误；
②，故②错误；
③存在实数x=0.5，使成立，故④正确
故答案为：A.
【变式6－2】（2020·浙江期末）任何一个正整数n都可以进行这样的分解：n＝s×t（s，t是正整数，且s≤t），如果p×q在n的所有分解中两因数之差的绝对值最小，我们就称p×q是n的最优分解，并规定：F（n）＝．例如24可以分解成1×24，2×12，3×8，4×6这四种，这时就有F（24）＝＝．给出下列关于F（n）的说法：①F（6）＝；②F（16）＝1；③若n是一个自然数的平方，F（n）＝1．其中说法正确的个数是（ ）
A．1 B．2 C．3 D．0
【答案】C.
【解析】解：①∵6＝1×6＝2×3，
∴F（6）＝，正确；
②∵16＝1×16＝2×8＝4×4，
∴F（16）＝＝1，正确；
③∵n是一个自然数的平方，
∴n分解成两个完全相同的数时，差的绝对值最小，
∴F（n）＝1，正确．
综上所述，说法正确的个数是3，
故答案为：C．
知识点五：实数综合题型
【例7－1】（2020·山东滨州期末）大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部写出来，于是可以用表示的小数部分，因为的整数部分是，将这个数减去其整数部分，差就是小数部分．已知，其中是整数，且那么 ______．
【答案】6－.
【解析】解：∵2<<3,0 ∴4<+2<5，
∴a=4，b=－2
a－b=4－（－2）=6－.
故答案为：6－.
【例7－2】（2020·浙江台州期末）公元3世纪，我国数学家刘徽就能利用近似公式得到根式的近似值.利用此公式就可以估计的近似值，______（精确到0.01）．
【答案】3.17.
【解析】解：根据题意得：，
∴=3+0.17=3.17.
故答案为：3.17．
【例7－3】阅读理解
把几个数用大括号围起来，中间用逗号断开，如：{3，4}，{﹣3，6，8，18}，我们称之为集合，其中大括号内的数称其为集合的元素．如果一个集合满足：只要其中有一个元素a，使得﹣2a+4也是这个集合的元素，这样的集合我们称为条件集合，例如：集合{3，﹣2}，因为﹣2×3+4＝﹣2，﹣2恰好是这个集合的元素，所以{3，﹣2}是条件集合；例如：集合{﹣2，9，8}，因为﹣2×（﹣2）+4＝8，8恰好是这个集合的元素，所以{﹣2，9，8}是条件集合．
（1）集合{﹣4，12} 条件集合；集合{，，} 条件集合（填“是”或“不是”）
（2）若集合{8，10，n}和集合{﹣m}都是条件集合，求m，n的和．
【答案】（1）是，是；（2）m，n的和为：﹣13，﹣17，﹣3，﹣4，0
【解析】解：（1）∵﹣4×（﹣2）+4＝12，
∴集合{﹣4，12}是条件集合；
∵（﹣2）+4，
∴集合{，，}是条件集合；
故答案为：是，是；
（2）∵集合{8，10，n}和集合{﹣m}都是条件集合，
∴若n＝﹣2×8+4，则n＝﹣12；
若n＝﹣2×10+4，则n＝﹣16；
若﹣2n+4＝8，则n＝﹣2；
若﹣2n+4＝10，则n＝﹣3；
若﹣2n+4＝n，则n；
若﹣m×（﹣2）+4＝﹣m，则m；
∴m，n的和为：﹣13，﹣17，﹣3，﹣4，0．
【变式7－1】（2020·北京海淀区考试）阅读下面求（m0）近似值的方法，回答问题：
①任取正数a1；
②令a2＝（a1+），则；
③a3＝（a2+），则；
…以此类推n次，得到．
其中an，称为的n阶过剩近似值，称为的n阶不足近似值．
仿照上述方法，求的近似值．
①取正数a1＝3．
②于是a2＝_____；则_____＜＜a2．
③的3阶不足近似值是_____．
【答案】；；.
【解析】解：
∴
∴
∴
故答案为：② ③
【变式7－2】（2020·浙江衢州期中）教材中的探究：如图，把两个边长为1的小正方形沿对角线剪开，用所得到的4个直角三角形拼成一个面积为2的大正方形．由此，得到了一种能在数轴上画出无理数对应点的方法（数轴的单位长度为1）．

图1 图2
（1）阅读理解：图1中大正方形的边长为________，图2中点A表示的数为________；
（2）迁移应用：
请你参照上面的方法，把5个小正方形按图3位置摆放，并将其进行裁剪，拼成一个大正方形．
①请在图3中画出裁剪线，并在图3中画出所拼得的大正方形的示意图．
②利用①中的成果，在图4的数轴上分别标出表示数－0.5以及 的点，并比较它们的大小．

图3 图4
【答案】（1）；（2）见解析.
【解析】解：设正方形边长为a，
∵a2=2，
∴a=，
故答案为：，；
（2）解：①裁剪后拼得的大正方形如图所示：

②设拼成的大正方形的边长为b，
∴b2=5，
∴b=±，
在数轴上以－3为圆心，以大正方形的边长为半径画弧交数轴的右方与一点M，则M表示的数为－3+，可知，表示－0.5的N点在M点的右方，

∴．
【变式7－3】（2020·江苏泰州姜堰区月考）因为的整数部分是1，将这个数减去其整数部分，差就是小数部分.例如: ，即 的整数部分2，小数部分为 .
(1)如果的小数部分为a， 的整数部分为b，求的值；
(2)已知: 其中x是整数，且0＜y＜1，求x－y的相反数.
【答案】(1)1； (2).
【解析】解：(1) ∵，
∴整数数部分为2，小数部分为a=
∵，
∴整数数部分为，b=3
∴
（2）由题意得
∵x是整数，0＜y＜1
∴
∴的相反数为.
【变式7－4】（2020·沙坪坝区月考）我们把能被13整除的数称为“自觉数”，已知一个整数，把其个位数字去掉，再从余下的数中，加上个位数的4倍，如果和是13的倍数，则原数为“自觉数”．如果数字仍然太大不能直接观察出来，就重复此过程．如，所以416是“自觉数”；又如，因为30不能被13整除，所以25281不是“自觉数”．
判断27365是否为“自觉数”（填“是”或者“否”），并证明任意一个三位数，若能被13整除，则三位数是“自觉数”.
【答案】见解析.
【解析】解：（1）2736+4×5=2756，
275+4×6=299，
29+4×9=65，
65能被13整除，
∴27365是自觉数；
令+4c=13m（m为整数），
即10a+b+4c=13m，
∴10a+b=13m－4c
∴三位数=100a+10b+c
=10（10a+b）+c
=10（13m－4c）+c
=130m－40c+c
=130m－39c
（130m－39c）÷13=10m－3c
∵m，c为整数
∴任意一个三位数，若能被13整除，则三位数是“自觉数”.