数学4.2 平行四边形课堂教学ppt课件

这是一份数学4.2 平行四边形课堂教学ppt课件，共17页。PPT课件主要包含了新知导入，情境引入，折一折，合作探究，新知讲解，提炼概念，典例精讲，勾股定理，课堂练习，课堂总结等内容，欢迎下载使用。

为迎接“五一旅游黄金周”的到来，某风景区正在精心“装扮”，静待佳客来临。打算在风景区的入口处建一个形状如图所示的花坛。
现在想在花坛里种上四种不同颜色的花并且这四种花正好将花坛分成面积相等的四块，你能帮忙划分吗？把你的划分方案向大家展示一下好吗？
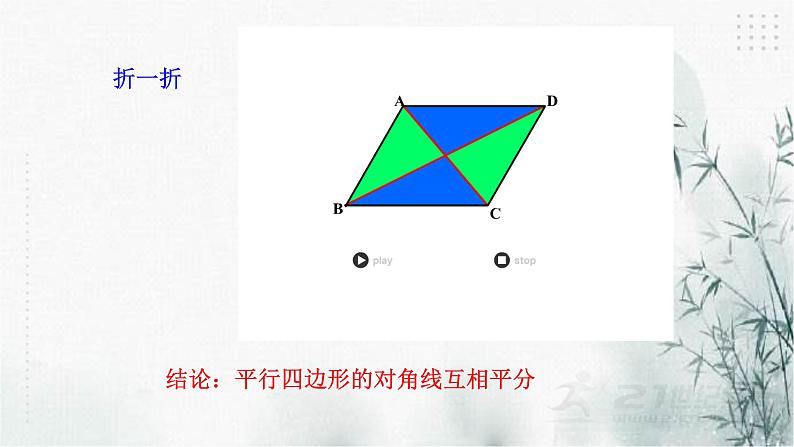
想一想：平行四边形的对角线有什么关系？
结论：平行四边形的对角线互相平分
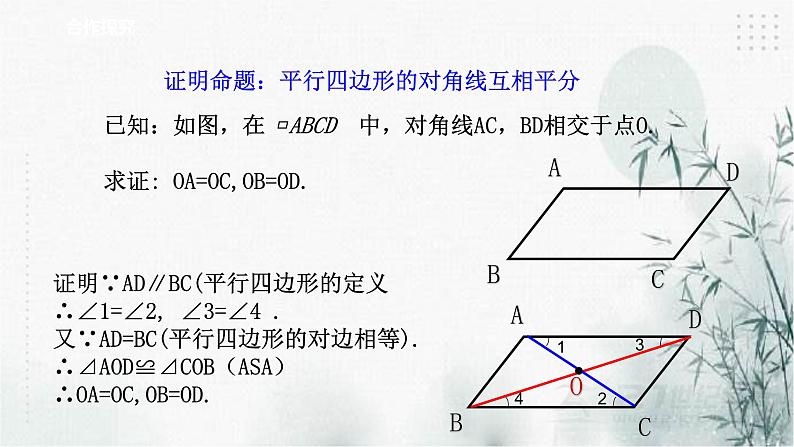
证明命题：平行四边形的对角线互相平分
已知：如图，在 ▱ABCD 中，对角线AC，BD相交于点O.求证: OA=OC,OB=OD.
证明∵AD∥BC(平行四边形的定义∴∠1=∠2, ∠3=∠4 .又∵AD=BC(平行四边形的对边相等).∴⊿AOD≌⊿COB（ASA）∴OA=OC,OB=OD.
几何语言：∵ 四边形ABCD是平行四边形∴ OA＝OC，OB＝OD．（平行四边形的对角线互相平分）或在▱ABCD中，OA＝OC，OB＝OD．（平行四边形的对角线互相平分）或AC=2AO=2CO，BD=2BO=2DO
性质：平行四边形的对角线互相平分
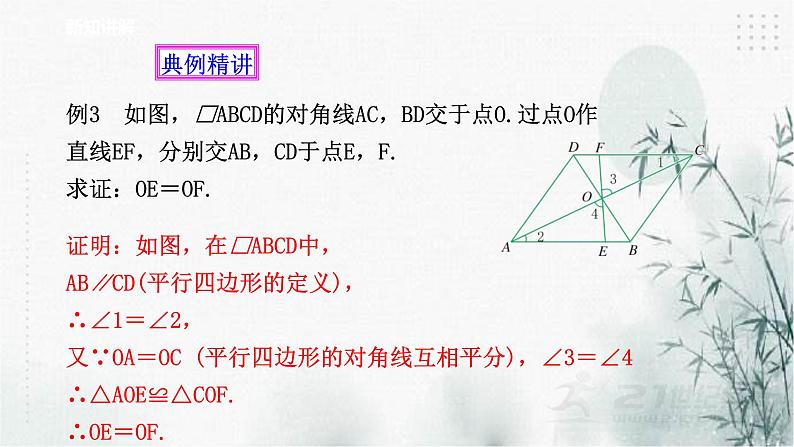
例3 如图，□ABCD的对角线AC，BD交于点O.过点O作直线EF，分别交AB，CD于点E，F.求证：OE＝OF.
证明：如图，在□ABCD中，AB∥CD(平行四边形的定义)，∴∠1＝∠2，又∵OA＝OC (平行四边形的对角线互相平分)，∠3＝∠4∴△AOE≌△COF.∴OE＝OF.
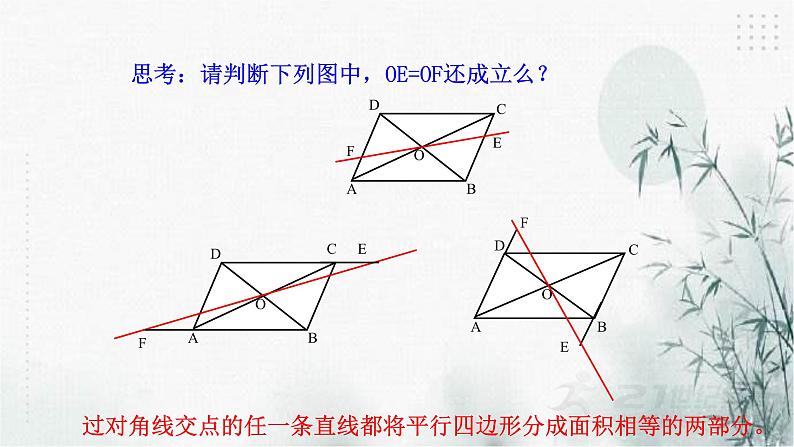
思考：请判断下列图中，OE=OF还成立么？
过对角线交点的任一条直线都将平行四边形分成面积相等的两部分。
想一想有一块平行四边形的草地，学校想在中间留一条小路，把它分成面积相等的两块，请你来想想，可以怎样分？有多少种分法？
有无数种分法，分割线只要过对角线的交点
例4 如图，在□ABCD中，对角线AC，BD交于点E，AC⊥BC.若AC＝4，AB＝5，求BD的长.
∴BD=2BE=
解：∵ AC⊥BC∴BC2=AB2-AC2=25=16=9（勾股定理）∴ BC=3∵ 四边形ABCD是平行四边形∴CE=AC=2，BD=2BE（平行四边形对角线互相平分）
1.已知▱ABCD的对角线AC，BD相交于点O，AC＝6，BD＝8，AB的长为5，则△AOB的周长为________．
【解析】 ∵▱ABCD的对角线AC，BD相交于点O，AC＝6，BD＝8，∴AO＝3，BO＝4.AB=5，∴△AOB的周长12。
2.四边形ABCD是平行四边形，AB＝10，AD＝8，AC⊥BC，求BC，CD，AC，OA的长以及▱ABCD的面积．
解：∵四边形ABCD是平行四边形，∴BC＝AD＝8，CD＝AB＝10，∵AC⊥BC，∴AC＝＝＝6，∴OA＝3，S▱ABCD＝BC·AC＝8×6＝48.
3.已知▱ABCD和▱EBFD的顶点A，E，F，C在一条直线上． 求证：AE＝CF.
证明：如答图，连结BD，交AC于点O.∵四边形ABCD和四边形EBFD是平行四边形，∴AO＝CO，EO＝FO，∴AO－EO＝CO－FO，即AE＝CF.
【点悟】由于学习了全等三角形，思维还停留在三角形范围内，有时一看是证明两线段相等且又属于两个不同的三角形，就想证这两个三角形全等，却忽视了平行四边形特有的性质，因此在证明平行四边形的有关问题时，应注意尽量运用平行四边形的性质．
1.平行四边形的一些问题往往要转化为三角形的问题，所以要注意把平行四边形的知识与三角形的相关知识结合起来应用．2.根据平行四边形的对边相等，对角线互相平分及勾股定理，平行四边形的面积公式进行推理与计算．3.对角线间的关系是平行四边形中很重要的关系，解涉及到线段平分的问题时，通常可通过此性质求解．