



还剩7页未读,
继续阅读
人教B版 (2019)必修 第二册5.3.5 随机事件的独立性课文课件ppt
展开
这是一份人教B版 (2019)必修 第二册5.3.5 随机事件的独立性课文课件ppt,共13页。
1.定义一般地,当P(AB)=① P(A)P(B) 时,就称事件A与B相互独立(简称独立).事件A与 B相互独立的直观理解是,事件A是否发生不会影响事件B发生的概率,事件B是否 发生也不会影响事件A发生的概率.
2.性质(1)如果事件A与B相互独立,则 与B,A与 , 与 也相互独立.(2)若事件A与B相互独立,则P(A∩B)=② P(A)×P(B) ,即两个相互独立事件同时 发生的概率等于每个事件发生的概率的③ 积 .(3)如果事件A1,A2,…,An相互独立,那么这n个事件都发生的概率等于每个事件发生 的概率的积,即P(A1∩A2∩…∩An)=P(A1)×P(A2)×…×P(An).并且上式中任意多个事 件Ai换成其对立事件 后等式仍成立.
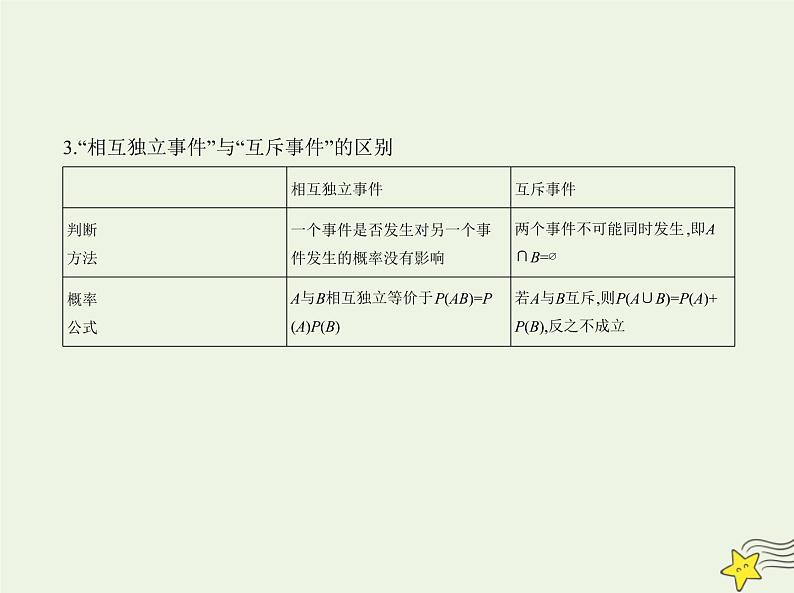
3.“相互独立事件”与“互斥事件”的区别
判断正误,正确的画“ √” ,错误的画“ ✕” 。
1.若任意两个事件A,B互斥,则P(A∩B)=P(A)×P(B). ( ✕ )
2.若事件A与B相互独立,A与 相互独立,则B与 也相互独立. ( ✕ )
3.两事件相互独立,则两事件一定互斥. ( ✕ )
4.若A,B相互独立,且P(A)=0.5,P(B)=0.4,则A,B都不发生的概率为0.3. ( √ )
1 |相互独立事件发生的概率
判断两个事件是否相互独立的方法
1.直接法:直接判断一个事件发生与否是否影响另一事件发生的概率.
2.定义法:判断P(AB)=P(A)P(B)是否成立.
3.转化法:由判断事件A与事件B是否相互独立,转化为判断A与 , 与B, 与 是否具有独立性.
若事件A与B相互独立,则P(AB)=P(A)P(B),则:(1)P(A )=P(A)-P(AB)=P(A)-P(A)P(B)=P(A)·[1-P(B)]=P(A)P( );(2)P( B)=P(B)-P(AB)=P(B)-P(A)P(B)=[1-P(A)]P(B)=P( )P(B);(3)P( )=P( )-P( B)=P( )-P( )P(B)=P( )·[1-P(B)]=P( )P( ).
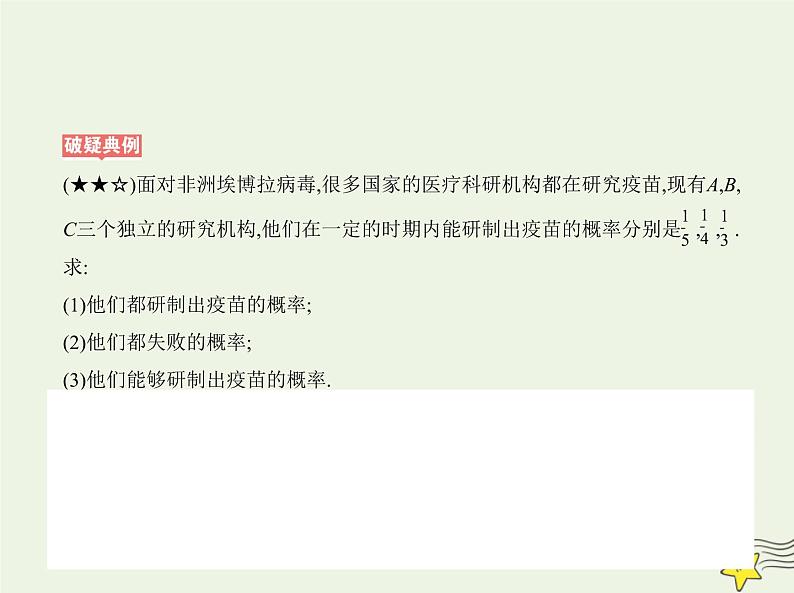
(★★☆)面对非洲埃博拉病毒,很多国家的医疗科研机构都在研究疫苗,现有A,B, C三个独立的研究机构,他们在一定的时期内能研制出疫苗的概率分别是 , , .求:(1)他们都研制出疫苗的概率;(2)他们都失败的概率;(3)他们能够研制出疫苗的概率.
解析 令事件A,B,C分别表示A,B,C三个独立的研究机构在一定时期内成功研制 出该疫苗,依题意可知,事件A,B,C相互独立,且P(A)= ,P(B)= ,P(C)= .(1)若他们都研制出疫苗,即事件A,B,C同时发生,故P(A∩B∩C)=P(A)×P(B)×P(C)= × × = .
(2)若他们都失败,即事件 , , 同时发生,故P( ∩ ∩ )=P( )×P( )×P( )=[1-P(A)][1-P(B)][1-P(C)]= × × = × × = .(3)“他们能够研制出疫苗”的对立事件为“他们都失败”,结合对立事件间的 概率关系可得所求事件的概率P=1-P( ∩ ∩ )=1- = .
方法总结 求相互独立事件同时发生的概率的步骤:(1)确定各事件之间是相互独立的;(2)确定这些事件可以同时发生;(3)求出每个事 件发生的概率,再求其积.
2|相互独立事件的实际应用
在一次三人象棋对抗赛中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率 为0.6,比赛顺序如下:第一局,甲对乙;第二局,第一局胜者对丙;第三局,第二局胜者 对第一局败者;第四局,第三局胜者对第二局败者.
1.如果乙要连胜四局,比赛应如何进行?提示:若要乙连胜四局,则对阵情况是第一局:甲对乙,乙胜;第二局:乙对丙,乙胜;第 三局:乙对甲,乙胜;第四局:乙对丙,乙胜.
2.要求出乙连胜四局时的概率需要用到哪些概率知识?如何求?提示:应用事件的独立性知识,按照每局乙胜的情况分析,所求概率为P=(1-0.4)2×0. 52=0.32=0.09.
求复杂事件的概率一般可分三步进行:(1)列出题中涉及的各个事件,并用适当的符号表示它们;(2)理清各事件之间的关系,用事件间的“并”“交”恰当地表示所求事件;(3)根据事件之间的关系准确地运用概率公式进行计算.注意:当直接计算符合条件的事件的概率较复杂时,可先间接地计算其对立事件 的概率,再求出符合条件的事件的概率.
(★★★)红队队员甲、乙、丙与蓝队队员A,B,C进行围棋比赛,甲对A、乙对B、 丙对C各一盘.已知甲胜A、乙胜B、丙胜C的概率分别为0.6,0.5,0.5.假设各盘比赛 结果相互独立.求:(1)红队中有且只有一名队员获胜的概率;(2)红队中至少有两名队员获胜的概率.思路点拨:弄清事件“红队中有且只有一名队员获胜”与事件“红队中至少有两名队员获 胜”是由哪些基本事件组成以及这些事件间的关系,然后选择相应概率公式求 解.
解析 设甲胜A为事件D,乙胜B为事件E,丙胜C为事件F,则 , , 分别表示A胜甲、B胜乙、C胜丙.因为P(D)=0.6,P(E)=0.5,P(F)=0.5,所以由对立事件的概率公式知P( )=0.4,P( )=0.5,P( )=0.5.(1)红队中有且只有一名队员获胜的事件有D∩ ∩ , ∩E∩ , ∩ ∩F,以上3个事件彼此互斥且相互独立.所以红队中有且只有一名队员获胜的概率P1=P[(D∩ ∩ )∪( ∩E∩ )∪( ∩ ∩F)]=P(D∩ ∩ )+P( ∩E∩ )+P( ∩ ∩F)=0.6×0.5×0.5+0.4×0.5×0.5+0.4×0.5×0.5=0.35.(2)解法一:红队中至少有两名队员获胜的事件有D∩E∩F,D∩E∩ ,D∩ ∩F, ∩E∩F,由于以上四个事件两两互斥且各盘比赛的结果相互独立,因此红队中至少有两名队员获胜的概率P2=P(D∩E∩F)+P(D∩E∩ )+P(D∩
1.定义一般地,当P(AB)=① P(A)P(B) 时,就称事件A与B相互独立(简称独立).事件A与 B相互独立的直观理解是,事件A是否发生不会影响事件B发生的概率,事件B是否 发生也不会影响事件A发生的概率.
2.性质(1)如果事件A与B相互独立,则 与B,A与 , 与 也相互独立.(2)若事件A与B相互独立,则P(A∩B)=② P(A)×P(B) ,即两个相互独立事件同时 发生的概率等于每个事件发生的概率的③ 积 .(3)如果事件A1,A2,…,An相互独立,那么这n个事件都发生的概率等于每个事件发生 的概率的积,即P(A1∩A2∩…∩An)=P(A1)×P(A2)×…×P(An).并且上式中任意多个事 件Ai换成其对立事件 后等式仍成立.
3.“相互独立事件”与“互斥事件”的区别
判断正误,正确的画“ √” ,错误的画“ ✕” 。
1.若任意两个事件A,B互斥,则P(A∩B)=P(A)×P(B). ( ✕ )
2.若事件A与B相互独立,A与 相互独立,则B与 也相互独立. ( ✕ )
3.两事件相互独立,则两事件一定互斥. ( ✕ )
4.若A,B相互独立,且P(A)=0.5,P(B)=0.4,则A,B都不发生的概率为0.3. ( √ )
1 |相互独立事件发生的概率
判断两个事件是否相互独立的方法
1.直接法:直接判断一个事件发生与否是否影响另一事件发生的概率.
2.定义法:判断P(AB)=P(A)P(B)是否成立.
3.转化法:由判断事件A与事件B是否相互独立,转化为判断A与 , 与B, 与 是否具有独立性.
若事件A与B相互独立,则P(AB)=P(A)P(B),则:(1)P(A )=P(A)-P(AB)=P(A)-P(A)P(B)=P(A)·[1-P(B)]=P(A)P( );(2)P( B)=P(B)-P(AB)=P(B)-P(A)P(B)=[1-P(A)]P(B)=P( )P(B);(3)P( )=P( )-P( B)=P( )-P( )P(B)=P( )·[1-P(B)]=P( )P( ).
(★★☆)面对非洲埃博拉病毒,很多国家的医疗科研机构都在研究疫苗,现有A,B, C三个独立的研究机构,他们在一定的时期内能研制出疫苗的概率分别是 , , .求:(1)他们都研制出疫苗的概率;(2)他们都失败的概率;(3)他们能够研制出疫苗的概率.
解析 令事件A,B,C分别表示A,B,C三个独立的研究机构在一定时期内成功研制 出该疫苗,依题意可知,事件A,B,C相互独立,且P(A)= ,P(B)= ,P(C)= .(1)若他们都研制出疫苗,即事件A,B,C同时发生,故P(A∩B∩C)=P(A)×P(B)×P(C)= × × = .
(2)若他们都失败,即事件 , , 同时发生,故P( ∩ ∩ )=P( )×P( )×P( )=[1-P(A)][1-P(B)][1-P(C)]= × × = × × = .(3)“他们能够研制出疫苗”的对立事件为“他们都失败”,结合对立事件间的 概率关系可得所求事件的概率P=1-P( ∩ ∩ )=1- = .
方法总结 求相互独立事件同时发生的概率的步骤:(1)确定各事件之间是相互独立的;(2)确定这些事件可以同时发生;(3)求出每个事 件发生的概率,再求其积.
2|相互独立事件的实际应用
在一次三人象棋对抗赛中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率 为0.6,比赛顺序如下:第一局,甲对乙;第二局,第一局胜者对丙;第三局,第二局胜者 对第一局败者;第四局,第三局胜者对第二局败者.
1.如果乙要连胜四局,比赛应如何进行?提示:若要乙连胜四局,则对阵情况是第一局:甲对乙,乙胜;第二局:乙对丙,乙胜;第 三局:乙对甲,乙胜;第四局:乙对丙,乙胜.
2.要求出乙连胜四局时的概率需要用到哪些概率知识?如何求?提示:应用事件的独立性知识,按照每局乙胜的情况分析,所求概率为P=(1-0.4)2×0. 52=0.32=0.09.
求复杂事件的概率一般可分三步进行:(1)列出题中涉及的各个事件,并用适当的符号表示它们;(2)理清各事件之间的关系,用事件间的“并”“交”恰当地表示所求事件;(3)根据事件之间的关系准确地运用概率公式进行计算.注意:当直接计算符合条件的事件的概率较复杂时,可先间接地计算其对立事件 的概率,再求出符合条件的事件的概率.
(★★★)红队队员甲、乙、丙与蓝队队员A,B,C进行围棋比赛,甲对A、乙对B、 丙对C各一盘.已知甲胜A、乙胜B、丙胜C的概率分别为0.6,0.5,0.5.假设各盘比赛 结果相互独立.求:(1)红队中有且只有一名队员获胜的概率;(2)红队中至少有两名队员获胜的概率.思路点拨:弄清事件“红队中有且只有一名队员获胜”与事件“红队中至少有两名队员获 胜”是由哪些基本事件组成以及这些事件间的关系,然后选择相应概率公式求 解.
解析 设甲胜A为事件D,乙胜B为事件E,丙胜C为事件F,则 , , 分别表示A胜甲、B胜乙、C胜丙.因为P(D)=0.6,P(E)=0.5,P(F)=0.5,所以由对立事件的概率公式知P( )=0.4,P( )=0.5,P( )=0.5.(1)红队中有且只有一名队员获胜的事件有D∩ ∩ , ∩E∩ , ∩ ∩F,以上3个事件彼此互斥且相互独立.所以红队中有且只有一名队员获胜的概率P1=P[(D∩ ∩ )∪( ∩E∩ )∪( ∩ ∩F)]=P(D∩ ∩ )+P( ∩E∩ )+P( ∩ ∩F)=0.6×0.5×0.5+0.4×0.5×0.5+0.4×0.5×0.5=0.35.(2)解法一:红队中至少有两名队员获胜的事件有D∩E∩F,D∩E∩ ,D∩ ∩F, ∩E∩F,由于以上四个事件两两互斥且各盘比赛的结果相互独立,因此红队中至少有两名队员获胜的概率P2=P(D∩E∩F)+P(D∩E∩ )+P(D∩













