

所属成套资源:北师大版2022年数学中考一轮复习考点透析
考点23全等三角形(解析版)-2022年数学中考一轮复习考点透析(北师大版)
展开
这是一份考点23全等三角形(解析版)-2022年数学中考一轮复习考点透析(北师大版),共31页。
考点23全等三角形
【命题趋势】
全等三角形的性质与判定,主要以选择题、填空题、解答题的形式来考查。考查内容有:①判断全等三角形的对应边;②证明两个三角形全等;③判断全等三角形的对数;④补充条件使两个三角形全等;⑤通过证明两个三角形全等得到线段相等,一般命基础题和中档题。
【常考知识】
全等三角形的性质与判定。主要有:①判断全等三角形的对应边;②证明两个三角形全等;③判断全等三角形的对数;④补充条件使两个三角形全等;⑤通过证明两个三角形全等得到线段相等
【夺分技巧】
①“HL”只适合直角三角形全等的判定。
②“ SSA” 和“AAA” 不能判定两个三角形全等。判定两个三角形全等时,必须有边的参与。
③证明两个三角形全等时,对应字母的顶点须写在对应的位置上,养成良好的书写习惯。
真题演练
一、单选题
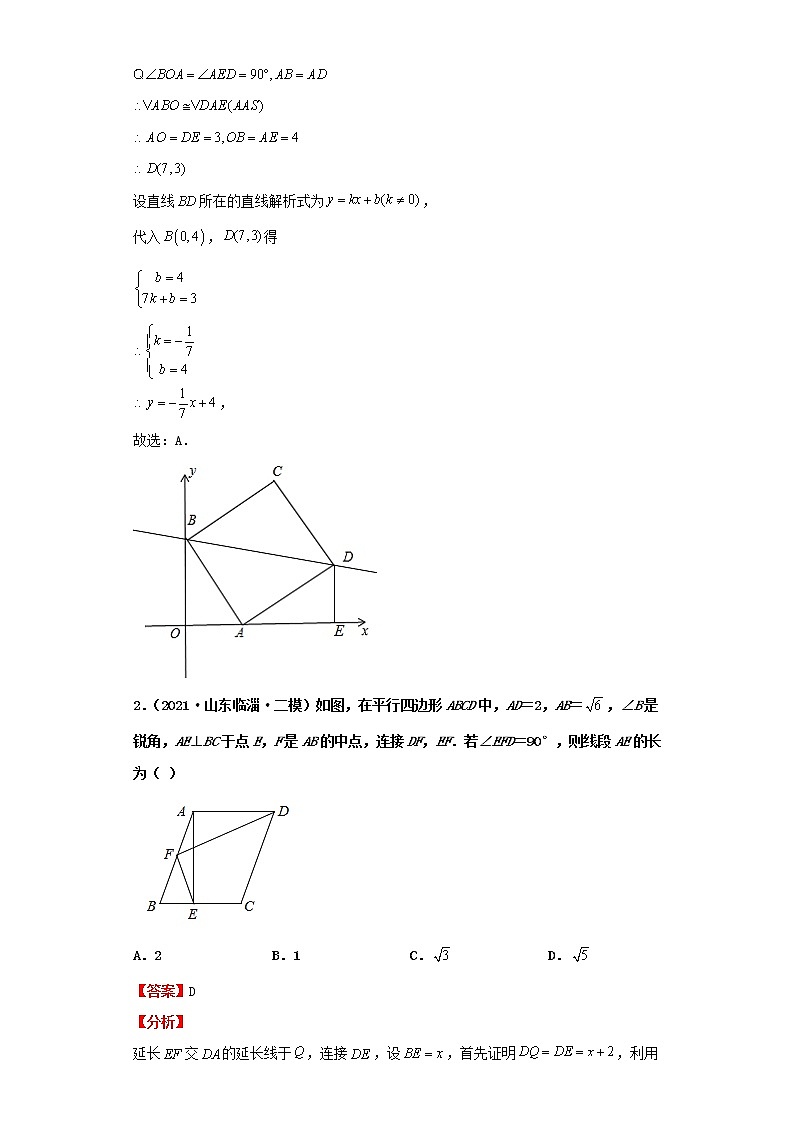
1.(2021·内蒙古呼和浩特·中考真题)在平面直角坐标系中,点,.以为一边在第一象限作正方形,则对角线所在直线的解析式为( )
A. B. C. D.
【答案】A
【分析】
过点作轴于点,先证明,再由全等三角形对应边相等的性质解得,最后由待定系数法求解即可.
【详解】
解:正方形中,过点作轴于点,
设直线所在的直线解析式为,
代入,得
,
故选:A.
2.(2021·山东临淄·二模)如图,在平行四边形ABCD中,AD=2,AB=,∠B是锐角,AE⊥BC于点E,F是AB的中点,连接DF,EF.若∠EFD=90°,则线段AE的长为( )
A.2 B.1 C. D.
【答案】D
【分析】
延长交的延长线于,连接,设,首先证明,利用勾股定理构建方程即可求解.
【详解】
解:如图,延长交的延长线于,连接,设,
四边形是平行四边形,
,
,
,
,
,
,
,
,
,
,
,
解得:(舍去)
,
,
故选:D.
3.(2021·云南五华·二模)如图,方格纸中每个小正方形的边长均为1,其顶点称为格点.的顶点都在小正方形的格点上.以点为圆心,适当长为半径画弧,交于点 ,交于点;分别以点,为圆心,大于的长为半径画弧,两弧在 的内部相交于点;画射线交于点,设.点 为线段上的动点,则下列结论:①;②若分别连接 ,,则;③当时, ;④的最小值为.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】D
【分析】
根据方格纸中每个小正方形的边长均为1, 的顶点都在小正方形的格点上,可求得,,,根据勾股定理可得到是直角三角形,可判断①;根据角平分线的作法,可判断②;根据相似三角形的判定可判断③;根据角平分线的性质可判断④;综合判断后,可得到结果.
【详解】
解:∵方格纸中每个小正方形的边长均为1, 的顶点都在小正方形的格点上,
∴,, ,
∴
即是直角三角形,
∴,故①正确;
∵以点,为圆心,大于的长为半径画弧,两弧在的内部相交于点 ,
∴由以上作法可知,是的角平分线,且,故②正确;
当时,
∵
∴
∴,故③正确;
∵点为线段上的动点,当时,最小,
又∵是的角平分线,,
∴,故④正确,
综上所述,正确的是①②③④,
故选:D.
4.(2021·浙江温州·中考真题)由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.过点作的垂线交小正方形对角线的延长线于点,连结,延长交于点.若,则的值为( )
A. B. C. D.
【答案】C
【分析】
如图,设BH交CF于P,CG交DF于Q,根据题意可知BE=PC=DF,AE=BP=CF,根据可得BE=PE=PC=PF=DF,根据正方形的性质可证明△FDG是等腰直角三角形,可得DG=FD,根据三角形中位线的性质可得PH=FQ,CH=QH=CQ,利用ASA可证明△CPH≌△GDQ,可得PH=QD,即可得出PH=BE,可得BH=,利用勾股定理可用BE表示长CH的长,即可表示出CG的长,进而可得答案.
【详解】
如图,设BH交CF于P,CG交DF于Q,
∵由四个全等的直角三角形和一个小正方形组成的大正方形,
∴BE=PC=DF,AE=BP=CF,
∵,
∴BE=PE=PC=PF=DF,
∵∠CFD=∠BPC,
∴DF//EH,
∴PH为△CFQ的中位线,
∴PH=QF,CH=HQ,
∵四边形EPFN是正方形,
∴∠EFN=45°,
∵GD⊥DF,
∴△FDG是等腰直角三角形,
∴DG=FD=PC,
∵∠GDQ=∠CPH=90°,
∴DG//CF,
∴∠DGQ=∠PCH,
在△DGQ和△PCH中,,
∴△DGQ≌△PCH,
∴PH=DQ,CH=GQ,
∴PH=DF=BE,CG=3CH,
∴BH=BE+PE+PH=,
在Rt△PCH中,CH==,
∴CG=BE,
∴.
故选:C.
5.(2021·浙江·温州市教育教学研究院一模)《几何原本》关于毕达哥拉斯定理,欧几里德给出证明.如图,中,,以AC,BC,AB为边分别向外作正方形,连结CD,CE,过C作,的面积为,的面积为,若,,则正方形BCGH的边长( )
A. B. C. D.
【答案】C
【分析】
过D作DM⊥AC,过E作EN⊥BC,设CF交AB于J,证明≌,≌,分别得到,,分别得到和,根据,可得,设,可求出CJ和FJ,根据CF=13求出x值,从而可得BC.
【详解】
解:过D作DM⊥AC,延长CA交DM于点M,过E作EN⊥BC,设CF交AB于J,
∵,
∴,
又∵,
∴,
∴在与中,
,
∴≌,
∴,
同理,≌,
∴,
,,
∵,
∴,即,
设,则,,
∴,,,
∴,,
∴,
∴,
∴正方形BCGH边长.
故选C.
6.(2021·河南·一模)如图,在平面直角坐标系中,点A,B的坐标分别为,,连接,分别以点A,点B为圆心,长为半径画弧,两弧在第一象限交于点C.则点C的坐标为( )
A. B. C. D.
【答案】D
【分析】
如图,连接 作射线 交于 过作于过作于 再求解 证明是的垂直平分线,再求解再利用相似三角形的性质可得答案.
【详解】
解:如图,连接 作射线 交于 过作于过作于
点A,B的坐标分别为,,
是的垂直平分线,
同理可得:
故选:
7.(2021·陕西·西安铁一中滨河学校三模)在中,,cm,的平分线交于D,且,则点D到的距离等于( )
A.cm B.cm C.cm D.cm
【答案】A
【分析】
根据比例求出的长,再过点D作于E.根据角平分线上的点到角的两边的距离相等可得,即可得解.
【详解】
解:,,CD+BD=BC=16,
,
过点D作于E,
是的平分线,,
,
即点D到的距离是.
故选:A.
8.(2021·山西太原·二模)如图,在矩形纸片中,,,点是上一点,点在上,将矩形纸片沿直线折叠,点落在点处.点恰好落在边上的点处,交于点,若,则四边形的面积等于( )
A. B. C. D.
【答案】D
【分析】
根据矩形的性质得,设,由勾股定理得,再证明得,由勾股定理得,可得,设由勾股定理求出,最后由四边形的面积求出结论即可.
【详解】
解:∵四边形ABCD是矩形,且
∴
∵
∴
设
∴
∵且
∴
∴
∴
∵∠
∴∠,
∴
∵
∴
∴
∴
∵
∴
设
∴
又
∴
解得,
∴
∵,
∴四边形的面积
故选:D
9.(2021·江苏·南京市第十二初级中学八年级期中)如图,,再添加一个条件,不能判定的是( )
A. B. C. D.
【答案】B
【分析】
根据全等三角形的判定条件进行逐一判断即可得到答案.
【详解】
解:由题意得:∠CAB=∠DBA,AB=BA,
当AC=BD时,可以利用SAS证明△ABC≌△BAD,故A选项不符合题意;
当AD=BC时,可以利用SSA不能证明△ABC≌△BAD,故B选项符合题意;
当∠DAB=∠CBA时,可以利用ASA证明△ABC≌△BAD,故C选项不符合题意;
当∠C=∠D时,可以利用AAS证明△ABC≌△BAD,故D选项不符合题意;
故选B.
10.(2021·山东·滨州实验学校八年级期中)工人常用角尺平分一个任意角,做法如下:如图,是一个任意角,在边、上分别取,移动角尺,使角尺两边相同的刻度分别与点、重合,过角尺顶点作射线,由此作法便可得,共依据是( )
A. B. C. D.
【答案】A
【分析】
由作图过程可得MO=NO,NC=MC,再加上公共边CO=CO可利用SSS定理判定△MOC≌△NOC.
【详解】
解:由作图过程可得MO=NO,NC=MC,
在△ONC和△OMC中,
∴△MOC≌△NOC(SSS),
∴∠BOC=∠AOC,
故选:A.
二、填空题
11.(2021·广东·深圳市南山外国语学校二模)如图,在平面直角坐标系中,矩形中,,,将沿对角线翻折,使点落在处,与轴交于点,则点的坐标为______.
【答案】
【分析】
设,则,由题意可以求证,从而得到,再根据勾股定理即可求解.
【详解】
解:由题意可知:,,
设,则,
又∵
∴
∴
在中,,即
解得:
∴点的坐标为
故答案为
12.(2021·江苏秦淮·二模)如图,在中,.将绕点C顺时针旋转后得,且点落在边上,连接.若,则四边形的面积为_________.
【答案】
【分析】
首先根据旋转的性质得出,得出是等边三角形,再证明(SAS),那么四边形的面积即可转化为两个全等三角形的面积,即可求出答案.
【详解】
∵是由旋转得到,
∴,, ,
又∵,,
∴,
∴是等边三角形,,
∴,,
∴,
,
在和中,
∵,
∴(SAS),
∴S四边形=,
故填:.
13.(2021·江苏镇江·二模)如图,在中,,BD平分,将沿折叠,点A落处,则的面积是_____.
【答案】
【分析】
根据折叠,在上,分别求出的面积,即可求出.
【详解】
如图,分别过作垂足分别为
由折叠可知:,
平分
平分,
,
又
故答案为:.
14.(2021·湖南张家界·中考真题)如图,在正方形外取一点,连接,,,过点作的垂线交于点,若,.下列结论:①;②;③点到直线的距离为;④,其中正确结论的序号为______.
【答案】①②④
【分析】
利用同角的余角相等可得∠EDC=∠PDA,利用SAS可证明,可得①正确;②根据全等三角形的性质可得∠APD=∠CED,根据等腰直角三角形的性质可得∠DPE=∠DEP=45°,即可得出∠PEC=90°,可得②正确;过C作CF⊥DE,交DE的延长线于F,利用勾股定理可求出CE的长,根据△DEP是等腰直角三角形,可证△CEF是等腰直角三角形,根据等腰直角三角形的性质即可求出CF的长,可得③错误;④由③可知EF的长,即可得出DF的长,利用勾股定理可求出CD的长,即可求出正方形ABCD的面积,可得④正确,综上即可得答案.
【详解】
∵四边形ABCD为正方形,PD⊥DE,
∴∠PDA+∠PDC=90°,∠EDC+∠PDC=90°,AD=CD,
∴∠EDC=∠PDA,
在△APD和△CED中,
∴△APD≌△CED,故①正确,
∴∠APD=∠DEC,
∵DP=DE,∠PDE=90°,
∴∠DPE=∠DEP=45°,
∴∠APD=∠DEC=135°,
∴∠PEC=∠DEC-∠DEP=90°,
∴AE⊥CE,故②正确,
如图,过C作CF⊥DE,交DE的延长线于F,
∵,∠PDE=90°,
∴PE=,
∵,∠PEC=90°,
∴CE==2,
∵∠DEP=45°,∠PEC=90°,
∴∠FEC=45°,
∵∠EFC=90°,
∴△CEF是等腰直角三角形,
∴CF=EF==,
∴点到直线的距离为,故③错误,
∴DF=EF+DE=+1,
∴CD2===,
∴,故④正确,
综上所述:正确的结论有①②④,
故答案为:①②④
15.(2021·黑龙江龙沙·二模)在△ABC中,AD为∠BAC的角平分线.若添加一个条件:______,则△ABD≌△ACD.
【答案】
【分析】
依据ASA,可知添加的条件可以是AD⊥BC.
【详解】
当AD⊥BC时,∠ADB=∠ADC=90°,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
在△ABD和△ACD中,
,
∴△ABD≌△ACD,
故答案为:AD⊥BC.
16.(2021·山东临沂·一模)如图,的顶点在等边的边上,点在的延长线上,为的中点,连接,若,,则的长为________.
【答案】3
【分析】
根据平行四边形的性质和等边三角形的性质,可以得到和的长,然后可以证明和全等,然后即可得到的长.
【详解】
解:如图,延长交于点,
四边形是平行四边形,
,,,
,,
,,
,
是等边三角形,为的中点,
,,
,
,
在和中,
,
,
,,
,,
,,
,,
是等边三角形,
,
,
故答案为:3.
17.(2021·河南省实验中学三模)如图,在四边形中,平分对角线与边延长线的夹角,,点为中点,若,,则线段的长为________.
【答案】4
【分析】
如图,延长AD交BC延长线于G,利用ASA可证明△ACD≌△GCD,可得AC=CG,AD=GD,根据线段的和差关系可得BG的长,根据点E为AB中点可得DE为△ABG的中位线,根据中位线的性质即可得答案.
【详解】
如图,延长AD交BC延长线于G,
∵平分对角线与边延长线的夹角,,
∴∠ACD=∠GCD,∠ADC=∠GDC=90°,
在△ACD和△GCD中,,
∴△ACD≌△GCD,
∴AC=CG,AD=GD,
∵,,
∴BG=BC+CG=BC+AC=8,
∵点E为AB中点,
∴DE为△ABG的中位线,
∴DE=BG=4,
故答案为:4
三、解答题
18.(2021·山东青岛·中考真题)如图,在中,为边的中点,连接并延长,交的延长线于点,延长至点,使,分别连接,,.
(1)求证:;
(2)当平分时,四边形是什么特殊四边形?请说明理由.
【答案】(1)见解析;(2)矩形,见解析
【分析】
(1)利用平行四边形的性质证明,利用中点的性质证明,结合对顶角相等,从而可得结论;
(2)先证明 结合 证明四边形是平行四边形,再利用等腰三角形的性质证明 从而可得结论.
【详解】
(1)证明:∵四边形是平行四边形,
∴,∴
又∵为边的中点,
∴
∵,,,
∴
(2)答:四边形是矩形,理由如下:
∵四边形是平行四边形,
∴,
∵,
∴,,
∴,
∵,
∴四边形是平行四边形.
∵平分,
∴.
又∵,
∴,
∴
又∵,
∴,
∴,
∴是矩形
19.(2021·山东·日照市田家炳实验中学一模)定义:如果三角形三边的长a、b、c满足,那么我们就把这样的三角形叫做“匀称三角形”.如:三边长分别为1,1,1或3,5,7,…的三角形都是“匀称三角形”.
(1)已知“匀称三角形”的两边长分别为4和6,则第三边长为 .
(2)如图,ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DF⊥AC,垂足为F,交AB的延长线于E,求证:EF是⊙O的切线;
(3)在(2)的条件下,若,判断AEF是否为“匀称三角形”?请说明理由.
【答案】(1)5或8;(2)见解析;(3)AEF是“匀称三角形”,见解析
【分析】
(1)设第三边长为,利用“匀称三角形”的定义,列出方程,但是由于等式中,4,6,均有可能为等式右边的“”,所以需要分三类讨论,最终确定下来的三边长必须满足“三角形两边之和大于第三边”,故最终答案为5或8;
(2)要证明为切线,连接,由于是半径,只需要证明,又由于,所以只需要证明,又由于为中点,只需要证明为的中点,因为是直径,所以,又因为,所以为的中点,即可证明;
(3)因为为的中点,仿照“中线倍长”模型,过作于,如图2,或者在上截取,构造,所以,将转化成,因为,所以,可以得到,设,则,利用勾股定理求出,满足定义,即可证明.
【详解】
解:(1)解:设第三边长为,
①当时,解得,
②当是,解得,
③当时,解得,
,
当三边长为2,4,6时,不能构成三角形,所以③舍去,
故答案为:5或8;
(2)证明:如图1,连接,,
是直径,
,
,
为的中点,即,
为中点,
,,
,
,
,
,
,
是半径,
是的切线;
(3)解:是“匀称三角形”,理由如下:
如图2,过作于,
,
在和中,
,
,
,
,
,
,
,
,
设,则,
,
,
,
是“匀称三角形”.
20.(2021·福建省福州第十九中学三模)如图1,在正方形ABCD中,边长为2a,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.
(1)求证:AF=BE;
(2)如图2,当点E运动到AB中点时,连接DG,求证:DG=2a;
(3)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.
【答案】(1)见解析;(2)见解析;(3)
【分析】
(1)先判断出,再由四边形是正方形,得出,,即可得出结论;
(2)设,先求出,进而得出,再求出,,再判断出,进而判断出,即可得出结论;
(3)先求出,再求出,再判断出,求出,即可得出结论.再证明,求出,即可求出答案.
【详解】
解:(1),
,
,
四边形是正方形,
,,
,
,
,
;
(2)如图2,过点作于,
由题意得:,
点是的中点,
,
,
在中,根据面积相等,得,
,
,
,,
,
,,
,
,
,
,,
,
;
(3)如图3,过点作于,
于点,
,
,
,
在中,,
,
,,
,
,
,
,,
,
,
,
,
.
21.(2021·河南·郑州外国语中学三模)在中,,,在中,,,,连接,,点是的中点,连接.
(1)如图1,当顶点在边上时,线段与线段的数量关系是______,线段与线段的位置关系是 ;
(2)将绕点旋转,转到图2的位置时,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由;
(3)在绕点旋转的过程中,线段的最大值为______;当时,线段的长为______.
【答案】(1),;(2)仍然成立,见解析;(3)或1
【分析】
(1)过点A作,交BC延长线与点G,连接GD并延长交BE于点H,证明∽,得,,再证明CF为的中位线即可证明结论;
(2)与(1)同理可证明结论仍然成立;
(3)延长AF到点K,使,连接BK,通过SAS证明≌,得,在中,利用第三边小于两边之和,得,求出AK最大为4,则AF最大为2即可,当时,由(1)中证明可知,则G,D,E三点共线,分点E在D下方,或点E在点D上方两种情形,分别画图进行计算即可.
【详解】
解:(1)过点A作,交BC延长线与点G,,连接GD并延长交BE于点H,
,,
,
,
,
点C为BG的中点,
,
且,
∽,
,,
,
点C,F分别是BG,BD的中点,
为的中位线,
,,
,
又,
,
,
,
,
故答案为:,,
(2)(1)中结论仍然成立,
过点A作,交BC延长线与点G,,连接GD并延长交BE于点H,设GD交AB于点O,
由(1)同理可证∽,
,,
,
点C,F分别是BG,BD的中点,
为的中位线,
,,
,
又,
,
,
,
,
故答案为:,,
(3)如图,延长AF到点K,使,连接BK,
,,,
≌,
,
在中,
,
,
当时,AF最大为2,
当时,由(2)中证明可知,
,D,E三点共线,如图,当点E在点D下方时,
,,
,
,
,
当点E与G重合时,此时,
,
综上:或,
故答案为:2,1或.
相关试卷
这是一份考点23图形的相似(解析版)-2022年数学中考一轮复习考点透析(北京版),共21页。试卷主要包含了相似图形及比例线段,相似三角形,位似等内容,欢迎下载使用。
这是一份考点23视图与投影(解析版)-2022年数学中考一轮复习考点透析(苏科版),共10页。试卷主要包含了投影,视图等内容,欢迎下载使用。
这是一份考点14全等三角形(解析版)-2022年数学中考一轮复习考点透析(苏科版),共17页。试卷主要包含了三角形全等的判定等内容,欢迎下载使用。










