考点19几何初步及相交线、平行线（解析版）-2022年数学中考一轮复习考点透析（北师大版）

这是一份考点19几何初步及相交线、平行线（解析版）-2022年数学中考一轮复习考点透析（北师大版），共15页。
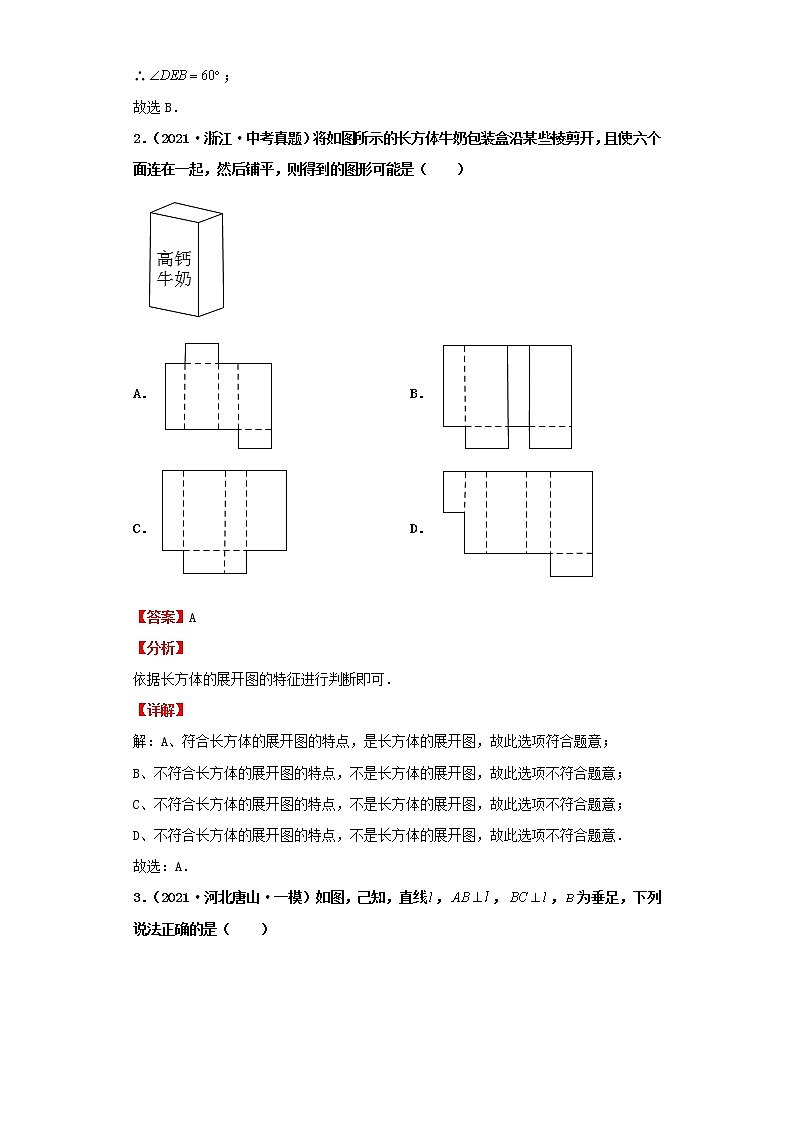
考点19几何初步及相交线、平行线【命题趋势】①角的计算；②角的平分线的意义；③余角；④补角的性质；⑤平行线的性质和判定；⑥命题的相关概念及判断。通常命题以基础题形式考查。【常考知识】①角的计算；②角的平分线的意义；③余角；④补角的性质；⑤平行线的性质和判定；⑥命题的相关概念及判断。【夺分技巧】1、平行线求角度时，注意与三角形的内角和、外角的性质综合。2、涉及由平行线求角度题若出现“拐角”，常从拐角处作平行线，再用平行线的性质解决问题。3、“两点之间，线段最短”，“垂线段最短”在解决最短路径问题时经常用到。 真题演练一、单选题1．（2021·山东济南·中考真题）如图，，，平分，则的度数为（    ）A． B． C． D．【答案】B【分析】由题意易得，然后根据角平分线的定义可得，进而根据平行线的性质可求解．【详解】解：∵，，∴，，∵平分，∴，∴；故选B．2．（2021·浙江·中考真题）将如图所示的长方体牛奶包装盒沿某些棱剪开，且使六个面连在一起，然后铺平，则得到的图形可能是（    ）A． B．C． D．【答案】A【分析】依据长方体的展开图的特征进行判断即可．【详解】解：A、符合长方体的展开图的特点，是长方体的展开图，故此选项符合题意；
B、不符合长方体的展开图的特点，不是长方体的展开图，故此选项不符合题意；
C、不符合长方体的展开图的特点，不是长方体的展开图，故此选项不符合题意；
D、不符合长方体的展开图的特点，不是长方体的展开图，故此选项不符合题意．
故选：A．3．（2021·河北唐山·一模）如图，己知，直线，，，为垂足，下列说法正确的是（    ）A．点到的距离是线段 B．点到点的距离是线段C．、、三点共线 D．、、三点不一定共线【答案】C【分析】逐一进行判断即可．【详解】A. 点A到的距离是线段的长度，故该选项错误；    B. 点到点A的距离是线段的长度，故该选项错误；C. ∵，，∴A、、三点共线，故该选项正确；    D. A、、三点共线，故该选项错误，故选：C．4．（2021·陕西陇县·一模）已知，则的补角为（    ）A． B． C． D．【答案】B【分析】根据两个角的和为180°，两个角互为补角，由此即可解答．【详解】解：∵∠A=75°，∴∠A的补角为:180°-75°=105°．故选B．5．（2021·河北·保定市第十七中学七年级期中）如图，将下面的平面图形绕直线旋转一周，得到的立体图形是（　　）A． B． C． D．【答案】D【分析】根据面动成体，梯形绕下底边旋转是圆锥加圆柱，可得答案.【详解】面动成体，直角三角形绕直角边旋转一周可得圆锥，长方形绕一边旋转一周可得圆柱， 那么所求的图形是下面是圆锥，上面是圆柱的组合图形． 故选D．6．（2021·全国·七年级单元测试）七巧板是中国古代劳动人民的发明，其历史至少可以追溯到公元前一世纪．为祝贺辛丑年的到来，用一副七巧板（如图①），拼成了“牛气冲天”的图案（如图②），则图②中（    ）．A．360° B．270° C．225° D．180°【答案】D【分析】根据七巧板中出现的角的特殊性，得到，，算出结果即可．【详解】解：∵七巧板中的角都是特殊的，出现的角是45°、90°、135°和180°；∴，，∴，故选：D．7．（2021·安徽·合肥市第四十五中学模拟预测）如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，含角的直角三角板的斜边与纸条一边重合，含角的三角板的一个顶点在纸条的另一边上，则的度数是（      ）A． B． C． D．【答案】B【分析】过含角的三角板的直角顶点做一条平行纸条边的线，在图上标出相应的角，利用两直线平行内错角相等，同位角相等，两角互补相关知识求出．【详解】解：过含角的三角板的直角顶点做一条平行纸条边的线，在图上分别标出、、、，由题意及根据两直线平行知：，，所求，由图可知：与互补，，，，故选：B．8．（2021·江苏秦淮·一模）将如图所示的纸片折叠、粘合成正方体形状．下列结论：①粘合时，线段AB与线段FG重合；②在正方体中，DE所在的面与GH所在的面相对；③在正方体中，AC //DE；④在正方体中，DE与EF的夹角是60°．其中所有正确结论的序号是A．①②③ B．①②④ C．①③④ D．②③④【答案】B【分析】根据正方体的平面展开图，折叠成几何体的直观图，直接利用相关性质判定①②③④的结论．【详解】解：根据正方体的平面展开图，折叠成几何体的直观图，如图所示：①粘合时，线段AB与线段FG重合，故①正确，符合题意；②在正方体中，DE所在的面与GH所在的面相对，故②正确，符合题意；③在正方体中，AC 和DE不在同一平面内，不平行，故③错误，不符合题意；④在正方体中，连接BD，所以△BDE为等边三角形，DE与EF所在直线成60°角，故④正确，符合题意．故选：B．9．（2021·河北邱县·七年级期末）如图，的度数可能是（    ）A．50° B．60° C．70° D．120°【答案】C【分析】如图，记量角器所在圆的圆心为过作 再利用角的度量可得答案．【详解】解：如图，记量角器所在圆的圆心为过作
  再观察量角器可得：约为 所以可能为 故选：10．（2021·全国·七年级期末）如图，在直线上的点是（   ）A．点 B．点 C．点 D．点【答案】B【分析】根据图像点与线的关系可直接得出答案．【详解】解：由图像可知点A、C、D在直线外，点B在直线上故选B． 二、填空题11．（2021·浙江·温州绣山中学三模）一个直棱柱的立体图如图所示，该几何体的表面积为____cm2【答案】84【分析】由题意可确定该直棱柱为直三棱柱，则侧面为三个矩形，上下底面为两个相同的三角形，由此计算面积即可．【详解】解：由题意，该直棱柱为直三棱柱，上下底面的三角形三边均为3、4、5，∵，∴该三角形为直角三角形，∴该几何体的表面积为，故答案为：84．12．（2021·山东滨州·中考真题）如图，在中，，，．若点P是内一点，则的最小值为____________．【答案】【分析】根据题意，首先以点A为旋转中心，顺时针旋转△APB到△AP′B′，旋转角是60°，作出图形，然后根据旋转的性质和全等三角形的性质、等边三角形的性质，可以得到PA+PB+PC=PP′+P′B′+PC，再根据两点之间线段最短，可以得到PA+PB+PC的最小值就是CB′的值，然后根据勾股定理可以求得CB′的值，从而可以解答本题．【详解】解：以点A为旋转中心，顺时针旋转△APB到△AP′B′，旋转角是60°，连接BB′、PP′，，如图所示，则∠PAP′=60°，AP=AP′，PB=P′B′，∴△APP′是等边三角形，∴AP=PP′，∴PA+PB+PC=PP′+P′B′+PC，∵PP′+P′B′+PC≥CB′，∴PP′+P′B′+PC的最小值就是CB′的值，即PA+PB+PC的最小值就是CB′的值，∵∠BAC=30°，∠BAB′=60°，AB==2，∴∠CAB′=90°，AB′=2，AC=AB•cos∠BAC=2×cos30°=，∴CB′=，故答案为：．13．（2021·广西玉林·一模）将一块等腰直角三角板与一把直尺如图放置，若，则的大小为________． 【答案】70°【分析】利用平行线的性质以及三角形内角和为180°求解即可．【详解】如图，因为a∥b，所以∠2=∠3，因为∠1=65°，∠4=45°，所以∠3=180°-∠1-∠4=70°，即∠2=70°.故答案为：70°14．（2021·内蒙古呼伦贝尔·中考真题）_______．【答案】【分析】根据度、分、秒的进率计算即可得到答案．【详解】解：，故答案为：．15．（2021·上海·一模）如果两个相似三角形的周长比为，那么它们的对应角平分线的比为_________________．【答案】【分析】结合题意得：；再根据角平分线的性质，通过证明，即可得到答案．【详解】如图，，的角平分线交BC于点N，交PQ于点M∴∵和周长比为∴ ∵的角平分线交BC于点N，交PQ于点M∴ ∴∴故答案为：．16．（2021·辽宁本溪·二模）如图，分别过等边的顶点、作直线、，使得，若，则∠2的度数为_____．
 【答案】80°【分析】利用“两直线平行，同旁内角互补”即可计算出∠2的度数．【详解】解：∵是等边三角形，∴∠BAC=60°．∵a∥b，∴∠2+∠BAC+∠1=180°．∴∠2=180°-∠BAC-∠1=180°-60°-40°=80°．故答案为：80°．17．（2021·广东增城·一模）如图，直线，，则的度数是___________.【答案】50°【分析】由直线a，b被第三条直线所截，a∥b，∠1=130°，两直线平行，同旁内角互补即可求得答案．【详解】解：∵a∥b，∴∠1+∠2=180°，∴∠1=130°，∴∠2=180°-∠1=180°-130°=50°．故答案为：50°．18．（2021·浙江南浔·一模）南浔区某校在开展特色阳光大课间活动中融入了单脚跳跳球运动，如图1，当人单脚跳的过程中，小球会随着球杆绕着脚开始不停的旋转．大课间活动中，五位同学分别站在点处，处同学跳的时候，小球开始在地面上不停旋转形成，如图2为活动过程的俯视示意图，交于点G，，连结，当小球转到点时，，则球杆_______．【答案】100【分析】设AG=x，过F作FH⊥AB，先求出AF=AG=x，AH=x-20，FH=BC=，再根据勾股定理得出，即可得出结论．【详解】解：∵，FC⊥DB， ∴ED∥FC∥AB，设AG=x，过F作FH⊥AB，∴ED=BH=100，FH=BC，AH=AG-HG=x-(100-80)=x-20，∵，∠B=90º，∴AB=DE=AG+BG=x+80，∵，∴BC==，在Rt∆AFH中AF=AG=x，AH=x-20，FH=BC=，，即，解得x=100，即AG=100．故答案为：100．
 19．（2021·上海杨浦·二模）如图，已知在正方形网格中，点A、B、C、D在小正方形的顶点上，线段AB与线段CD相交于点O，那么tan∠AOC＝_____．【答案】3【分析】如图，取格点E、F，连接AE、AF、BE，通过计算得到等腰三角形△ABE，利用等腰三角形的三线合一得出AF⊥BE，接着推出∠AOC＝∠ABF．在Rt△ABF中，由勾股定理求出两直角边的长，再依据正切值的意义可求解．【详解】解：如图，取格点E、F，连接AE、AF、BE，可知AF经过点C，BE经过点F，设网格中的小正方形的边长为1，则AE=AB＝，∵F是BE的中点，∴AF⊥BE．由题意：∠DCB＝∠CBE＝45°．∴CD∥BE，∴∠AOC＝∠ABF．∴tan∠AOC＝tan∠ABF．∵BF＝，AF＝，∴tan∠ABF＝．∴tan∠AOC＝3．故答案为：3．20．（2021·上海闵行·一模）如果港口A的南偏东52°方向有一座小岛B,那么从小岛B观察港口A的方向是________.【答案】北偏西52°    【解析】在A处看小岛B在南偏东的方向上，在B看港口A则在北偏西的方向上，而且角度不变，因此从小岛B观察港口A的方向是北偏西52°，故答案为北偏西52°.