数学冀教版第30章 二次函数综合与测试课时作业

这是一份数学冀教版第30章 二次函数综合与测试课时作业，共30页。试卷主要包含了抛物线y＝42+3的顶点坐标是等内容，欢迎下载使用。

九年级数学下册第三十章二次函数章节练习
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、下列函数中，随的增大而减小的函数是（ ）
A． B． C． D．
2、若函数，则当函数y=15时，自变量的值是（ ）
A． B．5 C．或5 D．5或
3、在抛物线的图象上有三个点，，，则、、的大小关系为（ ）
A． B． C． D．
4、抛物线y＝4(2x﹣3)2+3的顶点坐标是（　　）
A．(，3) B．(4，3) C．(3，3) D．(﹣3，3)
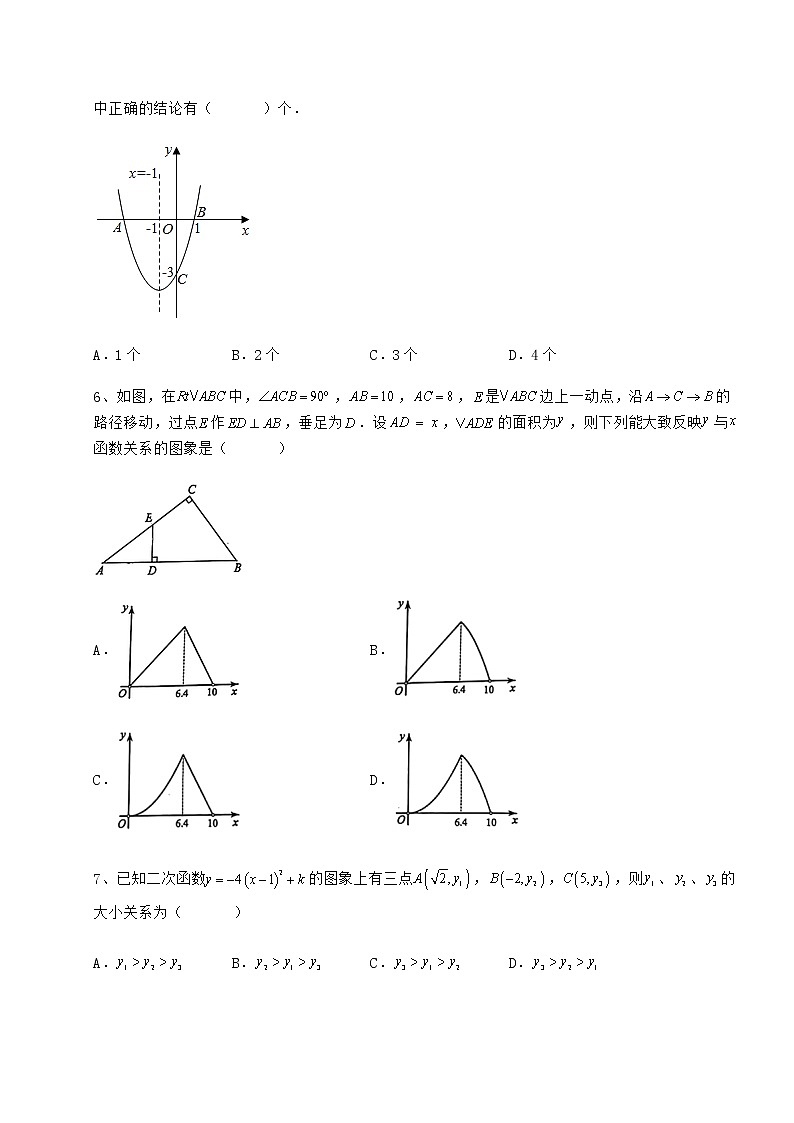
5、如图，二次函数的图象与x轴交于点A、B两点，与y轴交于点C；对称轴为直线，点B的坐标为，则下列结论：①；②；③；④，其中正确的结论有（ ）个．

A．1个 B．2个 C．3个 D．4个
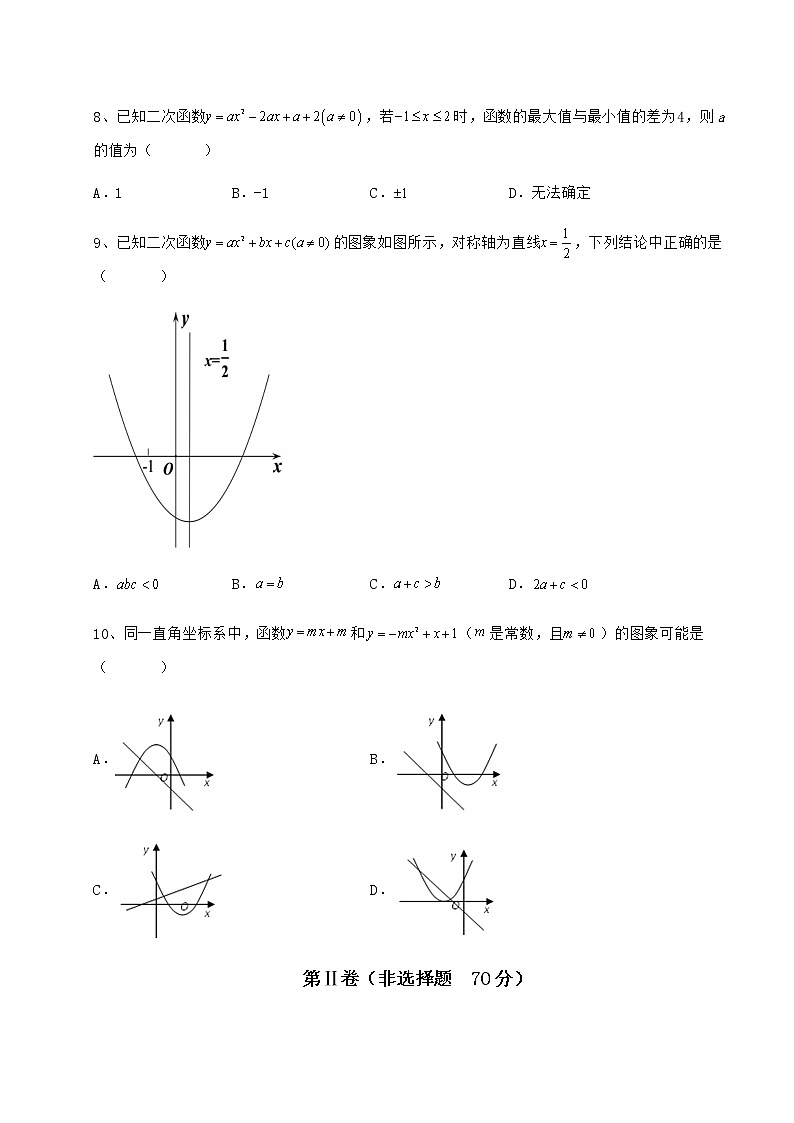
6、如图，在中，，，，是边上一动点，沿的路径移动，过点作，垂足为．设，的面积为，则下列能大致反映与函数关系的图象是（ ）

A． B．
C． D．
7、已知二次函数的图象上有三点，，，则、、的大小关系为（ ）
A． B． C． D．
8、已知二次函数，若时，函数的最大值与最小值的差为4，则a的值为（ ）
A．1 B．-1 C． D．无法确定
9、已知二次函数的图象如图所示，对称轴为直线，下列结论中正确的是（ ）

A． B． C． D．
10、同一直角坐标系中，函数和（是常数，且）的图象可能是（ ）
A． B．
C． D．
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、已知点A（x1，y1）、B（x2，y2）为函数y＝﹣2（x﹣1）2+3的图象上的两点，若x1＜x2＜0，则y1_____y2（填“＞”、“＝”或“＜”），
2、抛物线y＝﹣2（x﹣1）2+4的最高点坐标是_____．
3、将函数的图象向______平移______个单位长度，再向______平移______个单位长度，可以得到函数的图象．
4、二次函数的图像如图所示，对称轴为直线，根据图中信息可求得该二次函数的解析式为______．

5、将抛物线向右平移4个单位，所得到的抛物线的函数解析式是________．
三、解答题（5小题，每小题10分，共计50分）
1、如图，抛物线y＝﹣与x轴交于点A，点B，与y轴交于点C，点D与点C关于x轴对称，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．

(1)求点A、点B、点C的坐标；
(2)求直线BD的解析式；
(3)当点P在线段OB上运动时，直线l交BD于点M，试探究m为何值时，四边形CQMD是平行四边形；
(4)在点P的运动过程中，是否存在点Q，使△BDQ是以BD为直角边的直角三角形？若存在，求出点Q的坐标；若不存在，请说明理由．
2、高邮双黄鸭蛋已入选全世界最值得品尝百种味道，某专卖店根据以往销售数据发现：高邮双黄鸭蛋每天销售数量y（盒）与销售单价x（元/盒）的关系满足一次函数，每盒高邮双黄鸭蛋各项成本合计为40元/盒．
(1)若该专卖店某天获利800元，求销售单价x（元/盒）的值；
(2)当销售单价x定为多少元/盒时，该专卖店每天获利最大？最大利润为多少？
(3)若该专卖店决定每销售一盒就捐出元给当地学校作为贫困学生的助学金，当每天的销售量不低于25盒时，为了确保该店每天扣除捐出后的利润随着销售量的减小而增大，则m的取值范围为______．
3、如图，因疫情防控需要，某校在足够大的空地利用旧墙MN和隔离带围成一个矩形隔离区ABCD，墙长为a米，AD≤MN，矩形隔离区的一边靠墙，其它三边一共用隔离带200米．

(1)a＝30，所围成的矩形隔离区的面积为1800平方米，求所利用旧墙AD的长；
(2)若a＝150．求矩形隔离区ABCD面积的最大值．
4、在平面直角坐标系中，二次函数y＝ax2+bx+c的图象经过点A（0，6）和B（﹣2，﹣2）．

(1)求c的值，并用含a的代数式表示b；
(2)当a＝时．
①求此函数的解析式，并写出当﹣4≤x≤2时，y的最大值和最小值；
②如图，抛物线y＝ax2+bx+c与x轴的左侧交点为C，作直线AC，D为直线AC下方抛物线上一动点，与AC交于点F，作DM⊥AC于点M．是否存在点D使△DMF的周长最大？若存在，请求出D点的坐标；若不存在，请说明理由．
5、如图，二次函数（m是实数，且）的图像与x轴交于A、B两点（点A在点B的左侧），其对称轴与x轴交于点C，已知点D位于第一象限，且在对称轴上，，点E在x轴的正半轴上，．连接ED并延长交y轴于点F，连接AF．

(1)求A、B、C三点的坐标（用数字或含m的式子表示）；
(2)已知点Q在抛物线的对称轴上，当的周长的最小值等于，求m的值．

-参考答案-
一、单选题
1、B
【解析】
【分析】
根据一次函数，反比例函数，二次函数，正比例函数的性质逐项分析即可．
【详解】
A. ，，随的增大而增大，故A选项不符合题意．
B. ，， ，的图像位于第三象限，随的增大而减小，故B选项符合题意；
C. ，，对称轴为轴，在对称轴的左边，随的增大而增大，在对称轴的右边，随的增大而减小，故C选项不符合题意；
D. ，，随的增大而增大，故D选项不符合题意；
故选B．
【点睛】
本题考查了一次函数，反比例函数，二次函数，正比例函数的性质，掌握以上性质是解题的关键．
2、D
【解析】
【分析】
根据题意，利用分类讨论的方法可以求得当函数y=15时，自变量x的值．
【详解】
解：当x＜3时，
令2x2-3=15，
解得x=-3；
当x≥3时，
令3x=15，
解得x=5；
由上可得，x的值是-3或5，
故选：D．
【点睛】
本题考查了二次函数的性质、一次函数的性质，解答本题的关键是明确题意，利用分类讨论的方法解答．
3、C
【解析】
【分析】
把三个点，，的横坐标代入解析式，然后比较函数值大小即可．
【详解】
解：把三个点，，的横坐标代入解析式得，
；；；
所以，，
故选：C．
【点睛】
本题考查了二次函数的性质，解题关键是求出函数值，再比较大小．
4、A
【解析】
【分析】
根据顶点式的顶点坐标为求解即可
【详解】
解：抛物线的顶点坐标是
故选A
【点睛】
本题考查了二次函数顶点式的顶点坐标为，掌握顶点式求顶点坐标是解题的关键．
5、D
【解析】
【分析】
根据二次函数的对称性，以及参数a、b、c的意义即可求出答案．
【详解】
解：∵抛物线的对称轴为x=-1，
所以B（1，0）关于直线x=-1的对称点为A（-3，0），
∴AB=1-（-3）=4，故①正确；
由图象可知：抛物线与x轴有两个交点，
∴Δ=b2-4ac>0，故②正确；
由图象可知：抛物线开口向上，
∴a>0，
由对称轴可知：−<0，
∴b>0，故③正确；
当x=-1时，y=a-b+c<0，故④正确；
所以，正确的结论有4个，
故选：D．
【点睛】
本题考查二次函数，解题的关键是熟练运用二次函数的图象与性质．
6、D
【解析】
【分析】
分两种情况分类讨论：当0≤x≤6.4时，过C点作CH⊥AB于H，利用△ADE∽△ACB得出y与x的函数关系的图象为开口向上的抛物线的一部分；当6.4＜x≤10时，利用△BDE∽△BCA得出y与x的函数关系的图象为开口向下的抛物线的一部分，然后利用此特征可对四个选项进行判断．
【详解】
解：∵，，，
∴BC=，
过CA点作CH⊥AB于H，
∴∠ADE=∠ACB=90°，
∵，
∴CH=4.8，
∴AH=，
当0≤x≤6.4时，如图1，

∵∠A=∠A，∠ADE=∠ACB=90°，
∴△ADE∽△ACB，
∴，即，解得：x=，
∴y=•x•=x2；
当6.4＜x≤10时，如图2，

∵∠B=∠B，∠BDE=∠ACB=90°，
∴△BDE∽△BCA，
∴，
即，解得：x=，
∴y=•x•=；
故选：D．
【点睛】
本题考查了动点问题的函数图象：函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力．解决本题的关键是利用分类讨论的思想求出y与x的函数关系式．
7、A
【解析】
【分析】
分别求出、、的大小，再进行判断即可．
【详解】
解：




A、故选项正确，符合题意；
B、故选项错误，不符合题意；
C、故选项错误，不符合题意；
D、故选项错误，不符合题意．
故选：A．
【点睛】
此题考查了二次函数的大小比较问题，解题的关键是掌握二次函数的性质、利用代入法求出、、的大小．
8、C
【解析】
【分析】
分a＞0或a＜0两种情况讨论，求出y的最大值和最小值，即可求解；
【详解】
当a＞0时，∵对称轴为x=，
当x=1时，y有最小值为2，当x=3时，y有最大值为4a+2，
∴4a+2-2=4．
∴a=1，
当a＜0时，同理可得
y有最大值为2； y有最小值为4a+2，
∴2-(4a+2)=4，
∴a=-1，
综上，a的值为
故选：C
【点睛】
本题考查了二次函数的性质，二次函数图象上点的坐标特征等知识，利用分类思想解决问题是本题的关键．
9、D
【解析】
【分析】
由抛物线的开口方向判断与0的关系，由抛物线与轴的交点判断与0的关系，然后根据对称轴确定的符号，进而对所得结论进行判断．
【详解】
解：图象开口向上，与轴交于负半轴，对称轴在轴右侧，
得到：，，，，
A、，，，得，故选项错误，不符合题意；
B、对称轴为直线，得，解得，故选项错误，不符合题意；
C、当时，得，整理得：，故选项错误，不符合题意；
D、根据图象知，抛物线与轴的交点横坐标，是一正一负，即，根据，整理得：，根据对称性可得出，则，故选项正确，符合题意；
故选：D．
【点睛】
本题主要考查二次函数图象与二次函数系数之间的关系，解题的关键是掌握二次函数系数符号由抛物线开口方向、对称轴、抛物线与轴的交点、抛物线与轴交点的个数确定．
10、D
【解析】
【分析】
根据一次函数，二次函数的图象与性质逐一分析两个解析式中的的符号，再判断即可.
【详解】
解：选项A：由的图象可得：
由的图象可得：则 故A不符合题意；
选项B：由的图象可得：
由的图象可得：则
而抛物线的对称轴为： 则 故B不符合题意；
选项C：由的图象可得：
由的图象可得：则 故C不符合题意；
选项D：由的图象可得：
由的图象可得：则
而抛物线的对称轴为： 则 故D符合题意；
故选D
【点睛】
本题考查的是一次函数与二次函数的图象共存问题，掌握“一次函数与二次函数的图象与性质”是解本题的关键.
二、填空题
1、＜
【解析】
【分析】
找到二次函数对称轴，根据二次函数的增减性即可得出结论．
【详解】
解：∵y＝﹣2（x﹣1）2+3，
∴抛物线y＝﹣2（x﹣1）2+3的开口向下，对称轴为x＝1，
∴在x＜1时，y随x的增大而增大，
∵x1＜x2＜0，
∴y1＜y2．
故答案为：＜．
【点睛】
本题考查二次函数的增减性，掌握其增减规律，找到对称轴是解本题关键．
2、
【解析】
【分析】
根据，顶点坐标是，可得答案．
【详解】
解：抛物线为，
开口向下，则最高点坐标是顶点坐标，
顶点坐标．
故答案为：．
【点睛】
本题考查了二次函数的性质以及顶点式，解题的关键是准确理解顶点式．
3、 左 1 下 2
【解析】
【分析】
根据二次函数平移的性质解答．
【详解】
解：∵函数的图象向左平移1个单位长度，再向下平移2个单位长度，可以得到函数的图象．
故答案为：左，1，下，2．
【点睛】
此题考查了二次函数图象平移的性质：上加下减，左加右减，熟记性质是解题的关键．
4、y=－x2－2x+3
【解析】
【分析】
根据图象与x、y轴的交点坐标和对称轴，利用待定系数法求二次函数的解析式即可．
【详解】
解：设该二次函数的解析式为y=ax2+bx+c（a≠0），
由图象知：当x=1时，y=0，当x=0时，y=3，又对称轴为直线x=－1，
则，解得：，
∴该二次函数的解析式为y=－x2－2x+3，
故答案为：y=－x2－2x+3．
【点睛】
本题考查二次函数的图象与性质、待定系数法求二次函数的解析式，熟练掌握待定系数法求二次函数的解析式是解答的关键．
5、y=（x-4）2
【解析】
【分析】
先确定出原抛物线的顶点坐标，然后根据向右平移横坐标加，向下平移纵坐标减求出新图象的顶点坐标，然后写出即可．
【详解】
解：抛物线y=x2的顶点坐标为（0，0），
向右平移4个单位后的图象的顶点坐标为（4，0），
所以，所得图象的解析式为y=（x-4）2，
故答案为：y=（x-4）2．
【点睛】
本题主要考查的是函数图象的平移，根据平移规律“左加右减，上加下减”利用顶点的变化确定图形的变化是解题的关键．
三、解答题
1、 (1)A（﹣1，0），B（4，0），C（0，2）
(2)y＝x﹣2
(3)当m＝2时，四边形CQMD是平行四边形
(4)存在，（3，2），（8，﹣18），（﹣1，0）
【解析】
【分析】
（1）根据函数解析式列方程即可得到结论；
（2）由点C与点D关于x轴对称，得到D（0，﹣2），解方程即可得到结论；
（3）如图1所示：根据平行四边形的性质得到QM＝CD，设点Q的坐标为（m，﹣m2+m+2），则M（m，m﹣2），列方程即可得到结论；
（4）设点Q的坐标为（m，﹣m2+m+2），分两种情况：①当∠QBD＝90°时，根据勾股定理列方程求得m＝3，m＝4（不合题意，舍去），②当∠QDB＝90°时，根据勾股定理列方程求得m＝8，m＝﹣1，于是得到结论．
(1)
解：∵令x＝0得；y＝2，
∴C（0，2）．
∵令y＝0得：﹣x2+x+2＝0，
解得：x1＝﹣1，x2＝4．
∴A（﹣1，0），B（4，0）．
(2)
解：∵点C与点D关于x轴对称，
∴D（0，﹣2）．
设直线BD的解析式为y＝kx﹣2．
∵将（4，0）代入得：4k﹣2＝0，
∴k＝．
∴直线BD的解析式为y＝x﹣2．
(3)
解：如图1所示：

∵，
∴当QM＝CD时，四边形CQMD是平行四边形．
设点Q的坐标为（m，﹣m2+m+2），
则M（m，m﹣2），
∴﹣m2+m+2﹣（m﹣2）＝4，
解得：m＝2，m＝0（不合题意，舍去），
∴当m＝2时，四边形CQMD是平行四边形；
(4)
解：存在，设点Q的坐标为（m，﹣m2+m+2），
∵△BDQ是以BD为直角边的直角三角形，
∴①当∠QBD＝90°时，
由勾股定理得：BQ2+BD2＝DQ2，
即（m﹣4）2+（﹣m2+m+2）2+20＝m2+（﹣m2+m+2+2）2，
解得：m＝3，m＝4（不合题意，舍去），
∴Q（3，2）；
②当∠QDB＝90°时，
由勾股定理得：BQ2＝BD2+DQ2，
即（m﹣4）2+（﹣m2+m+2）2＝20+m2+（﹣m2+m+2+2）2，
解得：m＝8，m＝﹣1，
∴Q（8，﹣18），（﹣1，0），
综上所述：点Q的坐标为（3，2），（8，﹣18），（﹣1，0）．
【点睛】
此题考查了求抛物线与坐标轴的交点，求一次函数的解析式，平行四边形的性质，解一元二次方程，勾股定理的应用，解题的关键是理解题意，综合掌握各知识点并应用解决问题．
2、 (1)60或80
(2)当销售单价x定70元/盒时，该专卖店每天获利最大，最大利润，900元
(3)
【解析】
【分析】
（1）利用利润等于每天的销售额减去总成本，列出方程，即可求解；
（2）设该专卖店每天获利 元，根据题意，列出函数关系式，再根据二次函数的性质，即可求解；
（3）设该店每天扣除捐出后的利润为 元，每天销售量为 盒，则每盒的销售单价为元/盒 ，每盒的利润为 元，根据题意列出关于的函数关系式，再根据二次函数的性质，即可求解．
(1)
解：根据题意得：
，
解得： ，
答：若该专卖店某天获利800元，销售单价为60或80元/盒；
(2)
解：设该专卖店每天获利 元，根据题意得：
，
∴当销售单价x定70元/盒时，该专卖店每天获利最大，最大利润，900元；
(3)
解：设该店每天扣除捐出后的利润为 元，每天销售量为 盒，则每盒的销售单价为元/盒 ，每盒的利润为 元，根据题意得：
，
∵ ，
∴该图象开口向下，对称轴为： ，
根据题意得：当 时， 随 的减小而增大，
∴ ，解得： ，
∵ ，
∴m的取值范围为 ．
【点睛】
本题主要考查了一元二次方程的应用，二次函数的应用，明确题意，准确得到等量关系是解题的关键．
3、 (1)AD=20米；
(2)当x=100时，S最大=5000米2．
【解析】
【分析】
（1）设AD=x，AB=(200-x)÷2=100-，根据长方形面积公式列方程，解方程，根据墙长得出AD=20米；
（2）矩形隔离区ABCD面积用S表示，根据长方形面积公式列出面积函数S=x100-12x然后配方为S即可．
(1)
解：设AD=x，AB=(200-x)÷2=100-，
∴根据题意得：，
整理得，
解得：，
∵a＝30，
∴AD=20米；
(2)
解：矩形隔离区ABCD面积用S表示，
则S=，
∵a＝150＞100，
∴当x=100时，S最大=5000米2．
【点睛】
本题考查长方形面积，列一元二次方程解图形问题应用题，列二次函数解图形问题的最值问题，掌握长方形面积，列一元二次方程解图形问题应用题，列二次函数解图形问题的最值问题是解题关键．
4、 (1)c=6；b=2a+4
(2)①最小值为−，最大值为20；②D(−3，−)．
【解析】
【分析】
（1）分别把 A（0，6）和B（-2，-2）代入解析式，可得c和b的值．
（2）①当a＝时，此函数表达式为y＝x2+x+6，图象开口向上，由顶点坐标公式可知顶点坐标，根据二次函数的性质，当在顶点时函数值最小观察图象结合增减性，当x=2时，y有最大值．②令y=0，得C的坐标，设直线AC的解析式为y=kx+m，把A（0，6），C（-6，0）代入可得直线AC解析式，设D(x，x2+x+6)则F（x，x+6），得FD的值，设△FDM的周长为l，则l＝DF+DM+MF＝，当FD最大时，周长最大，根据二次函数的性质可得最大值．
(1)
把（0，6）代入y=ax2+bx+c，
得c=6．
把（-2，-2）代入y=ax2+bx+6，
得4a-2b+6=-2，
∴b=2a+4．
(2)
①当a＝时，
∴，且c=6
∴函数表达式为y＝x2+x+6=，图象开口向上．
∴顶点坐标为，

∵-4≤x≤2，
∴当x＝−时，y的最小值为−．
观察图象结合增减性，当x=2时，y有最大值，
把x=2代入y＝x2+x+6，
y的最大值为20．
②∵y＝x2+x+6，
令y=0，则x=-6或x＝−，
∵点C在左侧，
∴C（-6，0）
设直线AC的解析式为y=kx+m，
把A（0，6），C（-6，0）代入y=kx+m，得
m=6-6k+m=0
解得k=1，m=6，
∴y=x+6
设D(x，x2+x+6)则F（x，x+6）
∴FD＝x+6−(x2+x+6)＝−x2−x，
∵OA=OC=6，∠AOC=90°，
∴∠COA=90°，
∵DF∥AO，
∴∠DFM=∠CAO=45°，
DM＝FM＝FD，
设△FDM的周长为l，
则l＝DF+DM+MF＝
当FD最大时，周长最大，
又∵，
又∵−＜0且-6＜x＜0，
∴x=-3时，FD有最大值，即此刻△FDM周长最大．
把x=-3代入y＝x2+x+6，
得y＝−，
∴D(−3，−)．
【点睛】
本题考查二次函数的应用，解本题要熟练掌握二次函数的性质，求二次函数的解析式、待定系数法，数形结合是解题关键．
5、 (1)，，
(2)
【解析】
【分析】
（1）把代入函数解析式，可得，再利用因式分解法解方程可得的坐标，再求解函数的对称轴，可得的坐标；
（2）先证明，利用相似三角形的性质求解，利用三角形的中位线定理再求解．再利用勾股定理求解，如图，当点、、三点共线时，的长最小，此时的周长最小．可得．再利用勾股定理列方程，解方程可得答案．
(1)
令 则，


∴，，
∴对称轴为直线，
∴．
(2)
在中，

，
∴∠ODC=∠CBD，
，


，．
．
∵轴，轴，
∴．
∵，
∴．
∴．
在中，，
∴，即．（负根舍去）
∵点与点关于对称轴对称，
∴．
∴如图，当点、、三点共线时，的长最小，此时的周长最小．
∴的周长的最小值为，

∴的长最小值为，即．
∵，
∴．
∴．
∵，
∴．
【点睛】
本题考查了二次函数与坐标轴的交点问题，二次函数图象的性质，相似三角形的性质与判定，勾股定理，根据对称性求最值，掌握二次函数图象的性质是解题的关键．