2021学年第十三章 相交线 平行线综合与测试一课一练

这是一份2021学年第十三章 相交线 平行线综合与测试一课一练，共30页。试卷主要包含了下列命题正确的是，直线m外一点P它到直线的上点A等内容，欢迎下载使用。
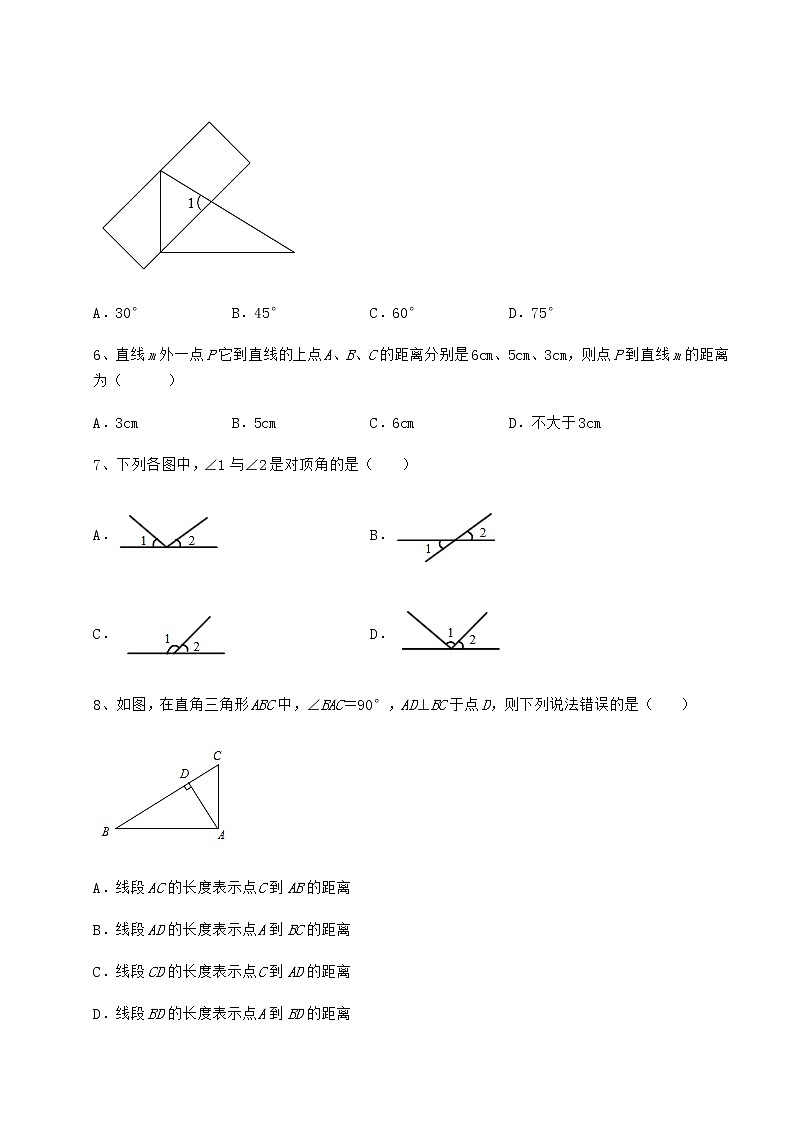
七年级数学第二学期第十三章相交线 平行线难点解析 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、下列说法：①和为180°且有一条公共边的两个角是邻补角；②过一点有且只有一条直线与已知直线垂直；③同位角相等；④经过直线外一点，有且只有一条直线与这条直线平行，其中正确的有（    ）A．0个 B．1个 C．2个 D．3个2、如图，直线，相交于点，，，平分，给出下列结论：①当时，；②为的平分线；③若时，；④．其中正确的结论有（    ）A．4个 B．3个 C．2个 D．1个3、如图所示，直线l1l2，∠1和∠2分别为直线l3与直线l1和l2相交所成角．如果∠1＝52°，那么∠2＝（　　）A．138° B．128° C．52° D．152°4、下列命题正确的是（　　）（1）两条直线被第三条直线所截，同位角相等；（2）在同一平面内，过一点有且只有一条直线与已知直线垂直；（3）平移前后连接各组对应点的线段平行且相等；（4）从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离；（5）在同一平面内，三条直线的交点个数有三种情况．A．0个 B．1个 C．2个 D．3个5、如图，直尺的一条边经过直角三角尺的直角顶点且平分直角，它的对边恰巧经过60°角的顶点．则∠1的大小是（　　）A．30° B．45° C．60° D．75°6、直线m外一点P它到直线的上点A、B、C的距离分别是6cm、5cm、3cm，则点P到直线m的距离为（      ）A．3cm B．5cm C．6cm D．不大于3cm7、下列各图中，∠1与∠2是对顶角的是（　　）A． B．C． D．8、如图，在直角三角形ABC中，∠BAC＝90°，AD⊥BC于点D，则下列说法错误的是（　　）A．线段AC的长度表示点C到AB的距离B．线段AD的长度表示点A到BC的距离C．线段CD的长度表示点C到AD的距离D．线段BD的长度表示点A到BD的距离9、下列各图中，∠1与∠2是对顶角的是（      ）A．  B． C．  D．10、如图，若AB∥CD，CD∥EF，那么BCE＝（    ）A．180°－2＋1 B．180°－1－2 C．2＝21 D．1＋2第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、如图，点O在直线AB上，OD⊥OE，垂足为O．OC是∠DOB的平分线，若∠AOD=70°，则∠COE=__________度．2、如图，直线AB和直线CD相交于点O，且∠AOC＝2∠BOC，则∠AOD的度数为____________．3、如图，点C到直线AB的距离是线段 ___的长．4、如图，∠AOB＝90°，则AB___BO；若OA＝3cm，OB＝2cm，则A点到OB的距离是________cm，点B到OA的距离是________cm；O点到AB上各点连接的所有线段中________最短．5、如图，过直线AB上一点O作射线OC、OD ，并且OD是∠ AOC的平分线，∠BOC=29°18′，  则∠BOD的度数为___________．三、解答题（10小题，每小题5分，共计50分）1、如图所示，从标有数字的角中找出：(1)直线CD和AB被直线AC所截构成的内错角.(2)直线CD和AC被直线AD所截构成的同位角.(3)直线AC和AB被直线BC所截构成的同旁内角.2、如图，直线相交于点平分．（1）若，求∠BOD的度数；（2）若，求∠DOE的度数．3、如图，∠AGB＝∠EHF，∠C＝∠D．（1）求证：BD∥CE；（2）求证：∠A＝∠F．4、如图，已知，，，试说明直线AD与BC垂直（请在下面的解答过程的空格内填空或在括号内填写理由）．理由：C，（已知）                  ，（             ）          ．（             ）又，（已知）        =180°．（等量代换）                  ，（             ）．（             ），（已知），                  ．5、将一个含有60°角的三角尺ABC的直角边BC放在直线MN上，其中∠ABC＝90°，∠BAC＝60°．点D是直线MN上任意一点，连接AD，在∠BAD外作∠EAD，使∠EAD＝∠BAD．（1）如图，当点D落在线段BC上时，若∠BAD＝18°，求∠CAE的度数；（2）当点E落在直线AC上时，直接写出∠BAD的度数；（3）当∠CAE：∠BAD＝7：4时，直接写出写∠BAD的度数．6、根据解答过程填空（写出推理理由或数学式）：如图，已知∠DAF＝∠F，∠B＝∠D，试说明AB∥DC．证明：∵∠DAF＝∠F（已知）．∴AD∥BF（ 　   　），∴∠D＝∠DCF（ 　   　）．∵∠B＝∠D（已知），∴（ 　   　）＝∠DCF（等量代换），∴AB∥DC（ 　   　）．7、如图，在中，平分交于D，平分交于F，已知，求证：．8、如图直线，直线与分别和交于点交直线b于点C．（1）若，直接写出     ；（2）若，则点B到直线的距离是      ；（3）在图中直接画出并求出点A到直线的距离．9、如图，∠ENC+∠CMG=180°，AB∥CD．（1）求证：∠2=∠3．（2）若∠A=∠1+70°，∠ACB=42°，则∠B的大小为______．10、已知：如图，BC，AF是直线，AD∥BC，∠1＝∠2，∠3＝∠求证：AB∥CD．证明：∵AD∥BC（已知），∴∠3＝　   　（ 　   　）．∵∠3＝∠4（已知），∴∠4＝　   　（ 　   　）．∵∠1＝∠2（已知），∴∠1+∠CAF＝∠2+∠CAF（ 　   　）．即∠BAF＝　   　．∴∠4＝∠BAF．（ 　   　）．∴AB∥CD（ 　   　）．4．如图，点O是直线AB上的一点，∠BOC：∠AOC＝1：2，OD平分∠BOC，OE⊥OD于点O．（1）求∠BOC的度数；（2）试说明OE平分∠AOC． -参考答案-一、单选题1、B【分析】根据举反例可判断①，根据垂线的定义可判断②，根据举反例可判断③，根据平行线的基本事实可判断④．【详解】解：①如图∠AOC=∠2=150°，∠BOC=∠1=30°，满足∠1+∠2=180°，射线OC是两角的共用边，但∠1与∠2不是邻补角，故①不正确；②在同一个面内，过一点有且只有一条直线与已知直线垂直，故②不正确；③如图直线a、b被直线c所截，∠1与∠2是同位角，但∠1＞∠2，故③不正确；④经过直线外一点，有且只有一条直线与这条直线平行，是基本事实，故④正确；其中正确的有④一共1个．故选择B．【点睛】本题考查基本概念的理解，掌握基本概念是解题关键．2、B【分析】由邻补角，角平分线的定义，余角的性质进行依次判断即可．【详解】解：∵∠AOE=90°，∠DOF=90°，∴∠BOE=90°=∠AOE=∠DOF，∴∠AOF+∠EOF=90°，∠EOF+∠EOD=90°，∠EOD+∠BOD=90°，∴∠EOF=∠BOD，∠AOF=∠DOE，∴当∠AOF=50°时，∠DOE=50°；故①正确；∵OB平分∠DOG，∴∠BOD=∠BOG，∴∠BOD=∠BOG=∠EOF=∠AOC，故④正确；∵，∴∠BOD=180°-150°=30°，∴故③正确；若为的平分线，则∠DOE=∠DOG，∴∠BOG+∠BOD=90°-∠EOE，∴∠EOF=30°，而无法确定，∴无法说明②的正确性；故选：B．【点睛】本题考查了邻补角，角平分线的定义，余角的性质，数形结合是解决本题的关键．3、B【分析】根据两直线平行同位角相等，得出∠1＝∠3＝52°．再由∠2与∠3是邻补角，得∠2＝180°﹣∠3＝128°．【详解】解：如图．∵l1//l2，∴∠1＝∠3＝52°．∵∠2与∠3是邻补角，∴∠2＝180°﹣∠3＝180°﹣52°＝128°．故选：B．【点睛】本题主要考查了平行线的性质、邻补角的定义，熟练掌握平行线的性质、邻补角的定义是解决本题的关键．4、B【分析】根据平行线的性质、垂直的定义、平移的性质、点到直线的距离的定义、直线的位置关系逐个判断即可得．【详解】解：（1）两条平行线被第三条直线所截，同位角相等；则原命题错误；（2）在同一平面内，过一点有且只有一条直线与已知直线垂直；则原命题正确；（3）平移前后连接各组对应点的线段平行（或在同一条直线上）且相等；则原命题错误；（4）从直线外一点到这条直线的垂线段的长度，叫做这点到这条直线的距离；则原命题错误；（5）在同一平面内，三条直线的交点个数可能为0个或1个或2个或3个，共有四种情况；则原命题错误；综上，命题正确的是1个，故选：B．【点睛】本题考查了平行线的性质、垂直的定义、平移的性质、点到直线的距离的定义、直线的位置关系，熟练掌握各定义和性质是解题关键．5、D【分析】由AC平分∠BAD，∠BAD=90°，得到∠BAC=45°，再由BD∥AC，得到∠ABD=∠BAC=45°，∠1+∠CBD=180°，由此求解即可．【详解】解：∵AC平分∠BAD，∠BAD=90°，∴∠BAC=45°∵BD∥AC，∴∠ABD=∠BAC=45°，∠1+∠CBD=180°，∵∠CBD=∠ABD+∠ABC=45°+60°=105°，∴∠1=75°，故选D．【点睛】本题主要考查了平行线的性质和角平分线的定义，解题的关键在于能够熟练掌握平行线的性质．6、D【分析】根据垂线段的性质“直线外和直线上所有点的连线中，垂线段最短”作答．【详解】解：垂线段最短，点到直线的距离，故选：D．【点睛】本题考查了点到直线的距离的定义和垂线段的性质，解题的关键是掌握垂线段最短．7、B【分析】根据对顶角的定义作出判断即可．【详解】解：根据对顶角的定义可知：只有B选项的是对顶角，其它都不是．故选：B．【点睛】本题考查对顶角的定义，解题关键是明确两条直线相交后所得的只有一个公共顶点且两边互为反向延长线，这样的两个角叫做对顶角．8、D【分析】根据直线外一点，到这条直线的垂线段的长度是这点到直线的距离判断即可．【详解】解：A. 线段AC的长度表示点C到AB的距离，说法正确，不符合题意；B. 线段AD的长度表示点A到BC的距离，说法正确，不符合题意；C. 线段CD的长度表示点C到AD的距离，说法正确，不符合题意；D. 线段BD的长度表示点B到AD的距离，原说法错误，符合题意；故选：D．【点睛】本题考查了点到直线的距离，解题关键是准确识图，正确进行判断．9、C【分析】根据对顶角的定义作出判断即可．【详解】解：根据对顶角的定义可知：只有C选项的是对顶角，其它都不是．故选C．【点睛】本题考查对顶角的定义，两条直线相交后所得的只有一个公共顶点且两边互为反向延长线，这样的两个角叫做对顶角．10、A【分析】根据两直线平行，内错角相等，同旁内角互补，这两条性质解答．【详解】∵AB∥CD，CD∥EF，∴∠1=∠BCD，∠ECD+∠2=180°，∴BCE＝∠BCD+∠ECD=180°－2＋1，故选A．【点睛】本题考查了平行线的性质，正确选择合适的平行线性质是解题的关键．二、填空题1、35【分析】根据补角的性质，可得∠BOD=110°，再由OC是∠DOB的平分线，可得 ，又由OD⊥OE，可得到∠BOE=20°，即可求解．【详解】解：∵∠AOD=70°，∠AOD+∠BOD=180°，∴∠BOD=110°，∵OC是∠DOB的平分线，∴ ，∵OD⊥OE，∴∠DOE=90°，∴∠BOE=∠BOD-∠DOE=20°，∴∠COE=∠BOC-∠BOE=35°．故答案为：35【点睛】本题主要考查了补角的性质，角平分线的定义，角的和与差，熟练掌握补角的性质，角平分线的定义，角的和与差运算是解题的关键．2、【分析】根据，可得，再根据对顶角相等即可求出的度数．【详解】解：∵，∴∴∵∴故答案为：【点睛】本题主要考查了邻补角、对顶角的相关知识，熟练运用邻补角、对顶角的相关知识是解答此题的关键．3、CF【分析】根据点到直线的距离的定义即可求解．【详解】∵CF⊥BF，∴点到直线的距离是线段CF的长故答案为：CF．【点睛】此题主要考查点到直线的距离的判断，解题的关键是熟知点到直线的距离需要作垂线．4、＞    3    2    垂线段    【分析】根据点到直线的距离的定义，大角对大边，垂线段最短进行求解即可．【详解】解：∵∠AOB＝90°，∴AO⊥BO，AB＞BO，∵OA＝3cm，OB＝2cm，∴A点到OB的距离是3cm，点B到OA的距离是2cm，O点到AB上各点连接的所有线段中垂线段最短，故答案为：＞，3，2，垂线段．【点睛】本题主要考查了点到直线的距离，大角对大边，垂线段最短，解题的关键在于能够熟知相关定义．5、【分析】先求出的度数，再根据角平分线的运算可得的度数，然后根据角的和差即可得．【详解】解：，，是的平分线，，，故答案为：．【点睛】本题考查了邻补角、与角平分线有关的计算，熟记角的运算法则是解题关键．三、解答题1、 (1)直线CD和AB被直线AC所截构成的内错角是∠2和∠5； (2)直线CD和AC被直线AD所截构成的同位角是∠1和∠7；(3)直线AC和AB被直线BC所截构成的同旁内角是∠3和∠4【分析】根据两条直线被第三条直线所截，所形成的角中，两角在两条直线的中间，第三条直线的两旁，可得内错角，两角在两直线的中间，第三条直线的同侧，可得同旁内角，两角在两条直线的同侧，第三条直线的同侧，可得同位角.【详解】解：(1)直线CD和AB被直线AC所截构成的内错角是∠2和∠5.(2)直线CD和AC被直线AD所截构成的同位角是∠1和∠7.(3)直线AC和AB被直线BC所截构成的同旁内角是∠3和∠4.【点睛】此题主要考查了三线八角，关键是掌握同位角的边构成F形，内错角的边构成Z形，同旁内角的边构成U形．2、（1）20°；（2）60°【分析】（1）先求出∠AOF=140°，然后根据角平分线的定义求出∠AOC=70°，再由垂线的定义得到∠AOB=90°，则∠BOD=180°-∠AOB-∠AOC=20°；（2）先求出∠AOE=60°，从而得到∠AOF=120°，根据角平分线的性质得到∠AOC =60°，则∠COE=∠AOE+∠AOC=120°，∠DOE=180°-∠COE=60°．【详解】解：（1）∵∠AOE=40°，∴∠AOF=180°-∠AOE=140°，∵OC平分∠AOF，∴∠AOC=∠AOF=70°，∵OA⊥OB，∴∠AOB=90°，∴∠BOD=180°-∠AOB-∠AOC=20°；（2）∵∠BOE=30°，OA⊥OB，∴∠AOE=60°，∴∠AOF=180°-∠AOE=120°，∵OC平分∠AOF，∴∠AOC=∠AOF=60°，∴∠COE=∠AOE+∠AOC=60°+60°=120°，∴∠DOE=180°-∠COE=60°．【点睛】本题主要考查了几何中角度的计算，角平分线的定义，垂线的定义，解题的关键在于能够熟练掌握角平分线的定义．3、（1）证明见解析；（2）证明见解析．【分析】（1）由∠AGB＝∠1，∠AGB＝∠EHF，可得∠1＝∠EHF，则BD∥CE；（2）由BD∥CE，可得∠D＝∠2，则∠2＝∠C，推出AC∥DF，则∠A＝∠F．【详解】证明：（1）∵∠AGB＝∠1，∠AGB＝∠EHF，∴∠1＝∠EHF，∴BD∥CE；（2）∵BD∥CE，∴∠D＝∠2，∵∠D＝∠C，∴∠2＝∠C，∴AC∥DF，∴∠A＝∠F．【点睛】本题主要考查了平行线的性质与判定，对顶角相等，熟练掌握平行线的性质与判定条件是解题的关键．4、GD；AC；同位角相等，两直线平行；；两直线平行，内错角相等；；AD；EF；同旁内角互补，两直线平行；两直线平行，同位角相等；AD；BC【分析】结合图形，根据平行线的判定和性质逐一进行填空即可．【详解】解：，已知，同位角相等，两直线平行两直线平行，内错角相等又，（已知）（等量代换），同旁内角互补，两直线平行）（两直线平行，同位角相等），（已知） ，，．【点睛】本题主要考查了平行线的判定和性质，垂线的定义，解答此题的关键是注意平行线的性质和判定定理的综合运用．5、（1）；（2）；（3）的值为：或.【分析】（1）先求解 再利用角的和差关系可得答案；（2）分两种情况讨论，当落在的下方时，如图，当落在的上方时，如图，再结合已知条件可得答案；（3）分两种情况讨论，如图，当落在的内部时，如图，当落在的外部时，再利用角的和差倍分关系可得答案.【详解】解：（1） ∠BAD＝18°，∠EAD＝∠BAD， （2）当落在的下方时，如图， 当落在的上方时，如图， 而 （3）当落在的内部时，如图， ∠CAE：∠BAD＝7：4, 当落在的外部时，如图， ∠CAE：∠BAD＝7：4,设则 解得： 综上：的值为：或.【点睛】本题考查的是角的和差倍分关系，周角的含义，邻补角的含义，三角形中的角度问题，一元一次方程的应用，根据题干信息画出符合题意的图形，再进行分类讨论是解本题的关键.6、内错角相等，两直线平行；两直线平行，内错角相等；∠B；同位角相等，两直线平行．【分析】根据平行线的性质与判定条件完成证明过程即可．【详解】证明：∵∠DAF＝∠F（已知）．∴AD∥BF（内错角相等，两直线平行），∴∠D＝∠DCF（两直线平行，内错角相等）．∵∠B＝∠D（已知），∴∠B＝∠DCF（等量代换），∴AB∥DC（同位角相等，两直线平行）．故答案为：内错角相等，两直线平行；两直线平行，内错角相等；∠B；同位角相等，两直线平行．【点睛】本题主要考查了平行线的性质与判定，熟知平行线的性质与判定条件是解题的关键．7、见解析【分析】根据∠ADE=∠B可判定DE∥BC，根据平行线的性质得到∠ACB=∠AED，再根据角平分线的定义推出∠ACD=∠AEF，即可判定EF∥CD．【详解】证明：（已知），（同位角相等，两直线平行），（两直线平行，同位角相等），平分，平分（已知），，（角平分线的定义），（等量代换）.（同位角相等，两直线平行）.【点睛】此题考查了平行线的判定与性质，以及角平分线的定义，熟练掌握平行线的判定与性质是解题的关键．8、（1）；（2）4；（3）作图见详解；点A到直线BC的距离为．【分析】（1）根据平行线的性质：两直线平行，同旁内角互补及垂直的性质即可得；（2）根据点到直线的距离可得点B到直线AC的距离为线段，由此即可得出结果；（3）过点A作，点A到直线BC的距离为线段AD的长度，利用三角形等面积法即可得出．【详解】解：（1）∵，∴，∵，，∴，故答案为：；（2）∵，∴点B到直线AC的距离为线段，故答案为：4；（3）如图所示：过点A作，点A到直线BC的距离为线段AD的长度，∵，∴为直角三角形， ∴，即，解得：，∴点A到直线BC的距离为．【点睛】题目主要考查平行线的性质及点到直线的距离，熟练掌握等面积法求距离是解题关键．9、（1）见解析；（2）34°【分析】（1）根据对顶角相等可得出∠ENC+∠FMN=180°，根据平行线的判定可得FG∥ED，由平行线的性质可得∠2=∠D，∠3=∠D，等量代换即可得出结论；（2）由平行线的性质∠A+∠ACD=180°，结合已知可得∠1+70°+∠1+42°=180°，可求得∠1=34°，根据平行线的性质即可求解．【详解】（1）证明：∵∠ENC+∠CMG=180°，∠CMG=∠FMN，∴∠ENC+∠FMN=180°，∴FG∥ED，∴∠2=∠D，∵AB∥CD，∴∠3=∠D，∴∠2=∠3；（2）解：∵AB∥CD，∴∠A+∠ACD=180°，∵∠A=∠1+70°，∠ACB=42°，∴∠1+70°+∠1+42°=180°，∴∠1=34°，∵AB∥CD，∴∠B=∠1=34°．故答案为：34°．【点睛】本题主要考查了平行线的性质与判定定理，解答此题的关键是注意平行线的性质和判定定理的综合运用．10、（1）∠BOC＝60°（2）见解析【分析】（1）根据∠AOB是平角，∠BOC：∠AOC＝1：2即可求解；（2）由角平分线的定义和相加等于90°的两个角互余、等角的余角相等来分析即可．【详解】（1）∵∠AOB＝∠BOC+∠AOC＝180°，又∠BOC：∠AOC＝1：2，∴∠AOC＝2∠BOC，∴∠BOC+2∠BOC＝180°，∴∠BOC＝60°；（2）∵OD平分∠BOC，∴∠BOD＝∠DOC，∵∠DOC+∠COE＝90°，∠AOB是平角，∴∠AOE+∠BOD＝90°，∴∠AOE＝∠COE即OE平分∠AOC．【点睛】本题考查了角的计算和角平分线的定义，垂直的定义，正确理解角平分线的定义，余角的性质以及平角的定义是解题的关键．