2020-2021学年第十四章 一次函数综合与测试课时练习

这是一份2020-2021学年第十四章 一次函数综合与测试课时练习，共27页。试卷主要包含了已知点，一次函数的一般形式是等内容，欢迎下载使用。
京改版八年级数学下册第十四章一次函数定向测试
考试时间：90分钟；命题人：数学教研组
考生注意：
1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟
2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上
3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。
第I卷（选择题 30分）
一、单选题（10小题，每小题3分，共计30分）
1、一次函数y＝－x＋2的图象与x轴，y轴分别交于A、B两点，以AB为腰，∠BAC＝90°，在第一象限作等腰Rt△ABC，则直线BC的解析式为（　　）

A． B． C． D．
2、一次函数y＝kx+b的图象如图所示，则下列说法错误的是（　　）

A．y随x的增大而减小
B．k＜0，b＜0
C．当x＞4时，y＜0
D．图象向下平移2个单位得y＝﹣x的图象
3、若点在第三象限，则点在（ ）．
A．第一象限 B．第二象限 C．第三象限 D．第四象限
4、若点A(x1，y1)和B(x2，y2) 都在一次函数y=(k)x+2(k为常数)的图像上，且当x1y2，则k的值可能是（ ）
A．k=0 B．k=1 C．k=2 D．k=3
5、在平面直角坐标系中，任意两点，，，．规定运算：①，；②；③当，且时，．
有下列三个命题：
（1）若，，则，；
（2）若，则；
（3）对任意点，，，均有成立．
其中正确命题的个数为（ ）
A．0个 B．1个 C．2个 D．3个
6、已知点(﹣4，y1)、(2，y2)都在直线y＝﹣x+b上，则y1和y2的大小关系是（ ）
A．y1＞y2 B．y1＝y2 C．y1＜y2 D．无法确定
7、一次函数的一般形式是(k，b是常数)（ ）
A．y=kx+b B．y=kx C．y=kx+b(k≠0) D．y=x
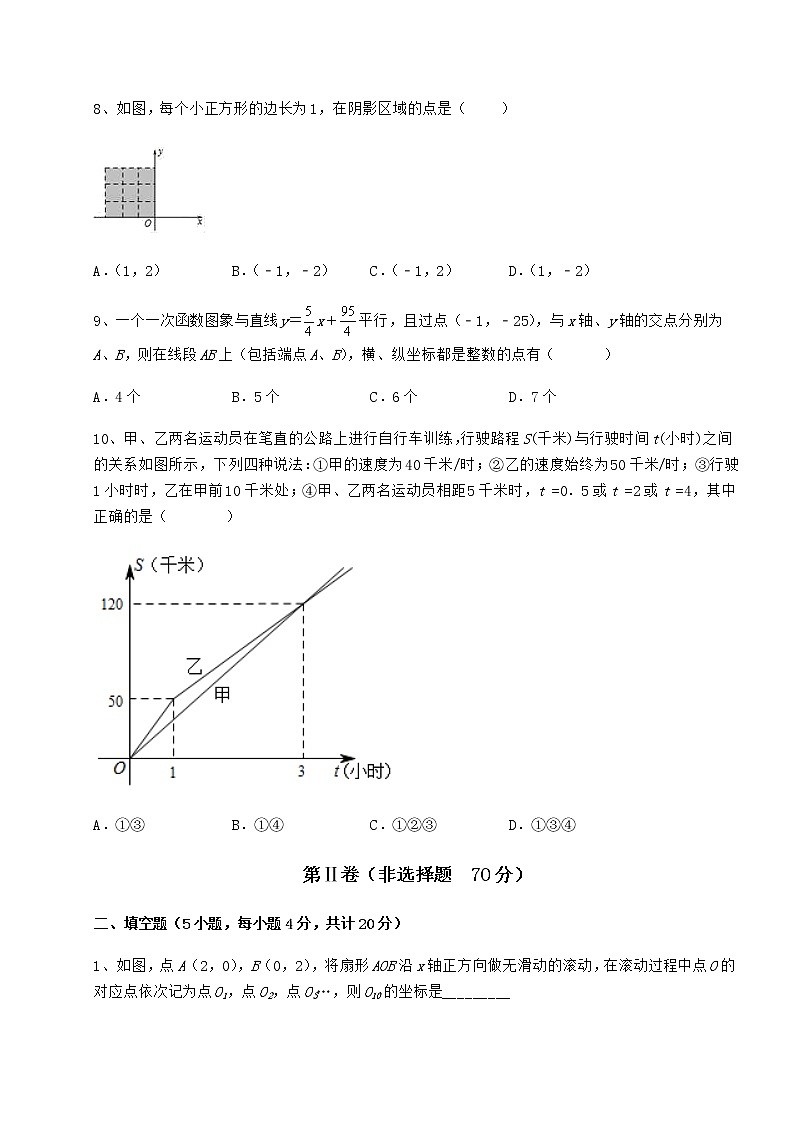
8、如图，每个小正方形的边长为1，在阴影区域的点是（   ）

A．（1，2）  B．（﹣1，﹣2） C．（﹣1，2） D．（1，﹣2）
9、一个一次函数图象与直线y＝x＋平行，且过点（﹣1，﹣25），与x轴、y轴的交点分别为A、B，则在线段AB上（包括端点A、B），横、纵坐标都是整数的点有（ ）
A．4个 B．5个 C．6个 D．7个
10、甲、乙两名运动员在笔直的公路上进行自行车训练，行驶路程S(千米)与行驶时间t(小时)之间的关系如图所示，下列四种说法：①甲的速度为40千米/时；②乙的速度始终为50千米/时；③行驶1小时时，乙在甲前10千米处；④甲、乙两名运动员相距5千米时，t =0．5或t =2或t =4，其中正确的是（ ）

A．①③ B．①④ C．①②③ D．①③④
第Ⅱ卷（非选择题 70分）
二、填空题（5小题，每小题4分，共计20分）
1、如图，点A（2，0），B（0，2），将扇形AOB沿x轴正方向做无滑动的滚动，在滚动过程中点O的对应点依次记为点O1，点O2，点O3…，则O10的坐标是_________

2、平面直角坐标系中，点P(3，－4)到x轴的距离是________．
3、学校“青春礼”活动当天，小明和妈妈以不同的速度匀速从家里前往学校，小明害怕集合迟到先出发2分钟，随后妈妈出发，妈妈出发几分钟后，两人相遇，相遇后两人以小明的速度匀速前进，行进2分钟后，通过与妈妈交谈，小明发现忘记穿校服，于是小明立即掉头以原速度的2倍跑回家中，妈妈速度减半，继续匀速赶往学校，小明到家后，花了3分钟换校服，换好校服后，小明再次从家里出发，并以返回时的速度跑回学校，最后小明和妈妈同时到达学校．小明和妈妈之间的距离y与小明出发时间x之间的关系如图所示．则小明家与学校之间的距离是_____米．

4、已知一次函数，且y的值随着x的值增大而减小，则m的取值范围是______．
5、如果点P（m+3，2m﹣4）在y轴上，那么m的值是 _____．
三、解答题（5小题，每小题10分，共计50分）
1、如图，长方形AOBC在直角坐标系中，点A在y轴上，点B在x轴上，已知点C的坐标是（8，4）．
（1）求对角线AB所在直线的函数关系式；
（2）对角线AB的垂直平分线MN交x轴于点M，连接AM，求线段AM的长；
（3）若点P是直线AB上的一个动点，当△PAM的面积与长方形OACB的面积相等时，求点P的坐标．

2、在平面直角坐标系中，直线y＝kx+4（k≠0）交x轴于点A（8，0），交y轴于点B．
（1）k的值是 　 　；
（2）点C是直线AB上的一个动点，点D和点E分别在x轴和y轴上．
①如图，点D的坐标为（6，0），点E的坐标为（0，1），若四边形OECD的面积是9，求点C的坐标；
②当CE平行于x轴，CD平行于y轴时，若四边形OECD的周长是10，请直接写出点C的坐标．

3、在平面直角坐标系中，的顶点，，的坐标分别为，，．与关于轴对称，点，，的对应点分别为，，．请在图中作出，并写出点，，的坐标．

4、在平面直角坐标系xOy中，一次函数y＝kx＋b（k≠0）的图象可由函数y＝x的图象平移得到，且经过点（﹣2，0）．
（1）求一次函数y＝kx＋b的表达式；
（2）将一次函数y＝kx＋b在x轴下方的图象沿x轴翻折到x轴上方，图象的其余部分不变，得到一个新图象（如图所示）．
①根据图象，当x＞﹣2时，y随x的增大而 　 　；
②请再写出两条该函数图象的性质．

5、已知一次函数的图像经过点A(－1，－2)，B(0，1)．
（1）求k、b的值；
（2）画出这个函数的图像；
（3）当x＞1时，y的取值范围是 ．


-参考答案-
一、单选题
1、D
【解析】
【分析】
由题意易得B的坐标是（0，2），A的坐标是（5，0），作CE⊥x轴于点E，则有∠ACE＝∠BAO，然后可得△ABO≌△CAE，进而可得C的坐标是（7，5），设直线BC的解析式是y＝kx＋b，最后利用待定系数法可求解．
【详解】
解：∵一次函数y＝－x＋2中，
令x＝0得：y＝2；令y＝0，解得x＝5，
∴B的坐标是（0，2），A的坐标是（5，0）．
若∠BAC＝90°，如图1，作CE⊥x轴于点E，
∵∠BAC＝90°，
∴∠OAB＋∠CAE＝90°，
又∵∠CAE＋∠ACE＝90°，
∴∠ACE＝∠BAO．
在△ABO与△CAE中，，
∴△ABO≌△CAE（AAS），
∴OB＝AE＝2，OA＝CE＝5，
∴OE＝OA＋AE＝2＋5＝7．
则C的坐标是（7，5）．
设直线BC的解析式是y＝kx＋b，
根据题意得：，解得，
∴直线BC的解析式是y＝x＋2．
故选：D．

【点睛】
本题主要考查一次函数与几何的综合，熟练掌握一次函数的图象与性质是解题的关键．
2、B
【解析】
【分析】
由一次函数的图象的走势结合一次函数与轴交于正半轴，可判断A，B，由图象可得：当x＞4时，函数图象在轴的下方，可判断C，先求解一次函数的解析式，再利用一次函数图象的平移可判断D，从而可得答案.
【详解】
解：一次函数y＝kx+b的图象从左往右下降，所以y随x的增大而减小，故A不符合题意；
一次函数y＝kx+b， y随x的增大而减小，与轴交于正半轴，所以 故B符合题意；
由图象可得：当x＞4时，函数图象在轴的下方，所以y＜0，故C不符合题意；
由函数图象经过
，解得：
所以一次函数的解析式为：
把向下平移2个单位长度得：，故D不符合题意；
故选B
【点睛】
本题考查的是一次函数的性质，一次函数的平移，利用待定系数法求解一次函数的解析式，掌握“一次函数的图象与性质”是解本题的关键.
3、A
【解析】
【分析】
根据第三象限点的横坐标与纵坐标都是负数，然后判断点Q所在的象限即可．
【详解】
∵点P（m，n）在第三象限，
∴m＜0，n＜0，
∴-m＞0，-n＞0，
∴点在第一象限．
故选：A．
【点睛】
本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
4、A
【解析】
【分析】
利用一次函数y随x的增大而减小，可得，即可求解．
【详解】
∵当x1y2
∴一次函数y=(k)x+2的y随x的增大而减小
∴
∴
∴k的值可能是0
故选：A．
【点睛】
本题考查了一次函数图象上点的坐标特征，解题关键是利用一次函数图象上点的坐标特征，求出．
5、D
【解析】
【分析】
根据新的运算定义分别判断每个命题后即可确定正确的选项．
【详解】
解：（1）A⊕B=（1+2，2-1）=（3，1），A⊗B=1×2+2×（-1）=0，
∴①正确；
（2）设C（x3，y3），A⊕B=（x1+x2，y1+y2），B⊕C=（x2+x3，y2+y3），
∵A⊕B=B⊕C，
∴x1+x2=x2+x3，y1+y2=y2+y3，
∴x1=x3，y1=y3，
∴A=C，
∴②正确．
（3）∵（A⊕B）⊕C=（x1+x2+x3，y1+y2+y3），A⊕（B⊕C）=（x1+x2+x3，y1+y2+y3），
∴（A⊕B）⊕C=A⊕（B⊕C），
∴③正确．
正确的有3个，
故选：D．
【点睛】
本题考查了命题与定理，解题时注意：判断一件事情的语句，叫做命题．有些命题的正确性是用推理证实的，这样的真命题叫做定理．
6、A
【解析】
【分析】
由题意直接根据一次函数的性质进行分析即可得到结论．
【详解】
解：∵直线y＝﹣x+b中，k＝﹣＜0，
∴y将随x的增大而减小．
∵﹣4＜2，
∴y1＞y2．
故选：A．
【点睛】
本题考查一次函数的图象性质，注意掌握对于一次函数y=kx+b（k≠0），当k＞0，y随x增大而增大；当k＜0时，y将随x的增大而减小．
7、C
【解析】
【分析】
根据一次函数的概念填写即可．
【详解】
解：把形如y=kx+b((k，b是常数，k≠0)的函数，叫做一次函数，
故选：C．
【点睛】
本题考查了一次函数的概念，做题的关键是注意k≠0．
8、C
【解析】
【分析】
根据平面直角坐标系中点的坐标的表示方法求解即可．
【详解】
解：图中阴影区域是在第二象限，
A.（1，2）位于第一象限，故不在阴影区域内，不符合题意；
B.（-1，-2）位于第三象限，故不在阴影区域内，不符合题意；
C.（﹣1，2）位于第二象限，其横纵坐标的绝对值不超过3，故在阴影区域内，符合题意；
D. （1，-2）位于第四象限，故不在阴影区域内，不符合题意．
故选：C．
【点睛】
此题考查了平面直角坐标系中四个象限中点的坐标特点，解题的关键是熟练掌握平面直角坐标系中四个象限中点的坐标特点：第一象限横坐标为正，纵坐标为正；第二象限横坐标为负，纵坐标为正；第三象限横坐标为负，纵坐标为负；第四象限横坐标为正，纵坐标为负．
9、A
【解析】
【分析】
由题意可得：求出符合条件的直线为5x﹣4y﹣75＝0，即可求出此直线与与x轴、y轴的交点分别为A（15，0）、B（0，﹣），再设出在直线AB上并且横、纵坐标都是整数的点的坐标，进而结合题意得到不等式求出N的范围，即可得到N的取值得到答案．
【详解】
解：设直线AB的解析式为y＝kx＋b，
∵一次函数图象与直线y＝x＋平行，
∴k＝，
又∵所求直线过点（﹣1，﹣25），
∴﹣25＝×（﹣1）＋b，
解得b＝﹣，
∴直线AB为y＝x﹣，
∴此直线与与x轴、y轴的交点分别为A（15，0）、B（0，﹣），
设在直线AB上并且横、纵坐标都是整数的点的横坐标是x＝﹣1＋4N，纵坐标是y＝﹣25＋5N，（N是整数）．
因为在线段AB上这样的点应满足0≤x＝﹣1＋4N≤15，且﹣＜y＝﹣25＋5N≤0，
解得：≤N≤4，
所以N＝1，2，3，4共4个，
故选：A．
【点睛】
本题考查一次函数图象上点的坐标特征，根据题意写出x和y的表示形式是解题的关键．
10、D
【解析】
【分析】
分析图像上每一段表示的实际意义，再根据行程问题计算即可．
【详解】
①甲的速度为，故正确；
②时，已的速度为，后，乙的速度为，故错误；
③行驶1小时时，甲走了40千米，乙走了50千米，乙在甲前10千米处，故正确；
④由①②③得：甲的函数表达式为：，
已的函数表达为：时，，时，，
时，甲、乙两名运动员相距，
时，甲、乙两名运动员相距，
时，甲、乙两名运动员相距为，故正确．
故选：D．
【点睛】
本题为一次函数应用题，此类问题主要通过图象计算速度，即分析每一段表示的实际意义进而求解．
二、填空题
1、（，2）
【解析】
【分析】
先求出的长度，然后分别求出点的坐标为（2，2），点的坐标为（，2），点的坐标为（，0），即可得到观察图形可知，O点坐标变化三次后回到x轴正半轴，每个回到x轴横坐标增加，由此求解即可．
【详解】
解：∵A（2，0），B（0，2），
∴OA=BA=2，∠AOB=90°，
∴的长度，
∵将扇形AOB沿x轴正方形做无滑动的滚动，
∴,，
∴点的坐标为（2，2），
∴点的坐标为（，2），
∴点的坐标为（，0），
∴观察图形可知，O点坐标变化三次后回到x轴正半轴，每个回到x轴横坐标增加，
∵10÷3=3余3，
∴点的坐标为（，2），即（，2），
故答案为：（，2）．
【点睛】
本题主要考查了点的坐标规律探索，求弧长，解题的关键在于能够根据题意找到规律求解．
2、4
【解析】
【分析】
根据点的坐标表示方法得到点P(3，﹣4)到x轴的距离是纵坐标的绝对值即|﹣4|，然后去绝对值即可．
【详解】
解：点P(3，-4)到x轴的距离为|﹣4|=4．
故答案为：4．
【点睛】
此题主要考查了点到坐标上的距离，正确掌握点的坐标性质是解题关键．
3、1760
【解析】
【分析】
根据函数图象可知，小明出发2分钟后走了160米，据此可得小明原来的速度，进而得出小明回时的速度．
【详解】
解：小明离家2分钟走了160米，
∴小明初始速度为160÷2＝80米/分；
小明返回家速度为80×2＝160米/分，妈妈继续行进速度80÷2＝40米/分；
小明在家换衣服3分钟时间，妈妈走了40×3＝120米，
设小明换好衣服离开家到与妈妈同时到达学校的时间为t分，
则有160t＝1200+120+40t，
∴t＝11，
∴小明离家距离为11×160＝1760米．
故答案为：1760米．
【点睛】
本题主要是考查了从函数图像获取信息，解题的关键是根据题意正确分析出函数图像中的数据．
4、m＜
【解析】
【分析】
利用一次函数的性质可得出关于m的一元一次不等式，解之即可得出m的取值h^$范围．
【详解】
解：∵一次函数的y值随着x值的增大而减小，
∴3m+1＜0，
∴m＜．
故答案为：m＜．
【点睛】
本题考查了一次函数的性质，牢记“k＞0，y随x的增大而增大；k＜0，y随x的增大而减小”是解题的关键．
5、-3
【解析】
【分析】
点P在y轴上则该点横坐标为0，可解得m的值．
【详解】
解：在y轴上，
∴m+3=0，
解得m=-3．
故答案为：-3．
【点睛】
本题主要考查了点的坐标，解决本题的关键是掌握好坐标轴上的点的坐标的特征，y轴上的点的横坐标为0．
三、解答题
1、（1）；（2）5；（3）点P的坐标为（，－445）或（－，845）
【解析】
【分析】
（1）由坐标系中点的意义结合图形可得出A、B点的坐标，设出对角线AB所在直线的函数关系式，由待定系数法即可求得结论；
（2）由勾股定理求出AB的长，再结合线段垂直平分线的性质，可得AM＝BM，OM＝OB−BM，再次利用勾股定理得出AM的长；
（3）（方法一）先求出直线AM的解析式，设出P点坐标，由点到直线的距离求出AM边上的高h，再结合三角形面积公式与长方形面积公式即可求出P点坐标；
（方法二）由△PAM的面积与长方形OACB的面积相等可得出S△PAM的值，设点P的坐标为（x，−x＋4），分点P在AM的右侧及左侧两种情况，找出关于x的一元一次方程，解之即可得出点P的坐标，此题得解．
【详解】
解：（1）∵四边形AOBC为长方形，且点C的坐标是（8，4），
∴AO＝CB＝4，OB＝AC＝8，
∴A点坐标为（0，4），B点坐标为（8，0）．
设对角线AB所在直线的函数关系式为y＝kx＋b，
则有4=b0=8k+b，解得：，
∴对角线AB所在直线的函数关系式为y＝－x＋4．
（2）∵∠AOB＝90°，
∴勾股定理得：AB＝AO2+OB2＝45，
∵MN垂直平分AB，
∴BN＝AN＝AB＝25．
∵MN为线段AB的垂直平分线，
∴AM＝BM
设AM＝a，则BM＝a，OM＝8－a，
由勾股定理得，a2＝42＋（8－a）2，
解得a＝5，即AM＝5．
（3）（方法一）∵OM＝3，
∴点M坐标为（3，0）．
又∵点A坐标为（0，4），
∴直线AM的解析式为y＝－x＋4．
∵点P在直线AB：y＝－x＋4上，
∴设P点坐标为（m，－m＋4），
点P到直线AM：x＋y－4＝0的距离h＝43m-12m+4-4432+12＝m2．
△PAM的面积S△PAM＝AM•h＝|m|＝SOABC＝AO•OB＝32，
解得m＝± ，
故点P的坐标为（，－445）或（－，845）．

（方法二）∵S长方形OACB＝8×4＝32，
∴S△PAM＝32．
设点P的坐标为（x，－x＋4）．
当点P在AM右侧时，S△PAM＝MB•（yA－yP）＝×5×（4＋x－4）＝32，
解得：x＝，
∴点P的坐标为（，－445）；
当点P在AM左侧时，S△PAM＝S△PMB－S△ABM＝MB•yP－10＝×5（－x＋4）－10＝32，
解得：x＝－，
∴点P的坐标为（－，845）．
综上所述，点P的坐标为（，－445）或（－，845）．
【点睛】
本题考查了坐标系中点的意、勾股定理、点到直线的距离、三角形和长方形的面积公式，解题的关键：（1）根据坐标系中点的意义，找到A、B点的坐标；（2）由线段垂直平分线的性质和勾股定理找出BM的长度；（3）（方法一）结合点到直线的距离、三角形和长方形的面积公式找到关于m的一元一次方程；（方法二）利用分割图形求面积法找出关于x的一元一次方程．本题属于中等题，难度不大，运算量不小，这里尤其要注意点P有两个．
2、（1）；（2）①；②或.
【解析】
【分析】
（1）把A（8，0）的坐标代入函数解析式即可；
（2）①由四边形,则在线段上时，如图，利用四边形OECD的面积是9，再列方程解题即可；②分三种情况讨论，如图，当在线段上时， 当在的延长线上时，当在的延长线时，设再利用四边形OECD的周长是10，列方程求解即可.
【详解】
解：（1） 直线y＝kx+4（k≠0）交x轴于点A（8，0），
解得：
故答案为：
（2）①由（1）得：
令 则 即

点D的坐标为（6，0），点E的坐标为（0，1），

设
由四边形OECD的面积是9，则在线段上，

解得： 则

②当CE平行于x轴，CD平行于y轴时，
轴，轴，
如图，当在线段上时，设

则
四边形OECD的周长是10，

解得： 则

当在的延长线上时，

同理可得：

解得： 则

当在的延长线时，如图，

四边形的周长大于,故不符合题意，舍去，
综上：或.
【点睛】
本题考查的是一次函数的性质，坐标与图形，掌握“利用周长与面积列方程”是解本题的关键.
3、作图见解析，点A' （-3 ， 2 ），点B' （-1 ， -2 ），点C' （-4 ， -3 ）
【解析】
【分析】
分别作出A，B，C的对应点，，即可．
【详解】
解： 如图所示．
点A'（-3，2 ），点B'（-1，-2 ），点C'（-4，-3 ）．

【点睛】
本题考查了作图-轴对称变换，直角坐标系中表示点的坐标，熟知关于y轴对称的点的坐标特点是解答此题的关键．
4、（1）y＝x+2；（2）①增大；②函数有最小值0；函数图象关于直线x＝﹣2对称
【解析】
【分析】
（1）先根据直线平移时k的值不变得出k＝1，再将点（﹣2，0）代入y＝x+b，求出b的值，即可得到一次函数的解析式；
（2）观察图象即可求得．
【详解】
解：（1）∵一次函数y＝kx+b的图象由函数y＝x的图象平移得到，
∴k＝1，
又∵一次函数y＝x+b的图象过点（﹣2，0），
∴﹣2+b＝0．
∴b＝2，
∴这个一次函数的表达式为y＝x+2；
（2）将一次函数y＝kx+b在x轴下方的图象沿x轴翻折到x轴上方，图象的其余部分不变，得到一个新图象（如图所示）．

①根据图象，当x＞﹣2时，y随x的增大而增大，
故答案是：增大；
②函数有最小值0；函数图象关于直线x＝﹣2对称．
【点睛】
本题考查了一次函数图象与几何变换，一次函数与系数的关系，数形结合是解题的关键．
5、（1）；（2）见详解；（3）
【解析】
【分析】
（1）由待定系数法进行计算，即可得到答案；
（2）由两点画图法，即可画出一次函数的图像；
（3）结合一次函数的性质，即可得到答案．
【详解】
解：（1）∵一次函数的图像经过点A(－1，－2)，B(0，1)
∴，
∴；
（2）由（1）可知，一次函数为经过点A(－1，－2)，B(0，1)，如图：

（3）当时，则，
由图像可知，y随x增大而增大，
∴当x＞1时，y的取值范围是；
故答案为：．
【点睛】
本题考查了待定系数法求一次函数的解析式，画函数图像，解题的关键是正确的求出一次函数的解析式．