初中数学北京课改版八年级下册第十六章 一元二次方程综合与测试课时作业

这是一份初中数学北京课改版八年级下册第十六章 一元二次方程综合与测试课时作业，共21页。试卷主要包含了方程x2﹣x＝0的解是等内容，欢迎下载使用。
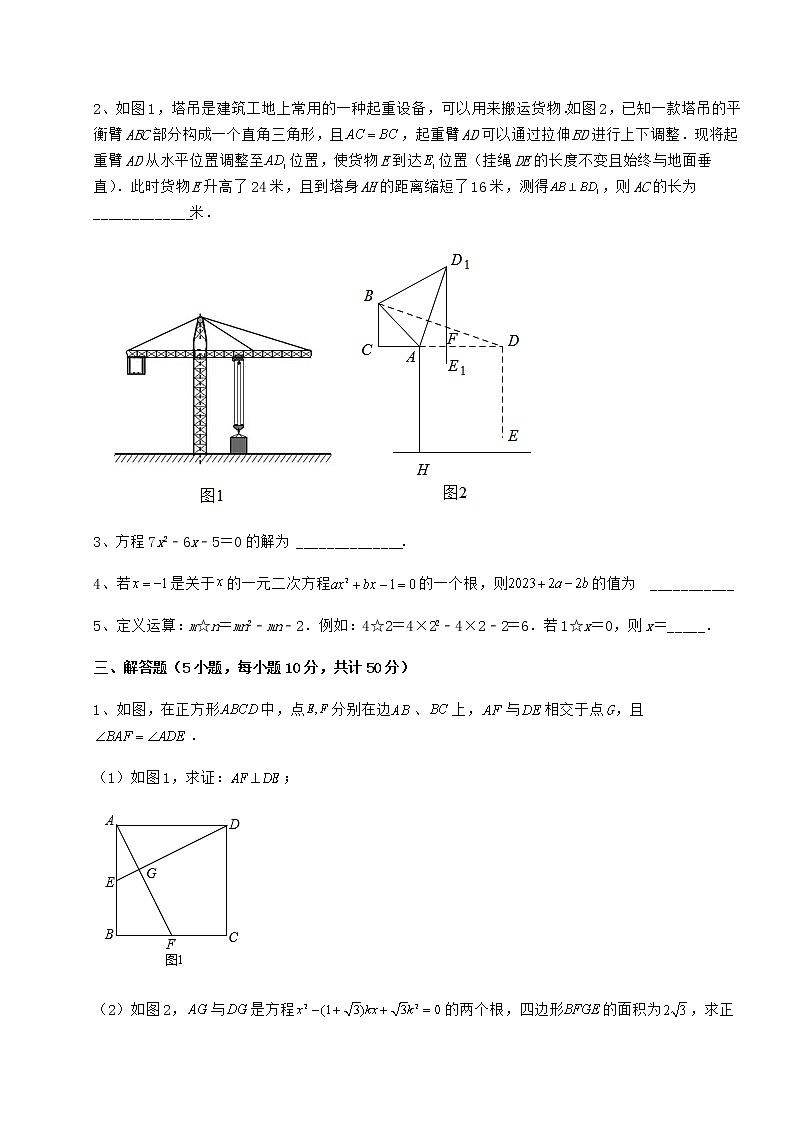
京改版八年级数学下册第十六章一元二次方程同步训练 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、若关于x的一元二次方程的一根为1，则k的值为（    ） ．A．1 B． C． D．02、为落实教育优先发展，南充市财政一般公共预算2019年教育经费投入93.15亿元，2021年教育经费投入99.45亿元，设南充市财政一般公共预算教育经费投入年平均增长率为x，则可列方程为（    ）A． B．C． D．3、一元二次方程根的情况是（    ）A．有两个不相等的实数根 B．有两个相等的实数根C．没有实数根 D．无法判断4、下表是用计算器探索函数y＝2x2﹣2x﹣10所得的数值，则方程2x2﹣2x﹣10＝0的一个近似解为（    ） x﹣2.1﹣2.2﹣2.3﹣2.4y﹣1.39﹣0.76﹣0.110.56A．x≈﹣2.15 B．x≈﹣2.21 C．x≈﹣2.32 D．x≈﹣2.415、用配方法解方程x2＋4x＝1，变形后结果正确的是（    ）A．(x＋2)2＝5 B．(x＋2)2＝2 C．(x－2)2＝5 D．(x－2)2＝26、一个三角形两边的长分别等于一元二次方程的两个实数根，则这个三角形的第三条边不可能为（    ）A．7 B．11 C．15 D．197、若关于x的方程kx2﹣4x﹣2＝0有实数根，则实数k的取值范围是（　　）A．k≥2 B．k≥﹣2 C．k＞﹣2且k≠0 D．k≥﹣2且k≠08、某种芯片实现国产化后，经过两次降价，每块芯片单价由128元降为88元.若两次降价的百分率相同，设每次降价的百分率为x，根据题意，可列方程A．128（1 - x2）= 88 B．88（1 + x)2 = 128C．128（1 - 2x）= 88 D．128（1 - x)2 = 889、方程x2﹣x＝0的解是（　　）A．x＝0 B．x＝1 C．x1＝0，x2＝﹣1 D．x1＝0，x2＝110、已知一元二次方程ax2+bx+c=3有一个根为x=－2，且a+b+c=3，则一元二次方程ax2－bx+c=3的两根分别为（   ）A．x1=0，x2=－3 B．x1=－1，x2=－4C．x1=0，x2=3， D．x1=2，x2=－1第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、已知（x+3）（x﹣2）+m＝x2+x，则一元二次方程x2+x﹣m＝0的根是 _____．2、如图1，塔吊是建筑工地上常用的一种起重设备，可以用来搬运货物．如图2，已知一款塔吊的平衡臂ABC部分构成一个直角三角形，且，起重臂AD可以通过拉伸BD进行上下调整．现将起重臂AD从水平位置调整至位置，使货物E到达位置（挂绳DE的长度不变且始终与地面垂直）．此时货物E升高了24米，且到塔身AH的距离缩短了16米，测得，则AC的长为_____________米．3、方程7x2﹣6x﹣5＝0的解为 ______________．4、若是关于的一元二次方程的一个根，则的值为  ___________5、定义运算：m☆n＝mn2﹣mn﹣2．例如：4☆2＝4×22﹣4×2﹣2＝6．若1☆x＝0，则x＝_____．三、解答题（5小题，每小题10分，共计50分）1、如图，在正方形中，点分别在边、上，与相交于点G，且．（1）如图1，求证：；（2）如图2，与是方程的两个根，四边形的面积为，求正方形的面积．（3）在第（2）题的条件下，如图3，延长BC至点N，使得CN=3，连接GN交CD于点M，直接写出线段的值．2、为了让我们的小朋友们有更好的学习环境，我校2020年投资110万元改造硬件设施，计划以后每年以相同的增长率进行投资，到2022年投资额将达到185.9万元．（1）求我校改造硬件设施投资额的年平均增长率；（2）从2020年到2022年，这三年我校将总共投资多少万元？3、解方程：（1）（x﹣5）2＝（2﹣3x）2；（2）x2﹣10x+16＝0；（3）2x2﹣x﹣2＝0．4、某市为鼓励居民节约用水，对居民用水实行阶梯收费，每户居民用水量每月不超过a吨时，每吨按0.3a元缴纳水费；每月超过a吨时，超过部分每吨按0.4a元缴纳水费．（1）若a＝12，某户居民3月份用水量为22吨，则该用户应缴纳水费多少元？（2）若如表是某户居民4月份和5月份的用水量和缴费情况：月份用水量（吨）交水费总金额（元）4186252486根据上表数据，求规定用水量a的值5、已知函数y1＝x＋1和y2＝x2＋3x＋c（c为常数）.（1）若两个函数图像只有一个公共点，求c的值；（2）点A在函数y1的图像上，点B在函数y2的图像上，A，B两点的横坐标都为m．若A，B两点的距离为3，直接写出满足条件的m值的个数及其对应的c的取值范围． -参考答案-一、单选题1、B【分析】把方程的根代入方程可以求出k的值．【详解】解：把1代入方程有：
1+2k+1=0，
解得：k=-1，
故选：B．【点睛】本题考查的是一元二次方程的解，正确理解题意是解题的关键．2、A【分析】根据题意可直接进行求解．【详解】解：由题意可列方程为；故选A．【点睛】本题主要考查一元二次方程的应用，熟练掌握增长率问题是解题的关键．3、A【分析】计算出判别式的值，根据判别式的值即可判断方程的根的情况．【详解】∵，，，∴，∴方程有有两个不相等的实数根．故选：A【点睛】本题考查了一元二次方程根的判别式，根据判别式的值的情况可以判断方程有无实数根．4、C【分析】根据表可得，方程2x2﹣2x﹣10＝0的一个解应在﹣2.3与﹣2.4之间，再由y的值可得，它的根近似的看作是﹣2.3．【详解】∵当x＝﹣2.3时，y＝﹣0.11，当x＝﹣2.4时，y＝0.56，则方程的根﹣2.3＜x＜﹣2.4，∵|﹣0.11|＜|0.56|，∴方程2x2﹣2x﹣10＝0的一个近似解为x≈﹣2.32．故选：C．【点睛】本题考查了用图象法求一元二次方程的近似根，解题的关键是看y值的变化．5、A【分析】方程的两边同时加上一次项系数一半的平方即可，进而即求得答案．【详解】解：x2＋4x＝1即故选A【点睛】本题考查了配方法解一元二次方程，掌握配方法是解题的关键．6、D【分析】先根据一元二次方程的解法得到这个三角形的两边长，然后再利用三角形三边关系可排除选项．【详解】解：，解得：，∴这个三角形的两边的长为6和11，∴第三边长x的范围为5＜x＜17；故选D．【点睛】本题主要考查一元二次方程的解法及三角形三边关系，熟练掌握一元二次方程的解法及三角形三边关系是解题的关键．7、B【分析】根据当时，方程是一元一次方程有实数根，当时，根据一元二次方程的定义和根的判别式的意义得到k≠0且Δ=（-4）2-4 k×（-2）≥0，然后求出两不等式组的公共部分，两种情况合并即可．【详解】解：根据题意得：①当时，方程是一元一次方程，此时﹣4x﹣2＝0，方程有实数解；②当时，此方程是一元二次方程，可得k≠0且Δ=（-4）2-4 k×（-2）≥0，解得k≥-2且k≠0．综上，当时，关于x的方程kx2﹣4x﹣2＝0有实数根，故选：B．【点睛】本题考查了根的判别式：一元二次方程ax2+bx+c=0（a≠0）的根与Δ=b2-4ac有如下关系：当Δ＞0时，方程有两个不相等的实数根；当Δ=0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根．上面的结论反过来也成立．8、D【分析】根据该药品的原售价及经过两次降价后的价格，即可得出关于x的一元二次方程，此题得解．【详解】解：依题意得：128（1-x）2=88．
故选：D．【点睛】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．9、D【分析】因式分解后求解即可.【详解】x2﹣x＝0，x（x-1）=0，x=0，或x-1=0，解得x1＝0，x2＝1，故选：D【点睛】此题考查因式分解法解一元二次方程，因式分解法解一元二次方程的一般步骤：①移项，使方程的右边化为零；②将方程的左边分解为两个一次因式的乘积；③令每个因式分别为零，得到两个一元一次方程；④解这两个一元一次方程，它们的解就都是原方程的解．10、D【分析】首先根据a+b+c=3可得一元二次方程ax2+bx+c=3的一个根为，然后根据根与系数的关系可得，，然后代入一元二次方程ax2－bx+c=3中即可求解．【详解】解：∵一元二次方程ax2+bx+c=3有一个根为x=－2，且a+b+c=3，∴一元二次方程ax2+bx+c=3有一个根为1，∴一元二次方程ax2+bx+c=3化成一般形式为ax2+bx+c-3＝0，∴，，∵ax2－bx+c=3化成一般形式为ax2-bx+c-3＝0，即，∴，∴，∴或，解得：．故选：D．【点睛】此题考查了一元二次方程的解，因式分解法解一元二次方程，一元二次方程根与系数的关系，解题的关键是熟练掌握一元二次方程根与系数的关系．二、填空题1、或.【分析】由题意将（x+3）（x﹣2）+m＝x2+x变形为，进而即可求得一元二次方程x2+x﹣m＝0的根.【详解】解：∵（x+3）（x﹣2）+m＝x2+x，∴， ∵x2+x﹣m＝0，∴，解得：或.故答案为：或.【点睛】本题考查求一元二次方程的根，注意将（x+3）（x﹣2）+m＝x2+x变形为是解题的关键.2、7【分析】过点B作于点M，由题意易得，则有四边形是矩形，设，则，然后根据勾股定理可得AF的长，进而问他可求解．【详解】解：过点B作于点M，如图所示：由题意得：，∴四边形是矩形，∴，设，则，在中，由勾股定理得：，解得：，∴，设，∴，∴，在中，，在中，，∴，整理得：，解得：；故答案为7．【点睛】本题主要考查勾股定理、矩形的性质与判定及一元二次方程的解法，熟练掌握勾股定理、矩形的性质与判定及一元二次方程的解法是解题的关键．3、【分析】找出a，b，c的值，代入求根公式即可求出解．【详解】解：7x2﹣6x﹣5＝0∵a＝7，b＝﹣6，c＝﹣5，∵△＝36﹣4×7×（﹣5）＝176＞0，∴ ，∴x1＝，x2＝．【点睛】本题考查一元二次方程的解法，常用的解法有：直接开方法，配方法，公式法，因式分解法，做题的关键是根据题目选择合适的方法．4、2025【分析】把代入方程即可求得的值，然后将其整体代入所求的代数式求解即可.【详解】把代入方程得：，.故答案为：2025.【点睛】本题主要考查一元二次方程的解及代数式求值，解题关键是熟练掌握计算法则.5、2或﹣1【分析】根据题目中的新定于，可以将1☆x＝0转化为一元二次方程，然后求解即可．【详解】解：∵m☆n＝mn2﹣mn﹣2，1☆x＝0，∴x2﹣x﹣2＝0，∴（x﹣2）（x+1）＝0，解得x1＝2，x2＝﹣1，故答案为：2或﹣1．【点睛】本题考查了一元二次方程的应用，解题的关键是列出相应的方程，会用新定义解答问题．三、解答题1、（1）见解析；（2）16；（3）【分析】（1）由正方形ABCD得，由得，从而得出即可得证；（2）由ASA证明，从而得出，设，，则，即，由根与系数的关系求出k，即可得出；（3）过点G作PQ⊥AD于点P，交BC于Q，则GQ⊥BC，由（2）可知，，，，由等面积法求出PG，由勾股定理求出AP，故可得QG、QN，由勾股定理即可求出答案．【详解】（1）∵四边形ABCD是正方形，∴，∵，∴，∴，∴；（2）∵四边形ABCD是正方形，∴，在与中，，，∴，设，，则，即，∵与是方程的两个根，∴，∴，解得：，，∴，∴，∴一元二次方程为，；（3）如图，过点G作PQ⊥AD于点P，交BC于Q，则GQ⊥BC，由（2）可知，，，，，，则，，，∴，．【点睛】本题考查正方形的性质，全等三角形的判定与性质，一元二次方程根与系数的关系以及勾股定理，掌握知识点间的相互应用是解题的关键．2、（1）我校改造硬件设施投资额的年平均增长率为30%；（2）从2020年到2022年，这三年我校将总共投资438.9万元【分析】（1）设我校改造硬件设施投资额的年平均增长率为x，利用2022年投资额＝2020年投资额×（1+年平均增长率）2，即可得出关于x的一元二次方程，解之取其正值即可得出结论；（2）利用这三年我校总共投资的金额＝2020年投资额+2020年投资额×（1+年平均增长率）+2022年投资额，即可求出结论．【详解】解：（1）设我校改造硬件设施投资额的年平均增长率为x，依题意得：110（1+x）2＝185.9，解得：x1＝0.3＝30%，x2＝﹣2.3（不合题意，舍去）．答：我校改造硬件设施投资额的年平均增长率为30%．（2）110+110×（1+30%）+185.9＝110+143+185.9＝438.9（万元）．答：从2020年到2022年，这三年我校将总共投资438.9万元【点睛】本题考查了一元二次方程的应用以及有理数的混合运算，解题的关键是：（1）找准等量关系，正确列出一元二次方程；（2）根据各数量之间的关系，列式计算．3、（1）x1＝，x2＝﹣；（2）x1＝2，x2＝8；（3）x1＝，x2＝﹣．【分析】（1）直接利用因式分解的方法解一元二次方程即可；（2）直接利用因式分解的方法解一元二次方程即可；（3）直接利用因式分解的方法解一元二次方程即可．【详解】解：（1）∵（x﹣5）2＝（2﹣3x）2，∴，∴，∴解得：x1＝，x2＝；（2）∵x2﹣10x+16＝0，∴（x﹣2）（x﹣8）＝0，∴x﹣2＝0或x﹣8＝0，解得x1＝2，x2＝8；（3）∵，∴，∴，∴，．【点睛】本题主要考查了解一元二次方程 ，解题的关键在于能够熟练掌握解一元二次方程的方法．4、（1） ；（2）10【分析】（1）根据题意得：该用户3月份用水量超过a吨，然后根据“用水量每月不超过a吨时，每吨按0.3a元缴纳水费；每月超过a吨时，超过部分每吨按0.4a元缴纳水费”，即可求解；（2）若 ，可得 ，从而得到 ，再由“用水量每月不超过a吨时，每吨按0.3a元缴纳水费；每月超过a吨时，超过部分每吨按0.4a元缴纳水费”，列出方程，即可求解．【详解】解：（1）根据题意得：该用户3月份用水量超过a吨， 元；（2）若 ，有 ，解得： ，即 ，不合题意，舍去，∴ ，根据题意得： ，解得： （舍去），答：规定用水量a的值为10吨．【点睛】本题主要考查了一元二次方程的应用，明确题意，准确得到等量关系是解题的关键．5、（1）c＝2；（2）当c＞5时，m有0个；当c＝5时，m有1个；当－1＜c＜5时，m有2个；当c＝－1时，m有3个；当c＜－1时，m有4个【分析】（1）只需求出y1=y2时对应一元二次方程有两个相等的实数根的c值即可；（2）根据题意，AB=｜m2＋2m＋c－1｜=3，分m2＋2m＋c－1＞0和m2＋2m＋c－1＜0两种情况，利用一元二次方程根的判别式与根的关系求解即可．【详解】解：（1）根据题意，若两个函数图像只有一个公共点，则方程x2＋3x＋c＝x＋1有两个相等的实数根，∴△=b2－4ac＝22－4(c－1)＝0，∴c＝2；（2）由题意，A（m，m+1），B（m，m2＋3m＋c）∴AB=｜m2＋3m＋c－m－1｜=｜m2＋2m＋c－1｜=3，①当m2＋2m＋c－1＞0时，m2＋2m＋c－1=3，即m2＋2m＋c－4=0，△=22－4（c－4）=20－4c，令△=20－4c=0，解得：c=5，∴当c＜5时，△＞0，方程有两个不相等的实数根，即m有2个；当c=5时，△=0，方程有两个相等的实数根，即m有1个；当c＞5时，△＜0，方程无实数根，即m有0个；②当m2＋2m＋c－1＜0时，m2＋2m＋c－1=－3，即m2＋2m＋c+2=0，△=22－4（c+2）=－4c－4，令△=－4c－4=0，解得：c=－1，∴当c＜－1时，△＞0，方程有两个不相等的实数根，即m有2个；当c=－1时，△=0，方程有两个相等的实数根，即m有1个；当c＞－1时，△＜0，方程无实数根，即m有0个；综上，当c＞5时，m有0个；当c＝5时，m有1个；当－1＜c＜5时，m有2个；当c＝－1时，m有3个；当c＜－1时，m有4个．【点睛】本题考查函数图象上点的坐标特征、一元二次方程根的判别式与根的关系、坐标与图形，解答的关键是熟练掌握一元二次方程根的判别式与根的关系：△＞0，方程有两个不相等的实数根，△=0，方程有两个相等的实数根，△＜0，方程无实数根．