数学九年级下册第24章 圆综合与测试达标测试

这是一份数学九年级下册第24章 圆综合与测试达标测试，共35页。试卷主要包含了已知⊙O的半径为4，，则点A在等内容，欢迎下载使用。
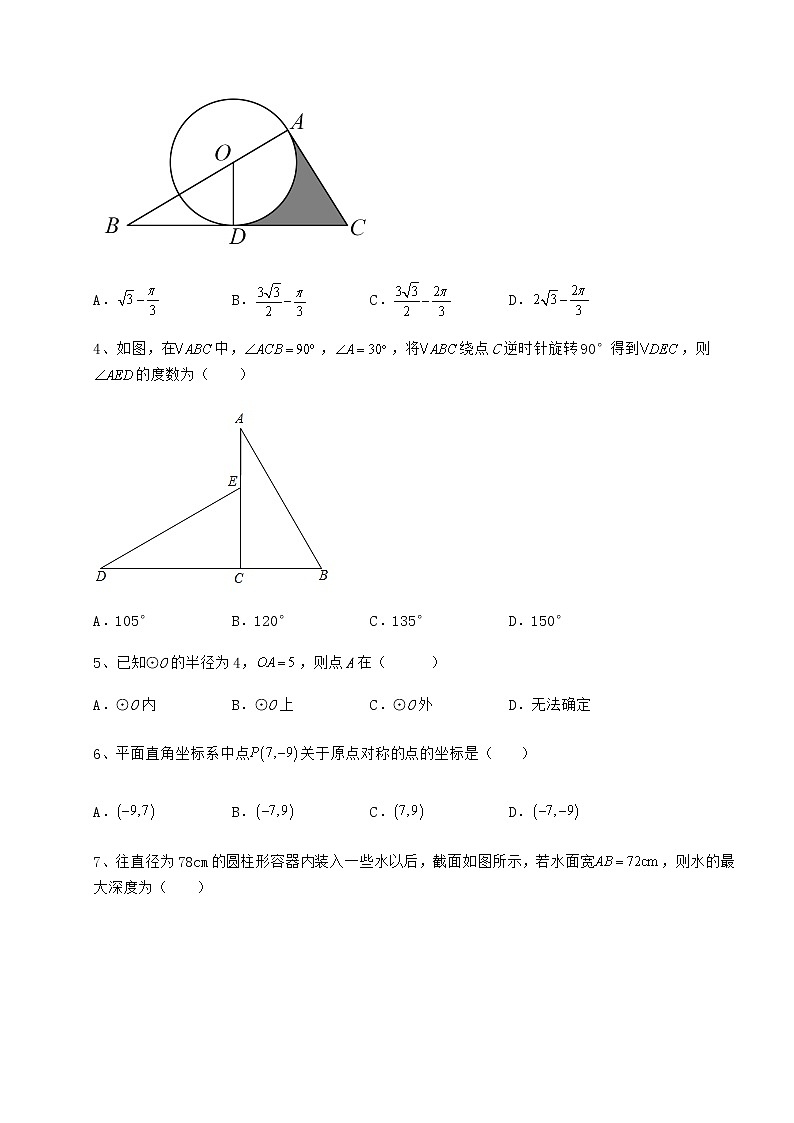
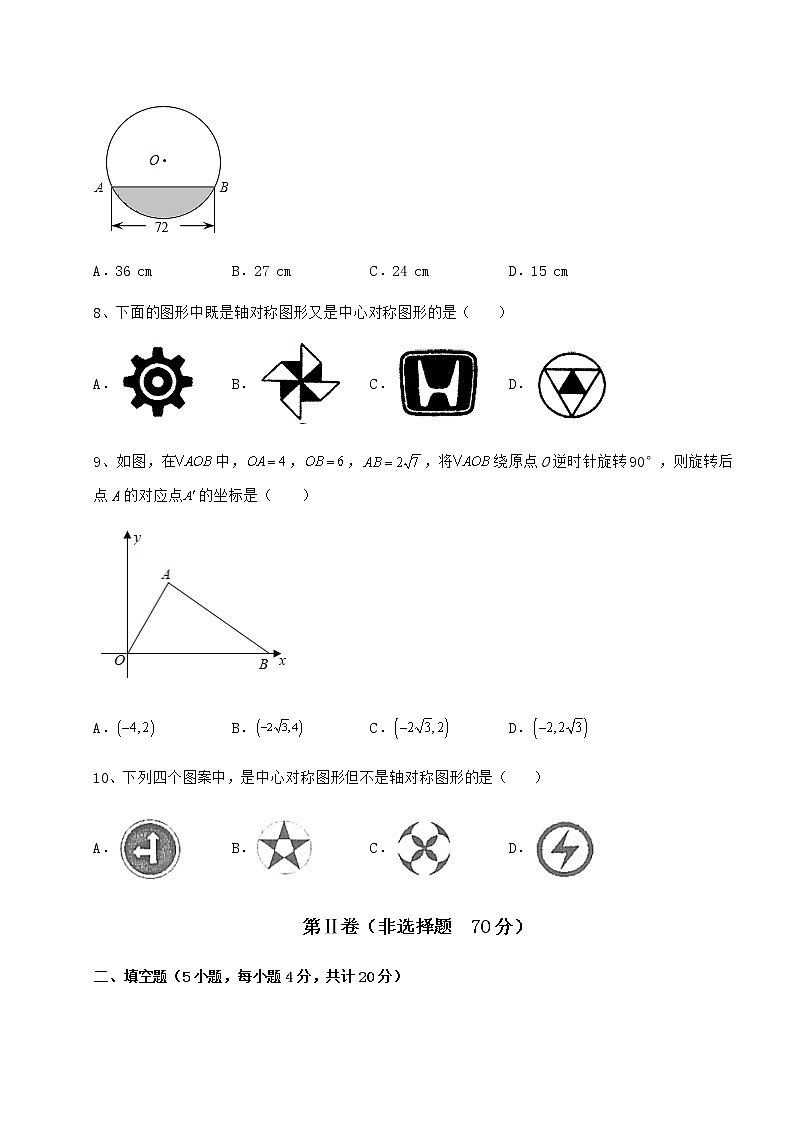
沪科版九年级数学下册第24章圆定向练习 考试时间：90分钟；命题人：数学教研组考生注意：1、本卷分第I卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分，考试时间90分钟2、答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置，如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带，不按以上要求作答的答案无效。第I卷（选择题  30分）一、单选题（10小题，每小题3分，共计30分）1、如图，AB是⊙O的直径，弦，，，则阴影部分图形的面积为（    ）A． B． C． D．2、点P(3，﹣2)关于原点O的对称点的坐标是（　　）A．(3，﹣2) B．(﹣3，2) C．(﹣3，﹣2) D．(2，3)3、如图，在Rt△ABC中，，，，以边上一点为圆心作，恰与边，分别相切于点，，则阴影部分的面积为（    ）A． B． C． D．4、如图，在中，，，将绕点C逆时针旋转90°得到，则的度数为（    ）A．105° B．120° C．135° D．150°5、已知⊙O的半径为4，，则点A在（      ）A．⊙O内 B．⊙O上 C．⊙O外 D．无法确定6、平面直角坐标系中点关于原点对称的点的坐标是（    ）A． B． C． D．7、往直径为78cm的圆柱形容器内装入一些水以后，截面如图所示，若水面宽，则水的最大深度为（    ）A．36 cm B．27 cm C．24 cm D．15 cm8、下面的图形中既是轴对称图形又是中心对称图形的是（    ）A． B． C． D．9、如图，在中，，，，将绕原点O逆时针旋转90°，则旋转后点A的对应点的坐标是（    ）A． B． C． D．10、下列四个图案中，是中心对称图形但不是轴对称图形的是（    ）A． B． C． D．第Ⅱ卷（非选择题  70分）二、填空题（5小题，每小题4分，共计20分）1、已知如图，AB=8，AC=4，∠BAC=60°，BC所在圆的圆心是点O，∠BOC=60°，分别在、线段AB和AC上选取点P、E、F，则PE+EF+FP的最小值为____________．2、把一个正六边形绕其中心旋转，至少旋转________度，可以与自身重合．3、如图，⊙O的半径为2，△ABC是⊙O的内接三角形，连接OB、OC，若弦BC的长度为，则∠BAC＝________度．4、如图，点D为边长是的等边△ABC边AB左侧一动点，不与点A，B重合的动点D在运动过程中始终保持∠ADB＝120°不变，则四边形ADBC的面积S的最大值是 ____．5、如图，在平面直角坐标系中，点N是直线上动点，M是上动点，若点C的坐标为，且与y轴相切，则长度的最小值为____________．三、解答题（5小题，每小题10分，共计50分）1、如图，正方形ABCD的顶点A、B在x轴的负半轴上，顶点CD在第二象限．将正方形ABCD绕点A按顺时针方向旋转，B、C、D的对应点分别为B1、C1、D1，且D1、C1、O三点在一条直线上．记点D1的坐标是（m，n），C1的坐标是（p，q）．（1）设∠DAD1＝30°，n＝2，求证：OD1的长度；（2）若∠DAD1＜90°，m，n满足m+n＝﹣4，p2+q2＝25，求p+q的值．2、如图1，在⊙O中，AC＝BD，且AC⊥BD，垂足为点E．（1）求∠ABD的度数；（2）图2，连接OA，当OA＝2，∠OAB＝15°，求BE的长度；（3）在（2）的条件下，求的长．3、如图，AB是⊙O的直径，点C是⊙O上一点，连接BC，半径OD弦BC．（1）求证：弧AD=弧CD；（2）连接AC、BD相交于点F，AC与OD相交于点E，连接CD，若⊙O的半径为5，BC=6，求CD和EF的长．4、对于平面直角坐标系xOy中的图形M和点P给出如下定义：Q为图形M上任意一点，若P，Q两点间距离的最大值和最小值都存在，且最大值是最小值的2倍，则称点P为图形M的“二分点”．已知点N（3，0），A（1，0），，．（1）①在点A，B，C中，线段ON的“二分点”是______；②点D（a，0），若点C为线段OD的“二分点”，求a的取值范围；（2）以点O为圆心，r为半径画圆，若线段AN上存在的“二分点”，直接写出r的取值范围．5、如图，⊙O的半径为10cm，弦AB垂直平分半径OC，垂足为点D．（1）弦AB的长为          ．（2）求劣弧的长． -参考答案-一、单选题1、D【分析】根据垂径定理求得CE=ED=；然后由圆周角定理知∠COE=60°．然后通过解直角三角形求得线段OC，然后证明△OCE≌△BDE，得到求出扇形COB面积，即可得出答案．【详解】解：设AB与CD交于点E，∵AB是⊙O的直径，弦CD⊥AB，CD=2，如图，∴CE=CD=，∠CEO=∠DEB=90°，∵∠CDB=30°，∴∠COB=2∠CDB=60°，∴∠OCE=30°，∴，∴，又∵，即∴，在△OCE和△BDE中，，∴△OCE≌△BDE（AAS），∴∴阴影部分的面积S=S扇形COB=，故选D．【点睛】本题考查了垂径定理、含30度角的直角三角形的性质，全等三角形的性质与判定，圆周角定理，扇形面积的计算等知识点，能知道阴影部分的面积=扇形COB的面积是解此题的关键．2、B【分析】根据“平面直角坐标系中任意一点P（x，y），关于原点的对称点是（﹣x，﹣y），即关于原点的对称点，横纵坐标都变成相反数”解答．【详解】解：点P（3，﹣2）关于原点O的对称点P'的坐标是（﹣3，2）．故选：B．【点睛】本题主要考查了关于原点对称的点的坐标的特点，正确掌握横纵坐标的关系是解题关键．3、A【分析】连结OC，根据切线长性质DC=AC，OC平分∠ACD，求出∠OCD=∠OCA==30°，利用在Rt△ABC中，AC=ABtanB=3×，在Rt△AOC中，∠ACO=30°，AO=ACtan30°=，利用三角形面积公式求出，，再求出扇形面积，利用割补法求即可．【详解】解：连结OC，∵以边上一点为圆心作，恰与边，分别相切于点A, ，∴DC=AC，OC平分∠ACD，∵，，∴∠ACD=90°-∠B=60°，∴∠OCD=∠OCA==30°，在Rt△ABC中，AC=ABtanB=3×，在Rt△AOC中，∠ACO=30°，AO=ACtan30°=，∴OD=OA=1，DC=AC=，∴，，∵∠DOC=360°-∠OAC-∠ACD-∠ODC=360°-90°-90°-60°=120°，∴，S阴影=．故选择A．【点睛】本题考查切线长性质，锐角三角形函数，扇形面积，三角形面积，角的和差计算，割补法求阴影面积，掌握切线长性质，锐角三角形函数，扇形面积，三角形面积，角的和差计算，割补法求阴影面积是解题关键．4、B【分析】由题意易得，然后根据三角形外角的性质可求解．【详解】解：由旋转的性质可得：，∴；故选B．【点睛】本题主要考查旋转的性质及三角形外角的性质，熟练掌握旋转的性质及三角形外角的性质是解题的关键．5、C【分析】根据⊙O的半径r=4，且点A到圆心O的距离d=5知d>r，据此可得答案．【详解】解：∵⊙O的半径r=4，且点A到圆心O的距离d=5，∴d>r，∴点A在⊙O外，故选：C．【点睛】本题主要考查点与圆的位置关系，点与圆的位置关系有3种．设⊙O的半径为r，点P到圆心的距离OP=d，则有：①点P在圆外⇔d＞r；②点P在圆上⇔d=r；③点P在圆内⇔d＜r．6、B【分析】根据关于原点对称的两个点，横坐标、纵坐标分别互为相反数，即可求解．【详解】解：平面直角坐标系中点关于原点对称的点的坐标是故选B【点睛】本题考查了关于原点对称的点的特征，掌握关于原点对称的两个点，横坐标、纵坐标分别互为相反数是解题的关键．7、C【分析】连接，过点作于点，交于点，先由垂径定理求出的长，再根据勾股定理求出的长，进而得出的长即可．【详解】解：连接，过点作于点，交于点，如图所示：则，的直径为，，在中，，，即水的最大深度为，故选：C．【点睛】本题考查了垂径定理、勾股定理等知识，解题的关键是根据题意作出辅助线，构造出直角三角形是解答此题的关键．8、A【详解】解：A、既是轴对称图形又是中心对称图形，此项符合题意；B、是中心对称图形，不是轴对称图形，此项不符题意；C、是轴对称图形，不是中心对称图形，此项不符题意；D、是轴对称图形，不是中心对称图形，此项不符题意；故选：A．【点睛】本题考查了中心对称图形和轴对称图形，熟记中心对称图形的定义（在平面内，把一个图形绕某点旋转，如果旋转后的图形与另一个图形重合，那么这两个图形互为中心对称图形）和轴对称图形的定义（如果一个图形沿一条直线折叠，直线两旁的部分能够完全重合，那么这个图形叫做轴对称图形）是解题关键．9、C【分析】过点A作AC⊥x轴于点C，设 ，则 ，根据勾股定理，可得，从而得到 ，进而得到∴ ，可得到点 ，再根据旋转的性质，即可求解．【详解】解：如图，过点A作AC⊥x轴于点C， 设 ，则 ，∵ ，，∴，∵， ，∴ ，解得： ，∴ ，∴ ，∴点 ，∴将绕原点O顺时针旋转90°，则旋转后点A的对应点的坐标是，∴将绕原点O逆时针旋转90°，则旋转后点A的对应点的坐标是．故选：C【点睛】本题考查坐标与图形变化一旋转，解直角三角形等知识，解题的关键是求出点A的坐标，属于中考常考题型．10、D【分析】根据轴对称图形与中心对称图形的概念求解．【详解】解：A、不是轴对称图形，不是中心对称图形，故此选项不符合题意；B、是轴对称图形，不是中心对称图形，故此选项不符合题意；C、是轴对称图形，是中心对称图形，故此选项不符合题意；D、不是轴对称图形，是中心对称图形，故此选项符合题意；故选：D．【点睛】此题主要考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．二、填空题1、12【分析】如图，连接BC，AO，作点P关于AB的对称点M，作点P关于AC的对称点N，连接MN交AB于E，交AC于F，此时△PEF的周长=PE+PF+EF=EM+EF+FM=MN，想办法求出MN的最小值即可解决问题．【详解】解：如图，连接BC，AO，作点P关于AB的对称点M，作点P关于AC的对称点N，连接MN交AB于E，交AC于F，此时△PEF的周长=PE+PF+EF=EM+EF+FM=MN，∴当MN的值最小时，△PEF的值最小，∵AP=AM=AN，∠BAM=∠BAP，∠CAP=∠CAN，∠BAC=60°，∴∠MAN=120°，∴MN=AM=PA，∴当PA的值最小时，MN的值最小，取AB的中点J，连接CJ．∵AB=8，AC=4，∴AJ=JB=AC=4，∵∠JAC=60°，∴△JAC是等边三角形，∴JC=JA=JB，∴∠ACB=90°，∴BC=，∵∠BOC=60°，OB=OC，∴△OBC是等边三角形，∴OB=OC=BC=4，∠BCO=60°，∴∠ACH=30°，∵AH⊥OH，AH=AC=2，CH=AH=2，∴OH=6，∴OA==4，∵当点P在直线OA上时，PA的值最小，最小值为-，∴MN的最小值为•（-）=-12．故答案：-12．【点睛】本题考查了圆周角定理，垂径定理，轴对称-最短问题等知识，解题的关键是学会利用轴对称解决最短问题，属于中考填空题中的压轴题．2、60【分析】正六边形连接各个顶点和中心，这些连线会将360°分成6分，每份60°因此至少旋转60°，正六边形就能与自身重合．【详解】360°÷6=60°故答案为：60【点睛】本题考查中心对称图形的性质，根据图形特征找到最少旋转度数是本题关键．3、60【分析】在Rt△BOE中，利用勾股定理求得OE=1，知OB=2OE，得到∠BOE=60°，∠BOC=120°，再利用圆周角定理即可解决问题．【详解】解：如图作OE⊥BC于E．∵OE⊥BC，∴BE=EC=，∠BOE=∠COE，∴OE=1，∴OB=2OE，∴∠OBE=30°，∴∠BOE=∠COE=60°，∴∠BOC=120°，∴∠BAC=60°，故答案为：60．【点睛】本题考查三角形的外心与外接圆、圆周角定理．垂径定理、勾股定理、直角三角形30度角性质、等腰三角形的性质等知识，解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题．4、【分析】根据题意作等边三角形的外接圆，当点运动到的中点时，四边形ADBC的面积S的最大值，分别求出两个三角形的面积，相加即可．【详解】解：根据题意作等边三角形的外接圆，D在运动过程中始终保持∠ADB＝120°不变，在圆上运动，当点运动到的中点时，四边形ADBC的面积S的最大值，过点作的垂线交于点，如图：，，，在中，，解得：，，过点作的垂线交于，，，，，故答案是：．【点睛】本题考查了等边三角形，外接圆、勾股定理、动点问题，解题的关键是，作出图象及掌握圆的相关性质．5、-2【分析】由图可知，当CN⊥AB且C、M、N三点共线时，长度最小，利用勾股定理求出CN的长，故可求解．【详解】由图可知，当CN⊥AB且C、M、N三点共线时，长度最小∵直线AB的解析式为当x=0时，y=5，当y=0时，x=5∴B（0，5），A（5，0）∴AO=BO，△AOB是等腰直角三角形∴∠BAO=90°当CN⊥AB时，则△ACN是等腰直角三角形∴CN=AN∵C∴AC=7∵AC2=CN2+AN2=2CN2∴CN=当 C、M、N三点共线时，长度最小即MN=CN-CM=-2故答案为：-2．【点睛】此题主要考查圆与几何综合，解题的关键是根据题意找到符合题意的位置，利用等腰直角三角形的性质求解．三、解答题1、（1）4；（2）-1或-7【分析】（1）如图，且三点在一条直线上的情况，连接，过点向作垂线交点为，在直角三角形中，，，可求的长；（2）如图，过点向作垂线交点为，过点作轴垂线交于点，作交点为；由，知，，点G坐标为，得，由知的值，从而得到的值．【详解】解：（1）∵∠DAD1＝30°且D1、C1、O三点在一条直线上∴如图所示，连接，过点向作垂线交点为∴∵．（2）如图过点向作垂线交点为，过点作轴垂线交于点，作交点为，在和中点横坐标可表示为∴p+q=-7或-1．【点睛】本题考查了锐角三角函数值，三角形全等,图形旋转的性质等知识．解题的关键与难点是找出线段之间的关系．2、（1）；（2）；（3）【分析】（1）如图，过作 垂足分别为 连接证明 四边形为正方形，可得 证明 可得答案；（2）先求解 再结合（1）的结论可得答案；（3）如图，连接 先求解 再证明 再求解 可得 再利用弧长公式计算即可.【详解】解：（1）如图，过作 垂足分别为 连接 四边形为矩形，由勾股定理可得： 而 四边形为正方形， 而 （2）如图，过作 垂足分别为 由（1）得：四边形为正方形， OA＝2，∠OAB＝15°， （3）如图，连接 【点睛】本题考查的是勾股定理的应用，等腰三角形的判定与性质，矩形，正方形的判定与性质，垂径定理的应用，弧长的计算，掌握以上知识并灵活运用是解本题的关键.3、（1）见解析；（2）CD=，EF=1．【分析】（1）连接OC，根据圆的性质，得到OB=OC；根据等腰三角形的性质，得到；根据平行线的性质，得到；在同圆和等圆中，根据相等的圆心解所对的弧等即得证．（2）根据直径所对的圆周角是直角求出∠ACB=90°，根据平行线的性质求得∠AEO=∠ACB=90°，利用勾股定理求出AC=8，根据垂径定理求得EC=AE=4，根据中位线定理求出OE，在Rt△CDE中，根据勾股定理求出CD，因为，所以△EDF∽△BCF，最后根据似的性质，列方程求解即可．【详解】（1）解：连结OC．∵∴∠1=∠B∠2=∠C∵OB =OC∴∠B=∠C∴∠1=∠2∴弧AD=弧CD（2）∵AB是的直径∴∠ACB=90°∵∴∠AEO=∠ACB=90°Rt△ABC中，∠ACB=90°，∵BC=6，AB=10 ∴AC=8∵半径OD⊥AC于E ∴EC=AE=4  OE=∴ED=2  由勾股定理得，CD=∵∴△EDF∽△CBF∴设EF=x，则FC=4-x∴EF=1，经检验符合题意.【点睛】本题考查了圆的综合题，圆的有关性质：圆的半径相等；同圆或等圆中，相等的圆心角所对的弧等；直径所对的圆周角是直角；垂径定理；平行线的性质，勾股定理，三角形中位线定理，三角形相似的判定和性质等知识，正确理解圆的相关性质是解题的关键．4、（1）①B和C；②或；（2）或【分析】（1）①分别找出点A，B，C到线段ON的最小值和最大值，是否满足“二分点”定义即可；②对a的取值分情况讨论：、、和，根据“二分点”的定义可求解；（2）设线段AN上存在的“二分点”为，对的取值分情况讨论、，、，和，根据“二分点”的定义可求解．【详解】（1）①∵点A在ON上，故最小值为0，不符合题意，点B到ON的最小值为，最大值为，∴点B是线段ON的“二分点”，点C到ON的最小值为1，最大值为，∴点C是线段ON的“二分点”，故答案为：B和C；②若时，如图所示：点C到OD的最小值为，最大值为，∵点C为线段OD的“二分点”，∴，解得：；若，如图所示：点C到OD的最小值为1，最大值为，满足题意；若时，如图所示：点C到OD的最小值为1，最大值为，∵点C为线段OD的“二分点”，∴，解得：（舍）；若时，如图所示：点C到OD的最小值为，最大值为，∵点C为线段OD的“二分点”，∴，解得：或（舍），综上所得：a的取值范围为或；（2）如图所示，设线段AN上存在的“二分点”为，当时，最小值为：，最大值为：，∴，即，∵，∴∴；当，时，最小值为：，最大值为：，∴∴，即，∵，∴，∵，∴不存在；当，时，最小值为：，最大值为：，∴，即，∴，∵，∴不存在；当时，最小值为：，最大值为：，∴，即，∴，∵，∴，综上所述，r的取值范围为或．【点睛】本题考查坐标上的两点距离，解一元二次方程解不等式以及点到圆的距离求最值，根据题目所给条件，掌握“二分点”的定义是解题的关键．5、（1），（2）．【分析】（1）根据弦AB垂直平分半径OC，OC=OB=10cm，得出OD=CD=，∠ODB=90°，根据勾股定理，可求AB=2BD=2×；（2）根据锐角三角函数定义求出cos∠DOB=，得出∠DOB=60°，利用弧长公式求出即可．【详解】解：（1）∵弦AB垂直平分半径OC，OC=OB=10cm，∴OD=CD=，∠ODB=90°，∴，∴AB=2BD=2×，故答案为；（2）cos∠DOB=，∴∠DOB=60°，∴的度数为2×60°=120°，∴．【点睛】本题考查垂直平分线性质，勾股定理，锐角三角函数，弧长，掌握垂直平分线性质，勾股定理，锐角三角函数，弧长是解题关键．