

初中数学人教版九年级下册26.1.1 反比例函数同步达标检测题
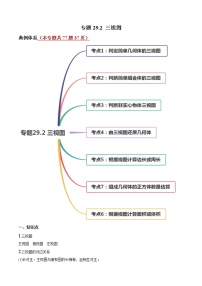
展开专题26.1 反比例函数
典例体系(本专题共45题35页)
一、知识点
1.反比例函数的概念:一般地,(k为常数,k≠0)叫做反比例函数,即y是x的反比例函数。
(x为自变量,y为因变量,其中x不能为零)
2.反比例函数的等价形式:y是x的反比例函数 ←→ ←→ ←→ ←→ 变量y与x成反比例,比例系数为k..版权所有
3.判断两个变量是否是反比例函数关系有两种方法:①按照反比例函数的定义判断;②看两个变量的乘积是否为定值<即>。(通常第二种方法更适用)
4.反比例函数的图象由两条曲线组成,叫做双曲线
反比例函数的画法的注意事项:①反比例函数的图象不是直线,所“两点法”是不能画的;
②选取的点越多画的图越准确;
③画图注意其美观性(对称性、延伸特征)。
5.反比例函数性质:
①当k>0时,双曲线的两支分别位于一、三象限;在每个象限内,y随x的增大而减小;
②当k<0时,双曲线的两支分别位于二、四象限;在每个象限内,y随x的增大而增大;
③双曲线的两支会无限接近坐标轴(x轴和y轴),但不会与坐标轴相交。
6.反比例函数图象的几何特征:(如图4所示)
点P(x,y)在双曲线上都有
P
B
A
O
P
B
A
O
图4
二、考点点拨与训练
考点1:反比例函数的定义及应用
典例:(2019·湖南澧县·初三月考)已知函数y = y1 +y2,y1与x成反比例,y2与x-2成正比例,且当x =1时,y = -1,当x = 3时,y = 3. 求y关于x的函数解析式.
方法或规律点拨
本题考查待定系数法求函数解析式,关键是掌握待定系数法求函数解析式的方法.
巩固练习
1.(2020·青浦区实验中学初二期中)已知,与成正比例,与成反比例,当时,;时,.求:关于的函数解析式
2.(2020·全国初三课时练习)已知函数
(1)如果y是x的正比例函数,求m的值;
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
3.(2020·芜湖市第二中学初三期末)已知函数解析式为y=(m-2)
(1)若函数为正比例函数,试说明函数y随x增大而减小
(2)若函数为二次函数,写出函数解析式,并写出开口方向
(3)若函数为反比例函数,写出函数解析式,并说明函数在第几象限
4.(2020·江西余干·初三零模)已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
5.(2019·全国初二课时练习)已知,是的反比例函数,是的正比例函数,当时,;当时,.
(1)求与的函数关系式;
(2)当时,求的值.
6.(2018·浙江金东·初二期末)已知:y=y1﹣y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时y=1.
(1)求y关于x的函数关系式.
(2)求x=﹣时,y的值.
7.(2019·江苏兴化·初二月考)已知y=y1-y2, y1与x+2成正比例,y2与x2成反比例.当x=-1时,y=-2;当x=1时,y=2.
(1)求y与x的函数关系式.
(2)当x=时,求y的值
8.已知y=(m-2)x|m|-3是反比例函数,则m是什么?
9.(2019·全国初二课时练习)当m为何值时,函数y=(m﹣3)x2﹣|m|是反比例函数?当m为何值时,此函数是正比例函数?
10.(2019·全国初三单元测试)已知函数.
若它是正比例函数,求的值;
若它是反比例函数,求m的值
考点2:确定反比例函数解析式
典例:(2019·广东深圳实验学校初三开学考试)如图,在平面直角坐标系中,矩形的顶点的坐标为,顶点的坐标为,将矩形绕点逆时针旋转,使点落在轴的点处,得到矩形,与交于点.
(1)求图象经过点的反比例函数的解析式;
(2)设(1)中的反比例函数图象交于点,求出直线的解析式.
方法或规律点拨
本题主要考查相似三角形的判定与性质,能够运用待定系数法求得函数的解析式,根据函数的解析式确定点的坐标.
巩固练习
1.(2018·河北初三其他)某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该反比例函数的表达式.
(2)当气体体积为1m3时,气球内气体的气压是多少?
(3)当气球内的气压大于200kPa时,气球将爆炸,为确保气球不爆炸,气球内气体的体积应不小于多少?
2.(2019·全国初三单元测试)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.求反比例函数的解析式.
3.(2019·全国初三期末)如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)求△MOB的面积.
4.(2019·江苏常熟·初二期末)点 P(-2,4)关于 y 轴的对称点 P'在反比例函数 y=(k≠0)的图象上.
(1)求此反比例函数关系式;
(2)当 x 在什么范围取值时,y 是小于 1 的正数?
5.(2019·河南镇平·初二期中)已知反比例函数y=的图象经过A(2,﹣4).
(1)求k的值;
(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?
6.(2020·江苏无锡·初二期末)如图,已知点、都在反比例函数的图像上.
(1)求和的值;
(2)以为一边在第一象限内作,若点的横坐标为,且的面积为,求点的坐标.
7.(2019·济宁市第十五中学初三月考)如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=(x>0)和y=(x<0)的图象交于点P、点Q.
(1)求点P的坐标;
(2)若△POQ的面积为8,求k的值.
考点3:反比例函数增减性的应用
典例:(2020·河北青龙·月考)已知反比例函数(为常数,且).
(1)若在其图象的每一个分支上,的值随的值增大而减小,求的取值范围;
(2)若点在该反比例函数的图象上.
①求的值;
②当时,直接写出的取值范围.
方法或规律点拨
本题考查了反比例函数图象的性质、待定系数法求解析式,求函数的取值范围时,数形结合是关键.
巩固练习
1.(2019·全国初三单元测试)已知反比例函数的图象在所在的每一个象限内,y随x的增大而增大,求该反比例函数的表达式.
2.(2019·天津市北仓第二中学初三月考)已知点P(2,6)在反比例函数()的图象上.
(1)当时,求的值;(2)当时,求的取值范围.
3.k为何值时,函数是反比例函数?k为何值时在每一象限内y随x的增大而增大?k为何值时在每一象限内y随x的增大而减小?
4.(2019·沙雅县第一中学初三月考)已知反比例函数(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
5.(2019·涡阳县王元中学初三月考)已知反比例函数y=的图像经过点A(2,-4).
(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 (填变化情况);
(3)当≤x≤2时,求y的取值范围.
6.(2020·河南遂平·初二期中)如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=的图象上,当-3≤x≤-1时,求函数值y的取值范围.
7.(2020·江苏沭阳·初二期末)已知反比例函数y=的图象经过点和.点和也在比反比例函数的图象上,且x1<x2.
(1)求n和k的值;
(2)试比较y1与y2的大小.
8.(2019·全国初二单元测试)已知函数.
(1)当为何值时,它是正比例函数,且随的减小而减小;
(2)当为何值时,它是反比例函数,且函数图像在第一、三象限.
考点4:由图形面积求比例系数
典例:(2020·浙江北仑·)如图,已知点A(2,m)是反比例函数y=的图象上一点,过点A作x轴的垂线,垂足为B,连结OA,△ABO的面积为6.
(1)求k和m的值;
(2)直线y=2x+a(a≤0)与直线AB交于点C与反比例函数图象交于点E,F;
①若a=0,已知E(p,q),则F的坐标为 (用含p,q的坐标表示);
②若a=﹣2.求AC的长.
方法或规律点拨
本题考查了反比例函数系数k的几何意义、反比例函数的性质以及函数图象上点的坐标特点等知识,属于基本知识题型,熟练掌握反比例函数的图象与性质及其系数k的几何意义是解题关键.
巩固练习
1.(2020·河北青县·初三其他)如图,已知双曲线经过斜边的中点,与直角边相交于点,若的面积为3,求的值.
2.(2020·广东初三二模)如图,等边△ABC的顶点A,B分别在双曲线y=的两个分支上,且AB经过原点O.BD⊥x轴于D,S△BOD=2.
(1)直接写出该双曲线的解析式为_______;
(2)若OD=2,求A、B、C点的坐标.
3.(2016·江苏海安·初三月考)如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,
(1)求四边形DCEB的面积.
(2)求k的值.
4.(2020·河北)如图,已知反比例函数的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为4.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数的图象上,当y≤2(y≠0)时,求自变量x的取值范围.
考点5:已知反比例函数求面积
典例:.(2020·湖北利川·)已知,反比例函数和的部分图象如图所示,点P在上,PC垂直x轴于点C,交于点A(2,1),PD垂直y轴于点D,交于点B,连接OA,OB.
(1)求B点和P点的坐标;
(2)求四边形AOBP的面积.
方法或规律点拨
本题考查了反比例函数的图像和性质,矩形的性质,以及利用间接法求四边形的面积,解题的关键是熟练掌握反比例函数的性质进行解题.
巩固练习
1.(2018·全国初三单元测试)如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P(1,4)在C1上,PA⊥x轴于点A,交C2于点B(1,m),求k,m的值及△POB的面积.
2.(2020·四川双流·初三其他)如图,在平面直角坐标系中,正比例函数y=x的图像与反比例函数y=的图像交于A,B两点,且点A的坐标为(6,a).
(1)求反比例函数的表达式;
(2)已知点C(b,4)在反比例函数y=的图像上,点P在x轴上,若△AOC的面积等于△AOP的面积的两倍,请求出点P的坐标.
2.(2020·河南西华·初三一模)小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到下表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
■
3
2
1.5
1
0.5
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_________;
(2)y与x的函数关系式为_________,且y随x的增大而_________;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形的面积记为,矩形的面积记为,请判断与的大小关系,并说明理由;
(4)在(3)的条件下,交于点G,反比例函数的图象经过点G交于点H,连接、,则四边形的面积为_________.
3.如图,点在双曲线的第一象限的那一支上,垂直于轴于点,点在轴正半轴上,且,点在线段上,且,点为的中点,若的面积为3,则的值为______.
4.(2019·石家庄市第十七中学初三期中)如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
5.(2019·河北桥东·邢台三中初三月考)已知反比例函数y=的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
6.(2019·河北保定·初三期末)如图所示,点A(,3)在双曲线y=上,点B在双曲线y=之上,且AB∥x轴,C,D在x轴上,若四边形ABCD为矩形,求它的面积.
7.(2019·甘肃天水·初三期中)如图所示,双曲线经过斜边上的点,且满足,与交于点,,求的值.
8.(2018·全国初三单元测试)如图.矩形的边,在坐标轴上,顶点在第一象限,反比例函数的图象经过的中点,交于点,且四边形的面积为.求的值.
9.(2019·全国初三单元测试)如图,若点在反比例函数的图象上,轴于点,的面积为.
求的值;
当点在反比例函数图象上运动,其它条件不变,的面积发生变化吗?并说明你的理由.
10.(2018·全国初三期末)已知反比例函数的图象如图所示,点,是该图象上的两点.
(1)求的取值范围;
(2)比较与的大小;
(3)若点在该反比例函数图象上,求此反比例函数的解析式;
(4)若为第一象限上的一点,作轴于点,求的面积(用含的式子表示)
11. (2020·大石桥市周家镇中学初三月考)已知反比例函数y=(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D
(1)求这个反比函数的表达式;
(2)求△ACD的面积.
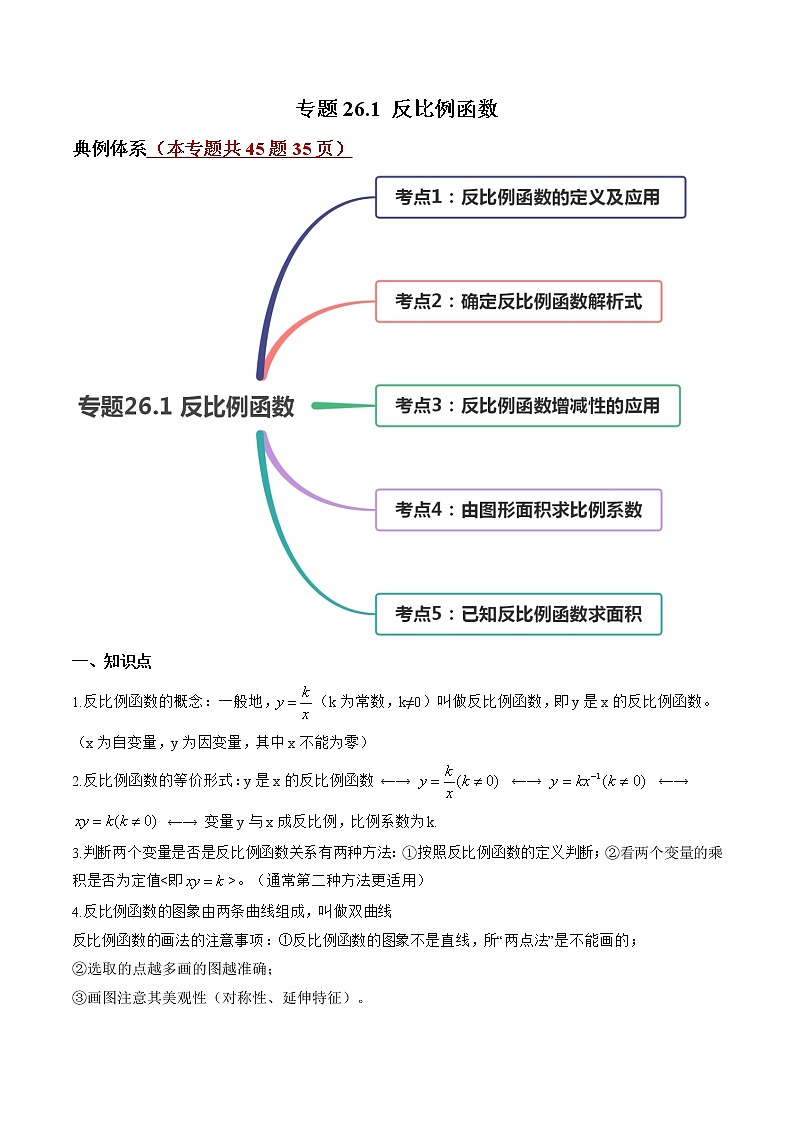
专题26.1 反比例函数
典例体系(本专题共45题35页)
一、知识点
1.反比例函数的概念:一般地,(k为常数,k≠0)叫做反比例函数,即y是x的反比例函数。
(x为自变量,y为因变量,其中x不能为零)
2.反比例函数的等价形式:y是x的反比例函数 ←→ ←→ ←→ ←→ 变量y与x成反比例,比例系数为k.
3.判断两个变量是否是反比例函数关系有两种方法:①按照反比例函数的定义判断;②看两个变量的乘积是否为定值<即>。(通常第二种方法更适用)
4.反比例函数的图象由两条曲线组成,叫做双曲线
反比例函数的画法的注意事项:①反比例函数的图象不是直线,所“两点法”是不能画的;
②选取的点越多画的图越准确;
③画图注意其美观性(对称性、延伸特征)。
5.反比例函数性质:
①当k>0时,双曲线的两支分别位于一、三象限;在每个象限内,y随x的增大而减小;
②当k<0时,双曲线的两支分别位于二、四象限;在每个象限内,y随x的增大而增大;
③双曲线的两支会无限接近坐标轴(x轴和y轴),但不会与坐标轴相交。
6.反比例函数图象的几何特征:(如图4所示)
点P(x,y)在双曲线上都有
P
B
A
O
P
B
A
O
图4
二、考点点拨与训练
考点1:反比例函数的定义及应用
典例:(2019·湖南澧县·初三月考)已知函数y = y1 +y2,y1与x成反比例,y2与x-2成正比例,且当x =1时,y = -1,当x = 3时,y = 3. 求y关于x的函数解析式.
【答案】
【解析】解:∵y=y1+y2,其中y1与x成反比例,y2与(x-2)成正比例,
∴设出y1=,y2=k2(x-2),(k1≠0,k2≠0),则y=+k2(x-2),
把当x=1时,y=-1;x=3时,y=3代入得:
解得:
.
方法或规律点拨
本题考查待定系数法求函数解析式,关键是掌握待定系数法求函数解析式的方法.
巩固练习
1.(2020·青浦区实验中学初二期中)已知,与成正比例,与成反比例,当时,;时,.求:关于的函数解析式
【答案】
【解析】解:设,,
则,
根据题意得:,
解得:,
则函数解析式是:.
2.(2020·全国初三课时练习)已知函数
(1)如果y是x的正比例函数,求m的值;
(2)如果y是x的反比例函数,求出m的值,并写出此时y与x的函数关系式.
【答案】(1)m=2或m=﹣1(2)y=3x﹣1
【解析】(1)由y=(m2+2m)是正比例函数,得
m2﹣m﹣1=1且m2+2m≠0,
解得m=2或m=﹣1;
(2)由y=(m2+2m)是反比例函数,得
m2﹣m﹣1=﹣1且m2+2m≠0,
解得m=1.
故y与x的函数关系式y=3x﹣1 .
3.(2020·芜湖市第二中学初三期末)已知函数解析式为y=(m-2)
(1)若函数为正比例函数,试说明函数y随x增大而减小
(2)若函数为二次函数,写出函数解析式,并写出开口方向
(3)若函数为反比例函数,写出函数解析式,并说明函数在第几象限
【答案】(1)详见解析;(2)y=-4x2,开口向下;(3)y=-x-1或y=-3x-1,函数在二四象限
【解析】
解:(1)若为正比例函数则 -2=1,m=±,
∴m-2<0,函数y随x增大而减小;
(2) 若函数为二次函数,-2=2且m-2≠0,
∴m=-2,函数解析式为y=-4x2,开口向下
(3)若函数为反比例函数,-2=-1, m=±1, m-2<0,
解析式为y=-x-1或y=-3x-1,函数在二四象限
4.(2020·江西余干·初三零模)已知y=y1+y2,y1与x+1成正比例,y2与x+1成反比例,当x=0时,y=﹣5;当x=2时,y=﹣7.
(1)求y与x的函数关系式;
(2)当x=5时,求y的值.
【答案】(1);(2).
【解析】(1)∵y1与x+1成正比例,y2与x+1成反比例,
设y1=a(x+1)(a≠0),y2= (b≠0).
∵y=y1+y2,∴y=a(x+1)+ ,
把(0,﹣5),(2,﹣7)代入得:,
解得:,∴y=﹣2(x+1)﹣,
答:y与x的函数关系式是y=﹣2(x+1)﹣.
(2)当x=5时,y=﹣2(x+1)﹣=﹣2×(5+1)﹣=﹣12 ,
答:当x=5时,y的值是﹣12.
5.(2019·全国初二课时练习)已知,是的反比例函数,是的正比例函数,当时,;当时,.
(1)求与的函数关系式;
(2)当时,求的值.
【答案】(1);(2)18.
【解析】(1)设,,则 解得 故.
(2)当时,
6.(2018·浙江金东·初二期末)已知:y=y1﹣y2,y1与x2成正比例,y2与x成反比例,且x=1时,y=3;x=﹣1时y=1.
(1)求y关于x的函数关系式.
(2)求x=﹣时,y的值.
【答案】(1)y=2x2+;(2)y=﹣.
【解析】解:(1)设y1=k1x2,y2=,
∵y=y1﹣y2,
∴y=k1 x2﹣,
把x=1,y=3代入y=k1 x2﹣得:k1﹣k2=3①,
把x=﹣1,y=1代入y=k1 x2﹣得:k1 + k2=1②,
①,②联立,解得:k1=2,k2=﹣1,
即y关于x的函数关系式为y=2x2+,
(2)把x=﹣代入y=2x2+,
解得y=﹣.
7.(2019·江苏兴化·初二月考)已知y=y1-y2, y1与x+2成正比例,y2与x2成反比例.当x=-1时,y=-2;当x=1时,y=2.
(1)求y与x的函数关系式.
(2)当x=时,求y的值
【答案】(1) ;(2)-11
【解析】
(1)设y1= a(x+2),y2=,则y= a(x+2)-,
把x=﹣1,y=-2;x=1,y=2分别代入得,解得,
所以y与x之间的函数关系为;
(2)当x=时, .
8.已知y=(m-2)x|m|-3是反比例函数,则m是什么?
【答案】.
【解析】∵y=(m-2)x|m|-3是反比例函数,
∴,
解得:.
9.(2019·全国初二课时练习)当m为何值时,函数y=(m﹣3)x2﹣|m|是反比例函数?当m为何值时,此函数是正比例函数?
【答案】m=﹣3时,函数y=(m﹣3)x2﹣|m|是反比例函数;当m=±1,此函数是正比例函数
【解析】根据反比例函数的定义知2﹣|m|=﹣1,m﹣3≠0,
解得:m=﹣3;
根据正比例函数的定义知2﹣|m|=1,m﹣3≠0,
解得:m=±1.
故答案为:m=﹣3时,函数y=(m﹣3)x2﹣|m|是反比例函数;当m=±1,此函数是正比例函数.
10.(2019·全国初三单元测试)已知函数.
若它是正比例函数,求的值;
若它是反比例函数,求m的值
【答案】(1)3;(2).
【解析】
是正比例函数,
,
,
是反比例函数,
,,
.
考点2:确定反比例函数解析式
典例: (2019·广东深圳实验学校初三开学考试)如图,在平面直角坐标系中,矩形的顶点的坐标为,顶点的坐标为,将矩形绕点逆时针旋转,使点落在轴的点处,得到矩形,与交于点.
(1)求图象经过点的反比例函数的解析式;
(2)设(1)中的反比例函数图象交于点,求出直线的解析式.
【答案】(1) (2)
【解析】解:(1)∵∠OGA=∠M=90°,∠GOA=∠MON
∴△OGA∽△OMN,
∴ ∴ , 解得AG=1.
设反比例函数,把A(1,2)代入得k=2,
∴过点A的反比例函数的解析式为:.
(2)∵点B的横坐标为4,x=4代 中,故(4,)
设直线AB的解析式y=mx+n,把A(1,2)、B(4,)代入,
得 , 解得 .
∴直线AB的解析式.
方法或规律点拨
本题主要考查相似三角形的判定与性质,能够运用待定系数法求得函数的解析式,根据函数的解析式确定点的坐标.
巩固练习
1.(2018·河北初三其他)某气球内充满了一定量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
(1)求该反比例函数的表达式.
(2)当气体体积为1m3时,气球内气体的气压是多少?
(3)当气球内的气压大于200kPa时,气球将爆炸,为确保气球不爆炸,气球内气体的体积应不小于多少?
【答案】(1) ;(2)96kPa;(3) .
【解析】解:(1)设ρ=,由题意知120=,所以k=96,故ρ=(v>0);
(2)当v=1m3时,ρ==96,∴气球内气体的气压是96kPa;
(3)当p=200kPa时,v==.
所以为了安全起见,气体的体积应不少于m3.
2.(2019·全国初三单元测试)如图,在平面直角坐标系中,将坐标原点O沿x轴向左平移2个单位长度得到点A,过点A作y轴的平行线交反比例函数y=的图象于点B,AB=.求反比例函数的解析式.
【答案】反比例函数的解析式为y=-.
【解析】∵将坐标原点O沿x轴向左平移2个单位长度得到点A,
∴OA=2,
∵AB//y轴,AB=,
∴B点坐标为:(-2,),
把B(-2,),代入y=中,得到k=-3,
∴反比例函数的解析式为y=-.
3.(2019·全国初三期末)如图,一次函数y1=﹣x﹣1的图象与x轴交于点A,与y轴交于点B,与反比例函数y2=图象的一个交点为M(﹣2,m).
(1)求反比例函数的解析式;
(2)求△MOB的面积.
【答案】(1);(2)1
【解析】解:(1)∵M(﹣2,m)在一次函数y1=﹣x﹣1的图象上,
∴代入得:m=﹣(﹣2)﹣1=1,
∴M的坐标是(﹣2,1),
把M的坐标代入y2=得:k=﹣2,
即反比例函数的解析式是:;
(2)y1=﹣x﹣1,
当x=0时,y1=﹣1,
即B的坐标是(0,﹣1),
所以OB=1,
∵M(﹣2,1),
∴点M到OB的距离是2,
∴△MOB的面积是×1×2=1.
4.(2019·江苏常熟·初二期末)点 P(-2,4)关于 y 轴的对称点 P'在反比例函数 y=(k≠0)的图象上.
(1)求此反比例函数关系式;
(2)当 x 在什么范围取值时,y 是小于 1 的正数?
【答案】(1)y=;(2)x>8;
【解析】(1)∵点P(-2,4)与点P′关于y轴对称,
∴P′(2,4),
∵点P′在反比例函数y=(k≠0)的图象上,
∴4=,解得k=8,
∴反比例函数的关系式为:y=;
(2)∵y是小于1的正数,
∴0<<1,解得x>8.
5.(2019·河南镇平·初二期中)已知反比例函数y=的图象经过A(2,﹣4).
(1)求k的值;
(2)这个函数的图象在哪几个象限?y随x的增大怎样变化?
【答案】(1)k=9;(2)图象位于二、四象限,在每个象限内y随x的增大而增大.
【解析】解:(1)∵反比例函数y=的图象经过A(2,﹣4),
∴1﹣k=2×(﹣4)=﹣8;
解得:k=9;
(2)∵1﹣k=﹣8<0,
∴图象位于二、四象限,在每个象限内y随x的增大而增大.
6.(2020·江苏无锡·初二期末)如图,已知点、都在反比例函数的图像上.
(1)求和的值;
(2)以为一边在第一象限内作,若点的横坐标为,且的面积为,求点的坐标.
【答案】(1),;(2)
【解析】解:(1)把,代入,解得:.
把代入,解得:,.
(2)∵点横坐标为,设.
连,过点作轴,作,,则,,
∵,或,
,或,
解得:,.
7.(2019·济宁市第十五中学初三月考)如图,在平面直角坐标系中,过点M(0,2)的直线l与x轴平行,且直线l分别与反比例函数y=(x>0)和y=(x<0)的图象交于点P、点Q.
(1)求点P的坐标;
(2)若△POQ的面积为8,求k的值.
【答案】(1)点坐标为;(2).
【解析】解:∵轴,
∴点的纵坐标为,
把代入得,
∴点坐标为;
∵,
∴,
∴,
而,
∴.
考点3:反比例函数增减性的应用
典例:(2020·河北青龙·月考)已知反比例函数(为常数,且).
(1)若在其图象的每一个分支上,的值随的值增大而减小,求的取值范围;
(2)若点在该反比例函数的图象上.
①求的值;
②当时,直接写出的取值范围.
【答案】(1)的取值范围为;(2)①的值为6;②的取值范围为.
【解析】解:(1)∵在图象的每一个分支上,的值随的值增大而减小,
∴,
∴;
(2)①∵点在该反比例函数图像上,
∴,
∴,
②反比例函数解析式为,
当时,,
由图可得,当时,.
方法或规律点拨
本题考查了反比例函数图象的性质、待定系数法求解析式,求函数的取值范围时,数形结合是关键.
巩固练习
1.(2019·全国初三单元测试)已知反比例函数的图象在所在的每一个象限内,y随x的增大而增大,求该反比例函数的表达式.
【答案】.
【解析】解:∵反比例函数的图象在所在的每一个象限内,y随x的增大而增大,
∴,解得,
∴,
∴该反比例函数的表达式为:.
2.(2019·天津市北仓第二中学初三月考)已知点P(2,6)在反比例函数()的图象上.
(1)当时,求的值;(2)当时,求的取值范围.
【答案】(1)当x=−3时,y=−4.(2)当1
∴,即k=12,
∴反比例函数的解析式为.
∴当x=−3时,y=−4.
(2)∵当x=1时,y=12;当x=3时,y=4,
又反比例函数,在x>0时,y值随x值的增大而减小,
∴当1
【答案】k=0或k=-1时是反比例函数;k=-1时在每一象限内y随x的增大而增大;
k=0时在每一象限内y随x的增大而减小
【解析】(1)∵y与x是反比例函数,
∴ ,解得k=0或k=-1;
(2)当<0,即<-时,在每一象限内y随x的增大而增大,所以k=-1;
(3)当>0,即>-时,在每一象限内y随x的增大而减小, 所以k=0.
4.(2019·沙雅县第一中学初三月考)已知反比例函数(k为常数,k≠1).
(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
【答案】(Ⅰ)5(Ⅱ)k>1(Ⅲ)x1>x2
【解析】解:(Ⅰ)由题意,设点P的坐标为(m,2)
∵点P在正比例函数y=x的图象上,∴2=m,即m=2.
∴点P的坐标为(2,2).
∵点P在反比例函数的图象上,∴,解得k=5.
(Ⅱ)∵在反比例函数图象的每一支上,y随x的增大而减小,
∴k-1>0,解得k>1.
(Ⅲ)∵反比例函数图象的一支位于第二象限,
∴在该函数图象的每一支上,y随x的增大而增大.
∵点A(x1,y1)与点B(x2,y2)在该函数的第二象限的图象上,且y1>y2,
∴x1>x2.
(1)设点P的坐标为(m,2),由点P在正比例函数y=x的图象上可求出m的值,从而得出P点坐标,再根据点P在反比例函数的图象上,所以,解得k=5.
(2)由于在反比例函数图象的每一支上,y随x的增大而减小,故k-1>0,求出k的取值范围即可.
(3)反比例函数图象的一支位于第二象限,故在该函数图象的每一支上,y随x的增大而增大,所以A(x1,y1)与点B(x2,y2)在该函数的第二象限的图象上,且y1>y2,故可知x1>x2.
5.(2019·涡阳县王元中学初三月考)已知反比例函数y=的图像经过点A(2,-4).
(1)求k的值;
(2)它的图象在第 象限内,在各象限内,y随x增大而 (填变化情况);
(3)当≤x≤2时,求y的取值范围.
【答案】(1)9;(2)二、四,增大;(3)
【解析】解:(1)依题意得:1﹣k=2×(﹣4)=﹣8,所以k=9;
(2)∵1﹣k=﹣8<0,
∴反比例函数y=的图象经过第二、四象限,且在各象限内,y随x增大而增大;
故答案是:二、四,增大;
(3)由(1)得反比例函数表达式为y=−,
当x=2时,y=-4,
当x=时,y= -16,
所以,当≤x≤2时,.
6.(2020·河南遂平·初二期中)如图,已知反比例函数y=的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为2.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数y=的图象上,当-3≤x≤-1时,求函数值y的取值范围.
【答案】(1) k=4, m=1;(2)当-3≤x≤-1时,y的取值范围为-4≤y≤-.
【解析】(1)∵△AOB的面积为2,∴k=4,∴反比例函数解析式为,∵A(4,m),∴m==1;
(2)∵当x=﹣3时,y=﹣;
当x=﹣1时,y=﹣4,又∵反比例函数在x<0时,y随x的增大而减小,∴当﹣3≤x≤﹣1时,y的取值范围为﹣4≤y≤﹣.
7.(2020·江苏沭阳·初二期末)已知反比例函数y=的图象经过点和.点和也在比反比例函数的图象上,且x1<x2.
(1)求n和k的值;
(2)试比较y1与y2的大小.
【答案】(1),;(2)当或时,y1<y2;当时,y1>y2
【解析】(1)将点和 代入反比例函数y=
即
解得
∴n和k的值分别为:,;
(2)∵n和k的值分别为:,
∴反比例函数解析式为:
∵点和也在比反比例函数的图象上
∴,
∴
∵
∴
∴当或时,
∴
即y1<y2
当时,
∴
即y1>y2.
8.(2019·全国初二单元测试)已知函数.
(1)当为何值时,它是正比例函数,且随的减小而减小;
(2)当为何值时,它是反比例函数,且函数图像在第一、三象限.
【答案】(1);(2).
【解析】(1)由已知可得:,解得:或,
又随的减小而减小,
,即,
,
(2)由已知可得:,解得:或,又∵函数图像在第一、三象限,
,即,或,.
考点4:由图形面积求比例系数
典例:(2020·浙江北仑·)如图,已知点A(2,m)是反比例函数y=的图象上一点,过点A作x轴的垂线,垂足为B,连结OA,△ABO的面积为6.
(1)求k和m的值;
(2)直线y=2x+a(a≤0)与直线AB交于点C与反比例函数图象交于点E,F;
①若a=0,已知E(p,q),则F的坐标为 (用含p,q的坐标表示);
②若a=﹣2.求AC的长.
【答案】(1)k=12,m=6;(2)①(﹣p,﹣q);②4.
【解析】解:(1)∵点A(2,m)是反比例函数y=的图象上一点,过点A作AB⊥x轴于点B,
∴S△AOB=|k|=6,
∴|k|=2×6=12,
∵图象在第一、三象限,∴k=12,
∴反比例函数为y=,
∴2m=12,解得:m=6;
(2)①若a=0,则y=2x是正比例函数,
∵直线y=2x与反比例函数图象交于点E,F,且E(p,q),
∴F(﹣p,﹣q),
故答案为(﹣p,﹣q);
②若a=﹣2,则函数为y=2x﹣2,
把x=2代入y=2x﹣2得,y=2,
∴C(2,2),
∵A(2,6),
∴AC=6﹣2=4.
方法或规律点拨
本题考查了反比例函数系数k的几何意义、反比例函数的性质以及函数图象上点的坐标特点等知识,属于基本知识题型,熟练掌握反比例函数的图象与性质及其系数k的几何意义是解题关键.
巩固练习
1.(2020·河北青县·初三其他)如图,已知双曲线经过斜边的中点,与直角边相交于点,若的面积为3,求的值.
【答案】
【解析】解:过点做轴,垂足为,
∵中,,
∴
∵为斜边的中点,
∴为的中位线
∴且
∵双曲线的解析式是
∴,
解得
2.(2020·广东初三二模)如图,等边△ABC的顶点A,B分别在双曲线y=的两个分支上,且AB经过原点O.BD⊥x轴于D,S△BOD=2..版权所有
(1)直接写出该双曲线的解析式为_______;
(2)若OD=2,求A、B、C点的坐标.
【答案】(1)y=﹣;(2)C(2,2).
【解析】解:(1)∵点B在双曲线y=的图象上,且BD⊥x轴于D,
∴S△BOD=|k|,
∵S△BOD=2,
∴|k|=4,
∵图象在二四象限,
∴k=﹣4,
∴反比例函数的解析式为y=﹣,
故答案为y=﹣;
(2)作CE⊥x轴于E,连接OC,
∵OD=2,
∴B的横坐标为2,
把x=2代入y=﹣,求得y=﹣2,
∴B(2,﹣2),
∵A、B关于原点对称,
∴A(﹣2,2),
∵反比例函数的图象关于原点对称,
∴OA=OB,
∵△ABC是等边三角形,
∴OC⊥AB,
∴∠BOC=90°,∠BCO=30°,
∴tan∠BCO==,
∴∠COE+∠BOD=90°,
∵CE⊥x轴,BD⊥x轴,
∴∠CEO=∠ODB=∠COE+∠OCE=90°,
∴∠BOD=∠OCE,
∴△COE∽△OBD,
∴,即,
∴OE=CE=2,
∴C(2,2).
3.(2016·江苏海安·初三月考)如图,A、B是双曲线y=上的两点,过A点作AC⊥x轴,交OB于D点,垂足为C,过B点作BE⊥x轴,垂足为E.若△ADO的面积为1,D为OB的中点,
(1)求四边形DCEB的面积.
(2)求k的值.
【答案】(1)1;(2).
【解析】(1)∵A、B是双曲线y=上的两点,BE⊥x轴,AC⊥x轴,
∴,
∴,
即,
又∵,
∴;
(2)∵D为OB的中点,BE⊥x轴,AC⊥x轴,
∴CD是△OBE的中位线,即CD=BE.
设A(x,),则B(2x,),
则CD=,AD=-,
∵△ADO的面积为1,
∴AD•OC=1,
即(-)•x=1,
解得k=.
4.(2020·河北)如图,已知反比例函数的图象经过点A(4,m),AB⊥x轴,且△AOB的面积为4.
(1)求k和m的值;
(2)若点C(x,y)也在反比例函数的图象上,当y≤2(y≠0)时,求自变量x的取值范围.
【答案】(1),;(2)在第一象限:当时,;在第三象限:当时,
【解析】解:(1)的面积为4,
,
反比例函数解析式为,
(2)当时,;
∴或.
∴答案为:在第一象限:当时,,在第三象限:当时,
考点5:已知反比例函数求面积
典例:.(2020·湖北利川·)已知,反比例函数和的部分图象如图所示,点P在上,PC垂直x轴于点C,交于点A(2,1),PD垂直y轴于点D,交于点B,连接OA,OB.
(1)求B点和P点的坐标;
(2)求四边形AOBP的面积.
【答案】(1)B点的坐标为(,3),P点的坐标为(2,3);(3)4
【解析】解:(1)由题意知,P点的横坐标与A(2,1)相同,纵坐标与B相同,
∵P点在上,把代入得,
∴P点的坐标为(2,3),B点的纵坐标为3.
又∵B点在上,把代入得,
∴B点的坐标为(,3),P点的坐标为(2,3).
(2)如图,由(1)知OC=2,OD=3,AC=1,BD=,
用S表示图形的面积,由题意得:
,
,
,
=4.
方法或规律点拨
本题考查了反比例函数的图像和性质,矩形的性质,以及利用间接法求四边形的面积,解题的关键是熟练掌握反比例函数的性质进行解题.
巩固练习
1.(2018·全国初三单元测试)如图,两个反比例函数y=和y=在第一象限内的图象分别是C1和C2,设点P(1,4)在C1上,PA⊥x轴于点A,交C2于点B(1,m),求k,m的值及△POB的面积.
【答案】k=4,m=2,.
【解析】解:∵P(1,4),∴k=4;
∵B(1,m),C2解析式为:y=,∴m=2;
S△POB=S△POA-S△BOA=2-1=1.
2.(2020·四川双流·初三其他)如图,在平面直角坐标系中,正比例函数y=x的图像与反比例函数y=的图像交于A,B两点,且点A的坐标为(6,a).
(1)求反比例函数的表达式;
(2)已知点C(b,4)在反比例函数y=的图像上,点P在x轴上,若△AOC的面积等于△AOP的面积的两倍,请求出点P的坐标.
【答案】(1)反比例函数的表达式为y=;(2)点P的坐标为(,0)或(-,0).
【解析】解:(1)∵点A(6,a)在正比例函数y=x的图像上
∴a=×6=2
∵点A(6,2)在反比例函数y=的图像上
∴2=,
k=12
∴反比例函数的表达式为y=.
(2)分别过点C,A作CD⊥轴,AE⊥轴,垂足分别为点D,E.
∵点C(b,4)在反比例函数y=的图像上
∴4=,b=3,即点C的坐标为(3,4)
∵点A,C都在反比例函数y=的图像上
∴S△OAE=S△COD=×12=6
∴S△AOC=S四边形COEA-S△OAE=S四边形COEA-S△COD=S梯形CDEA
∴S△AOC=×(CD+AE)·DE=×(4+2)×(6-3)=9
∵△AOC的面积等于△AOP的面积的两倍
∴S△AOP=S△AOC=,
设点P的坐标为(m,0)
则S△AOP=×2·︱m︱=,.
∴m=,
∴点P的坐标为(,0)或(-,0).
2.(2020·河南西华·初三一模)小亮在研究矩形的面积S与矩形的边长x,y之间的关系时,得到下表数据:
x
0.5
1
1.5
2
3
4
6
12
y
12
6
■
3
2
1.5
1
0.5
结果发现一个数据被墨水涂黑了.
(1)被墨水涂黑的数据为_________;
(2)y与x的函数关系式为_________,且y随x的增大而_________;
(3)如图是小亮画出的y关于x的函数图象,点B、E均在该函数的图象上,其中矩形的面积记为,矩形的面积记为,请判断与的大小关系,并说明理由;
(4)在(3)的条件下,交于点G,反比例函数的图象经过点G交于点H,连接、,则四边形的面积为_________.
【答案】(1)4;(2)y=,减小;(3),说明见解析;(4)4
【解析】(1)∵表格中x、y表示矩形的边长
则S=xy=0.5,解得:S=6
∴当x=1.5时,y=4;
(2)∵S=xy=6
∴y=
根据反比例函数的性质,在第一象限内,y随x的增大而减小;
(3)∵y=
其中k=6表示任取函数图像上一点P,过点分别做x轴、y轴垂线,则与坐标轴构成的矩形面积为6
∴,
∴;
(4)如下图,ED与OH交于点M
反比例函数k的几何意义还可以如下图,表示为:任取函数上一点P,向x轴作垂线,交x轴于点N,则△ONP的面积为
∵点G在函数图像上
∴==1
∴
∴.
3.如图,点在双曲线的第一象限的那一支上,垂直于轴于点,点在轴正半轴上,且,点在线段上,且,点为的中点,若的面积为3,则的值为______.
【答案】
【解析】解:连接DC,如图,
∵AE=3EC,△ADE的面积为3,
∴△CDE的面积为1,
∴△ADC的面积为4,
设A点坐标为(a,b),则AB=a,OC=2AB=2a,
而点D为OB的中点,
∴BD=OD=b,
∵S梯形OBAC=S△ABD+S△ADC+S△ODC,
∴(a+2a)×b=a×b+4+×2a×b,
∴ab=,
把A(a,b)代入双曲线y=,
∴k=ab=.
故答案为:.
4.(2019·石家庄市第十七中学初三期中)如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
【答案】(1);(2).
【解析】解:(1)∵反比例函数y=在第一象限内,
∴k>0,
∵S△BOD=k,
∴k=4,
解得k=8,
∴反比例函数解析式为;
(2)当A点恰好移到上时,
∵AB=8,即为点A的纵坐标的值,
∴点A的横坐标是:,
∵OB=4,
∴点A移动的距离是4-1=3,移动的时间是3÷3=1秒,
所以若△AOB与反比例函数图象没有交点,则.
5.(2019·河北桥东·邢台三中初三月考)已知反比例函数y=的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
【答案】(1)第三象限,m>2;(2)m=8
【解析】解(1)根据反比例函数的图象关于原点对称知,该函数图象的另一支在第三象限,且m﹣2>0,则m>2;
(2)∵点B与点A关于x轴对称,若△OAB的面积为6,设AB交x轴于点C,
∴△OAC的面积为3.
设A(x, ),
则:△OAC的面积•=3,
解得m=8.
6.(2019·河北保定·初三期末)如图所示,点A(,3)在双曲线y=上,点B在双曲线y=之上,且AB∥x轴,C,D在x轴上,若四边形ABCD为矩形,求它的面积.
【答案】2
【解析】解:∵A(,3),AB∥x轴,点B在双曲线y=之上,
∴B(1,3),
∴AB=1﹣=,AD=3,
∴S=AB•AD=×3=2.
7.(2019·甘肃天水·初三期中)如图所示,双曲线经过斜边上的点,且满足,与交于点,,求的值.
【答案】8
【解析】过作轴,垂足为,则
∵
∴
∴
∵
∴
∴
∵点,分别在双曲线上,
∴.
∴
∴
∴
8.(2018·全国初三单元测试)如图.矩形的边,在坐标轴上,顶点在第一象限,反比例函数的图象经过的中点,交于点,且四边形的面积为.求的值.
【答案】
【解析】解:设点坐标为,
∵矩形的边的中点为,
∴点的坐标为,
∴,
∴,
∵矩形,
∴,
∴,
∴.
9.(2019·全国初三单元测试)如图,若点在反比例函数的图象上,轴于点,的面积为.
求的值;
当点在反比例函数图象上运动,其它条件不变,的面积发生变化吗?并说明你的理由.
【答案】(1);(2)的面积不发生变化.
【解析】解:∵的面积是,
∴.
又∵图象在二,四象限,,
∴.
∵是反比例函数图象上的点,
∴,
∴的面积不发生变化.
10.(2018·全国初三期末)已知反比例函数的图象如图所示,点,是该图象上的两点.
(1)求的取值范围;
(2)比较与的大小;
(3)若点在该反比例函数图象上,求此反比例函数的解析式;
(4)若为第一象限上的一点,作轴于点,求的面积(用含的式子表示)
【答案】(1);(2);(3):;(4).
【解析】(1)∵反比例函数的图象在一、三象限,
,即;
(2)∵反比例函数的图象在一、三象限,
∴在每一象限内随的增大而减小,
∴,
∴;
(3)∵点在该反比例函数图象上,
∴,解得,
∴此函数的解析式为:;
(4)∵为第一象限上的一点,轴于点,
∴.
11. (2020·大石桥市周家镇中学初三月考)已知反比例函数y=(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D
(1)求这个反比函数的表达式;
(2)求△ACD的面积.
【答案】(1 );(2)6.
【解析】(1)将B点坐标代入y=中,得=2,解得k=6,
∴反比例函数的解析式为y=.
(2)∵点B与点C关于原点O对称,
∴C点坐标为(-3,-2).
∵BA⊥x轴,CD⊥x轴,
∴A点坐标为(3,0),D点坐标为(-3,0).
∴S△ACD=AD·CD=×[3-(-3)]×|-2|=6
初中人教版26.1.1 反比例函数课后作业题: 这是一份初中人教版26.1.1 反比例函数课后作业题,共23页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
人教版九年级下册29.1 投影课时作业: 这是一份人教版九年级下册29.1 投影课时作业,共48页。试卷主要包含了知识点,考点点拨与训练等内容,欢迎下载使用。
初中数学人教版九年级下册26.2 实际问题与反比例函数同步测试题: 这是一份初中数学人教版九年级下册26.2 实际问题与反比例函数同步测试题,共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。