人教版八年级下册18.1.1 平行四边形的性质示范课ppt课件

这是一份人教版八年级下册18.1.1 平行四边形的性质示范课ppt课件，共21页。PPT课件主要包含了情景引入，记作ABCD，知识点1，知识点2，跟踪训练1，跟踪训练2，拼一拼，测量法，平移法，如何证明等内容，欢迎下载使用。
1.理解并掌握平行四边形的概念及掌握平行四边形的定 义和对边相等、对角相等的两条性质.（重点）2.根据平行四边形的性质进行简单的计算和证明.（难点） 3.经历“实验—猜想—验证—证明”的过程,发展学生的 思维水平.
你还能举出其他的例子吗？
问题1 你知道什么样的图形叫做平行四边形吗？
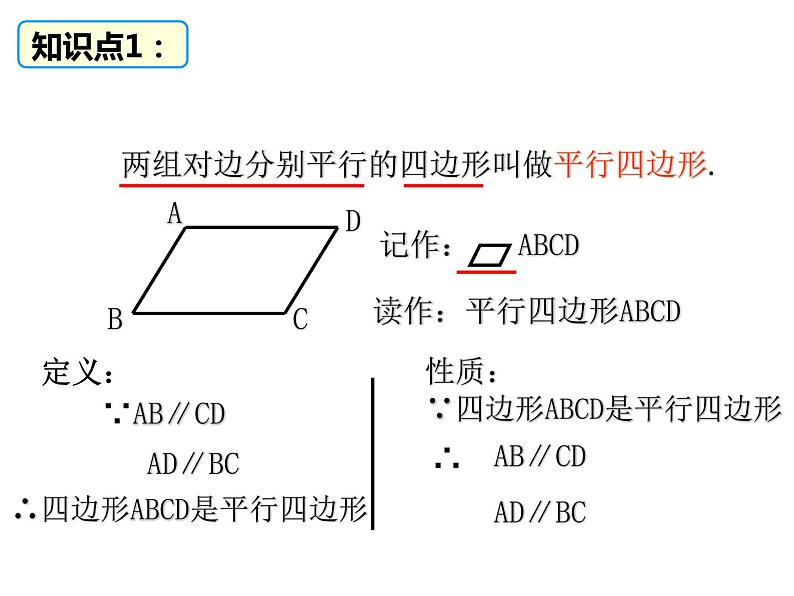
两组对边分别平行的四边形叫做平行四边形.
读作：平行四边形ABCD
∴四边形ABCD是平行四边形
性质：∵四边形ABCD是平行四边形
1.定义：两组对边分别平行的四边形叫做平行四边形.
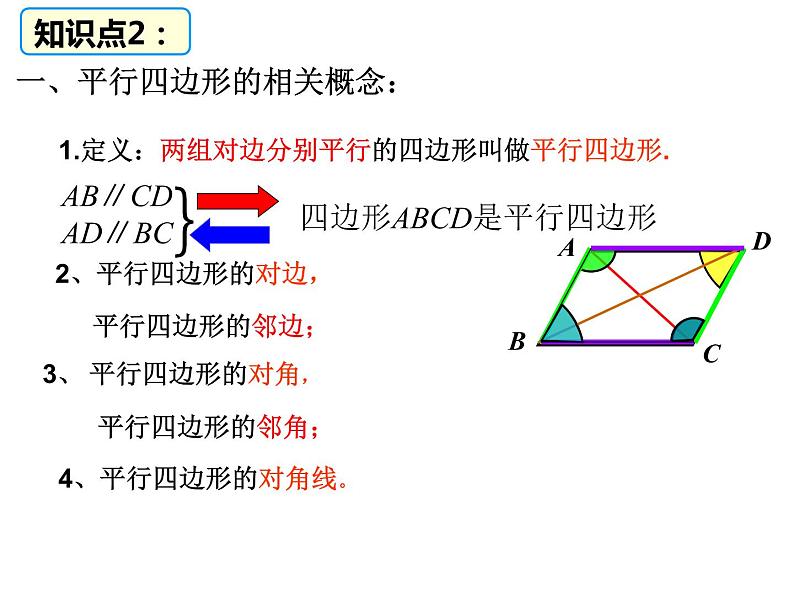
4、平行四边形的对角线。
四边形ABCD是平行四边形
一、平行四边形的相关概念：
3、 平行四边形的对角，
2、平行四边形的对边，
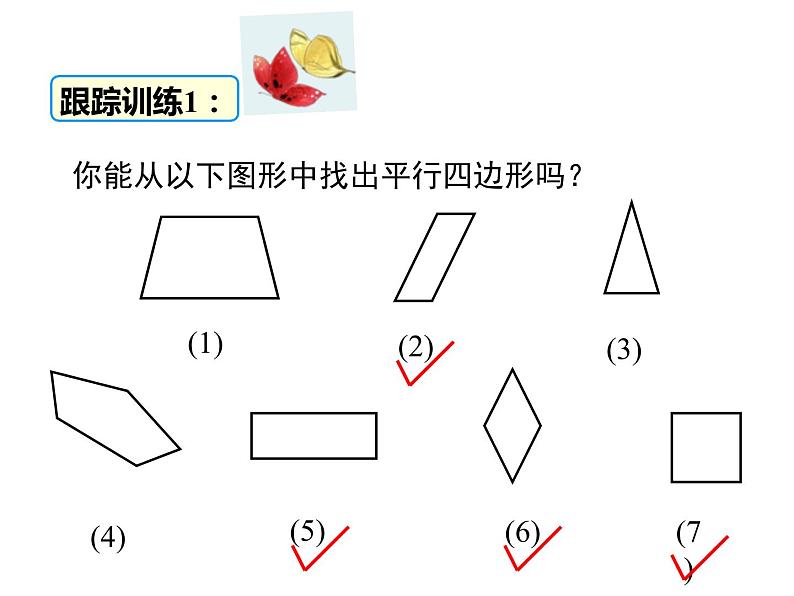
你能从以下图形中找出平行四边形吗？
如图，AB∥DC，EF∥ DC,AD∥ BC，图中的平行四边形有多少个？将它们表示出来，并说明理由。
理由：∵AB∥DC，AD∥ BC ∴四边形ABCD是平行四边形.同理可得：四边形ABFE是平行四边形；四边形CDEF是平行四边形.
解：图中有3个平行四边形：ABCD, ABFE, CDEF.
请你用手中一对全等的三角形纸片拼出平行四边形，能拼出几种不同的平行四边形呢？　　　　　　　　
从拼图可以得到什么启示？
小结： 平行四边形可以是由两个全等的三角形组成，因此在解决平行四边形的问题时，通常可以连结对角线转化为两个全等的三角形进行解题。
观察平行四边形，边与边、角与角之间还有什么关系？并验证你的猜想。
平行四边形的对边相等；平行四边形的对角相等.
平行四边形的对边相等；平行四边形的对角相等.
平行四边形的对边平行、相等；
平行四边形的对边相等，对角相等。
已知：四边形ABCD是平行四边形.求证：AB=CD,AD=BC ∠A= ∠C, ∠B= ∠D.
提示：可连接BD，试证△______≌△______
1.在 ABCD中，若∠B=70°，则∠D=（ ）. A.130° B.110° C.70° D.35°
2.在 ABCD中，若AB=2，BC=3，则 ABCD的周长是____。
方法1：证明： ∵四边形ABCD是平行四边形，∴ ∠A= ∠C，AD=CB.又∠AED= ∠CFB=90°，∴ △ADE≌△CBF（AAS）,∴AE=CF.
方法2：证明：∵四边形ABCD是平行四边形，∴AB=CD AB∥CD 即DF∥BE∵DE⊥AB，BF⊥CD，垂足分别是E，F．∴DE∥BF∴四边形DEBF是平行四边形∴DF=BE∵AB-BE=CD-DF即AE=CF
【小结】：证明线段相等，除了运用全等三角形的性质，还可以利用平行四边形的性质得到。
有一块形状如图 所示的玻璃，不小心把EDF部分打碎了，现在只测得AE=60cm，BC=80cm，∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗？
解：∵AE//BC，AB//CF，
∴四边形ABCD是平行四边形.
∴∠D=∠B=60°，AD=BC=80cm.
∴DE=AD-AE=20cm.
答：DE的长度是20cm, ∠D的度数是60°.
在本节课的学习中有哪些收获？与你的同伴进行交流．1.平行四边形的定义、性质： 边：平行四边形的对边平行且相等； 角：平行四边形的对角相等；邻角互补；2.对于平行四边形，你觉得还需要进一步研究什么？