人教版新课标A必修43.1 两角和与差的正弦、余弦和正切公式示范课课件ppt

这是一份人教版新课标A必修43.1 两角和与差的正弦、余弦和正切公式示范课课件ppt，文件包含313ppt、313doc等2份课件配套教学资源，其中PPT共37页， 欢迎下载使用。
3.1　两角和与差的正弦、余弦和正切公式
3.1.3　二倍角的正弦、余弦、正切公式
在我们接触到的事物中，带有一般性的事物总是大开大合，纵横驰骋，往往包含一切，而特殊的事物则是小巧玲珑，温婉和融，往往显出简洁，奇峻之美．三角函数的和(差)角的正弦、余弦、正切公式中的角都是带有一般性的，一般性中又蕴含着特殊性，即两角相等的情形，那么这些二倍角又有什么简洁，奇峻之美呢？
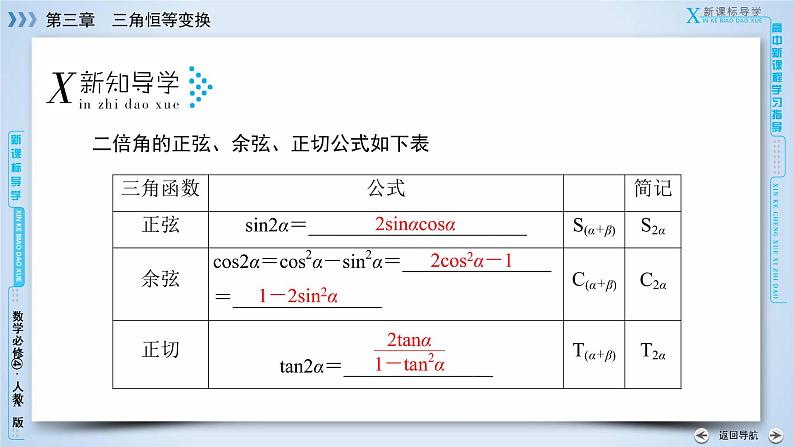
二倍角的正弦、余弦、正切公式如下表
1．判断下列说法是否正确，正确的在后面的括号内打“√”，错误的打“×”．(1)对任意的角总有sin2θ＝2sinθ.(　　)(2)不存在角α，使得cs2θ＝2csθ.(　　)
命题方向1　⇨利用二倍角公式解决给角求值问题
『规律总结』　对于给角求值问题，一般有两类：(1)直接正用、逆用二倍角公式，结合诱导公式和同角三角函数的基本关系对已知式进行转化，一般可以化为特殊角．(2)若形式为几个非特殊角的三角函数式相乘，则一般逆用二倍角的正弦公式，在求解过程中，需利用互余关系配凑出应用二倍角公式的条件，使得问题出现可以连用二倍角的正弦公式的形式．
二倍角公式的变形应用
[误区警示]　盲目地运用公式化简函数的解析式，而忽略定义域，是解决与三角函数有关问题的易错点，要想正确求解，需要掌握倍角、分角的终边所在象限的确定方法，这在第一章中已经详细介绍，此处不再赘述．