2021年北京朝阳区脉露第三中学八年级下期末数学试卷

这是一份2021年北京朝阳区脉露第三中学八年级下期末数学试卷，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共10小题；共50分）
1. 如图，紫荆花图案绕中心至少旋转 x∘ 后能与原来的图案互相重合，则 x 的值为
A. 36B. 45C. 60D. 72

2. 以下列线段的长为三边的三角形中，能构成直角三角形的是
A. 32，42，52B. 13，5，12C. 13，14，15D. 312，412，512

3. 在平行四边形 ABCD 中，如果 ∠A+∠C=140∘，那么 ∠C 等于
A. 70∘B. 60∘C. 40∘D. 20∘

4. 八年级（3）班同学要在广场上布置一个矩形的花坛，如图，计划用红花摆成两条对角线．如果一条对角线用了 49 盆红花，那么还需要从花房运来红花
A. 48 盆B. 49 盆C. 50 盆D. 51 盆

5. 已知一个函数的因变量 y 与自变量 x 的部分对应值满足下表：
x4321−1−2−3−4y1.5236−6−3−2−1.5
则这个函数的关系式为
A. y=6xB. y=x6C. y=−6xD. y=x5

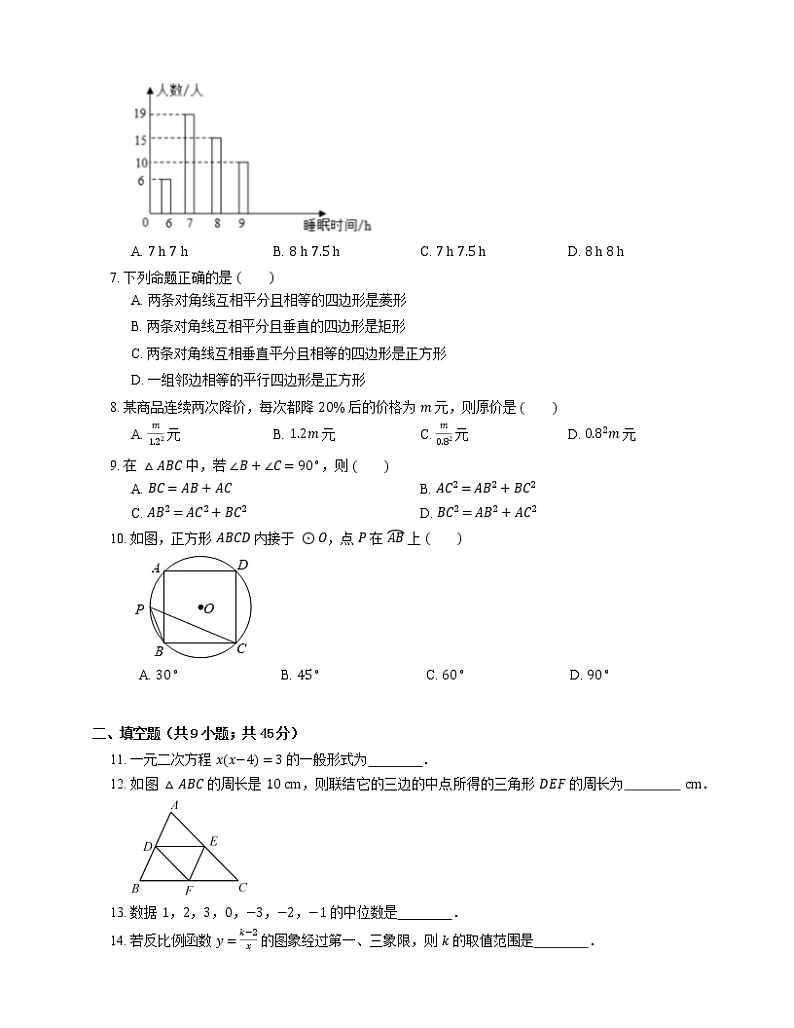
6. 为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，调查了一个班 50 名学生每天的睡眠时间，绘成睡眠时间频数分布直方图如图所示，则所调查学生睡眠时间的众数，中位数分别为
A. 7 h 7 hB. 8 h 7.5 hC. 7 h 7.5 hD. 8 h 8 h

7. 下列命题正确的是
A. 两条对角线互相平分且相等的四边形是菱形
B. 两条对角线互相平分且垂直的四边形是矩形
C. 两条对角线互相垂直平分且相等的四边形是正方形
D. 一组邻边相等的平行四边形是正方形

8. 某商品连续两次降价，每次都降 20% 后的价格为 m 元，则原价是
A. m1.22 元B. 1.2m 元C. m0.82 元D. 0.82m 元

9. 在 △ABC 中，若 ∠B+∠C=90∘，则
A. BC=AB+ACB. AC2=AB2+BC2
C. AB2=AC2+BC2D. BC2=AB2+AC2

10. 如图，正方形 ABCD 内接于 ⊙O，点 P 在 AB 上
A. 30∘B. 45∘C. 60∘D. 90∘

二、填空题（共9小题；共45分）
11. 一元二次方程 xx−4=3 的一般形式为 ．

12. 如图 △ABC 的周长是 10 cm，则联结它的三边的中点所得的三角形 DEF 的周长为 cm．

13. 数据 1，2，3，0，−3，−2，−1 的中位数是 ．

14. 若反比例函数 y=k−2x 的图象经过第一、三象限，则 k 的取值范围是 ．

15. 已知一个平行四边形两个内角的度数比为 1:3，则其中较小的内角为 ．

16. 将代数式 x2+6x+7 进行如下变形：x2+6x+7=x2+2⋅x⋅3+9−9+7=x+32−2，当 x 的值为 时，x+32 的最小值为 0，即 x+32−2 的最小值为 −2，从而代数式 x2+6x+7 的最小值为 ．

17. 如图，在平行四边形 ABCD 中，AE⊥BC 于点 E，AF⊥CD 于点 F，若 ∠EAF=58∘，则 ∠BAD= ．

18. 以菱形 ABCD 的对角线交点 O 为原点，对角线 AC，BD 所在直线为坐标轴，建立如图所示的直角坐标系，AD 的中点 E 的坐标为 −1,2，则 BC 的中点 F 的坐标为 ．

19. 七巧板是我们祖先的一项卓越创造，被誉为“东方魔板”，小明利用七巧板（如图①所示）中各板块的边长之间的关系拼成一个凸六边形（如图②所示），则该凸六边形的周长是 cm．

三、解答题（共9小题；共117分）
20. 解下列方程：
（1）x2−2x−1=0；
（2）x+32=4x−32．

21. 如图，在平行四边形 ABCD 中，E 为 BC 上的一点，连接 AE，BD，且 AE=AB．
（1）求证：∠ABE=∠EAD．
（2）若 ∠AEB=2∠ADB，求证：四边形 ABCD 是菱形．

22. 如图，△ABC 的三个顶点都在边长为 1 的小正方形组成的网格的格点上，以点 O 为原点建立平面直角坐标系，回答下列问题：
（1）将 △ABC 绕原点 O 旋转 180∘ 得到 △A1B1C1，在表格中画出 △A1B1C1；
（2）已知点 A 的坐标为 −4,−1，则点 A1 的坐标为 ．

23. 为了解某地区中学生一周课外阅读时长的情况，随机抽取部分中学生进行调查，根据调查结果，将阅读时长分为四类：2 小时以内，2∼4 小时（含 2 小时），4∼6 小时（含 4 小时），6 小时及以上，并绘制了如图所示尚不完整的统计图．
（1）本次调查共随机抽取了 名中学生，其中课外阅读时长“2∼4 小时”的有 人．
（2）扇形统计图中，课外阅读时长“4∼6 小时”对应的圆心角度数为 ∘．
（3）若该地区共有 20000 名中学生，估计该地区中学生一周课外阅读时长不少于 4 小时的人数．

24. 已知关于 x 的一元二次方程 x2+k+1x+k=0．
（1）求证：方程总有两个实数根；
（2）若该方程有一个根是正数，求 k 的取值范围．

25. （1）如图 1，在正方形 ABCD 的边 CD 上任取一点 E，作 EF⊥CD，交 CH 于点 F，取 AF 的中点 H，连接 EH，BH．判断线段 EH 和 BH 有怎样的数量关系和位置关系?并加以证明；
（2）若将图 1 中的 △CEF 绕点 C 顺时针旋转 90 度，如图 2，判断线段 EH 和 BH 有怎样的数量关系和位置关系?不写证明，直接写出结论；
（3）若将图 1 中的 △CEF 绕点 C 顺时针旋转 180 度，如图 3，判断线段 EH 和 BH 有怎样的数量关系和位置关系?并加以证明；

26. 阅读以下短文，然后解决下列问题：
如果一个三角形和一个矩形满足条件：三角形的一边与矩形的一边重合，且三角形的这边所对的顶点在矩形这边的对边上，则称这样的矩形为三角形的“友好矩形”，如图①所示，矩形 ABEF 即为 △ABC 的“友好矩形”，显然，当 △ABC 是钝角三角形时，其“友好矩形”只有一个．
（1）仿照以上叙述，说明什么是一个三角形的“友好平行四边形”；
（2）若 △ABC 为直角三角形，且 ∠C=90∘，在图②中画出 △ABC 的所有“友好矩形”，并比较这些矩形面积的大小；
（3）若 △ABC 是锐角三角形，且 BC>AC>AB，在图③中画出 △ABC 的所有“友好矩形”，指出其中周长最小的矩形并加以证明．

27. 如图，Rt△ABC 的斜边 AC 的两个顶点在反比例函数 y=k1x 的图象上，点 B 在反比例函数 y=k2x 的图象上，AB 与 x 轴平行，BC=2，点 A 的坐标为 1,3．
（1）求 C 点的坐标．
（2）求点 B 所在函数图象的解析式．

28. 已知：如图，在矩形 ABCD 中，E 是 BC 边一点，DE 平分 ∠ADC，EF∥DC 交 AD 边于点 F，连接 BD．
（1）求证：四边形 EFCD 是正方形．
（2）若 BE=1，ED=22，求 BD 的长．
答案
第一部分
1. D
2. B【解析】A．322+422≠522，不能构成直角三角形；
B．52+122=132，能构成直角三角形；
C．142+152≠132，不能构成直角三角形；
D．3122+4122≠5122，不能构成直角三角形．故选B．
3. A
4. A【解析】∵ 矩形的对角线互相平分且相等，
∴ 一条对角线用了 49 盆红花，中间一盆为对角线交点，
∴ 还需要从花房运来红花 49−1=48 盆．
5. A
【解析】由题中表格可知 x 与 y 的乘积等于 6，所以这个函数的关系式为 y=6x．
6. C【解析】∵7 h 出现了 19 次，出现的次数最多，
∴ 所调查学生睡眠时间的众数是 7 h；
∵ 共有 50 名学生，中位数是第 25，26 个数的平均数，
∴ 所调查学生睡眠时间的中位数是 7+82=7.5h．
7. C【解析】选项A 两条对角线互相平分且相等的四边形是矩形，故错误；
选项B 两条对角线互相平分且垂直的四边形是菱形，故错误；
选项C 两条对角线互相垂直平分且相等的四边形是正方形，正确；
选项D 一组邻边相等的平行四边形是菱形，故错误．
8. C
9. D【解析】∵ 在 △ABC 中，若 ∠B+∠C=90∘，
∴∠A=90∘，
∴BC2=AB2+AC2，
故选：D．
10. B
【解析】连接 OB，OC，
∵ 正方形 ABCD 内接于 ⊙O，
∴BC 弧所对的圆心角为 90∘，
∴∠BOC=90∘，
∴∠BPC=12∠BOC=45∘．
第二部分
11. x2−4x−3=0
12. 5
【解析】根据 D，E 分别是 AB 和 AC 的中点，得到 DE∥BC，并且 BC=2DE．
同理，根据 E，F 分别是 AC 和 BC 的中点，得到 EF∥AB，并且 AB=2EF．
根据 D，F 分别是 AB 和 BC 的中点，得到 DF∥AC，并且 AC=2DF．
所以，三角形 DEF 的周长 =DE+EF+FD=12BC+AB+AC=5 cm．
13. 0
14. k>2
15. 45∘
16. −3，−2
17. 122∘
【解析】因为 AE⊥BC 于点 E，AF⊥CD 于点 F，
所以 ∠AEC=∠AFC=90∘，
又因为 ∠EAF=58∘，
所以 ∠C=360∘−58∘−90∘−90∘=122∘，
因为四边形 ABCD 是平行四边形，
所以 ∠BAD=∠C=122∘．
18. 1,−2
【解析】因为 AD 的中点 E 的坐标为 −1,2，
所以 A−2,0，D0,4，
因为四边形 ABCD 是菱形，
所以 OB=OD，OA=OC，
所以 B0,−4，C2,0，
所以 BC 的中点 F 的坐标为 1,−2．
19. 322+16
第三部分
20. （1）
∵a=1,b=−2,c=−1.∴Δ=−22−4×1×−1=8>0.
则
x=2±222=1±2.
（2）
∵x+32=4x−32.∴x+3=2x−3或x+3=−2x−3.
解得
x=9或x=1.
21. （1） 在平行四边形 ABCD 中，
∵AD∥BC，
∴∠AEB=∠EAD，
∵AE=AB，
∴∠ABE=∠AEB，
∴∠ABE=∠EAD．
（2） ∵AD∥BC，
∴∠ADB=∠DBE，
∵AE=AB，
∴∠ABE=∠AEB，∠AEB=2∠ADB，
∴∠ABE=2∠ADB，
∴∠ABD=∠ABE−∠DBE=2∠ADB−∠ADB=∠ADB，
∴AB=AD，
又 ∵ 四边形 ABCD 是平行四边形，
∴ 四边形 ABCD 是菱形．
22. （1） 如图，△A1B1C1 即为所求．
（2） 4,1
23. （1） 200；40
【解析】本次调查共随机抽取了：50÷25%=200（名）中学生，
其中课外阅读时长“2∼4 小时”的有：200×20%=40（人），
故答案为：200；40．
（2） 144
【解析】扇形统计图中，课外阅读时长“4∼6 小时”对应的圆心角度数为：360∘×1−30200−20%−25%=144∘，
故答案为：144．
（3） 20000×1−30200−20%=13000（人），
答：该地区中学生一周课外阅读时长不少于 4 小时的有 13000 人．
24. （1） 依题意，得 Δ=k+12−4k=k−12．
∵k−12≥0，
∴ 方程总有两个实数根．
（2） 由求根公式，得 x1=−1，x2=−k．
∵ 方程有一个根是正数，
∴−k>0，
∴k<0．
25. （1） EH=BH，EH⊥BH，理由如下：
延长 EF 交 AB 于点 G，并连接 HG．
在正方形 ABCD 中，EF⊥CD，即 EG⊥AB．
易知三角形 △AGF，△CEF 为等腰直角三角形，
四边形 CEGB 为矩形．
∵ 点 H 为 AF 的中点
∴GH=12AF=HF．
在等腰直角三角形 △AGF 中，点 H 为 AF 的中点，∠HGF=∠GFH=45∘，∠GHF=90∘，
∴∠HGB=∠HFE=135∘，
在等腰直角三角形 △CEF 和矩形 CEGB 中，GB=EC=EF，
∴△HGB≌△HFE .
∴BH=EH，∠GHB=∠FHE．
又 ∠GHF=90∘，即 ∠GHB+∠BHF=90∘，
∴∠EHF+∠BHF=90∘，即 BH⊥EH．
（2） EH=BH，EH⊥BH．
【解析】过 F 作 FG⊥AB 垂足为 G 交 CD 于 N，连接 AC，GH，CH .
∵△CEF 绕点 C 顺时针旋转 90 度，
∴B 、 C，E 共线．
∵∠ACD=45∘ ，
∴∠ACF=90∘ .
∵H 为 AF 中点，
∴CH=HF .
∵CE=EF，HE=HE ，
∴△HCE≌△HFE .
∴HE 平分 ∠CEF .
∴HE 与 CD 的交点为 N .
∵FG⊥AB，H 为 AF 中点，
∴GH=HF，GB=EF .
∴∠HGF=∠HFG .
∴∠HGB=∠HFE .
∴△HGB≌△HFE .
∴HB=HE，∠GBH=∠FEH=45∘ .
∵∠HEB=45∘ ，
∴HB⊥HE .
（3） EH=BH，EH⊥BH．理由如下：
延长 FE 交 AB 的延长线于点 G，并连接 HG．
在正方形 ABCD 中，EF⊥CD，即 FG⊥AB．
易知三角形 △AGF，△CEF 为等腰直角三角形，
四边形 CEGB 为矩形．
∵ 点 H 为 AF 的中点，
∴GH=12AF=HF．
在等腰直角三角形 △AGF 中，点 H 为 AF 的中点，
∠HGA=∠F=45∘，∠GHF=90∘．
在等腰直角三角形 △CEF 和矩形 CEGB 中，GB=EC=EF，
∴△HGB≌△HFE，
∴BH=EH，∠GHB=∠FHE．
又 ∠GHF=90∘，即 ∠FHE+∠EHG=90∘，
∴∠EHG+∠GHB=90∘，即 BH⊥EH．
26. （1） 如果一个三角形和一个平行四边形满足条件：三角形的一边与平行四边形的一边重合，且三角形的这边所对的顶点在平行四边形这边的对边上，则称这样的平行四边形为三角形的“友好平行四边形”．
（2） 如图，
此时共有 2 个“友好矩形”，矩形 BCAD 和矩形 ABEF．
易知矩形 BCAD 和矩形 ABEF 的面积都等于 △ABC 面积的 2 倍，
∴△ABC 的“友好矩形”的面积相等．
（3） 如图，
此时共有 3 个“友好矩形”，矩形 BCDE 、矩形 CAFG 及矩形 ABHK，其中矩形 ABHK 的周长最小．
证明：易知这三个矩形的面积相等，令其为 S，
设矩形 BCDE 、矩形 CAFG 及矩形 ABHK 的周长分别为 L1，L2，L3，△ABC 中 BC=a，CA=b，AB=c，
则 L1=2Sa+2a，L2=2Sb+2b，L3=2Sc+2c，
∴L1−L2=2Sa+2a−2Sb+2b=−2Saba−b+2a−b=2a−bab−Sab，易知 ab>S，且 a>b，
∴L1−L2>0，即 L1>L2，同理可得，L2>L3，
∴L3 最小，即矩形 ABHK 的周长最小．
27. （1） 把点 A1,3 代入反比例函数 y=k1x 得 k1=1×3=3，
∴ 过 A 点与 C 点的反比例函数解析式为 y=3x，
∵AB 与 x 轴平行，
∴B 点的纵坐标为 3，
∵BC 平行 y 轴，BC=2，
∴C 点的纵坐标为 1，
把 y=1 代入 y=3x 得 x=3，
∴C 点坐标为 3,1．
（2） 把 B3,3 代入反比例函数 y=k2x 得 k2=3×3=9，
∴ 点 B 所在函数图象的解析式为 y=9x．
28. （1） ∵ 四边形 ABCD 是矩形，
∴AD∥BC，∠ADC=∠C=90∘，
∵EF∥DC，
∴ 四边形 FECD 为平行四边形，
∵DE 平分 ∠ADC，
∴∠ADE=∠CDE，
∴AD∥BC，
∴∠ADE=∠DEC，
∴∠CDE=∠DEC，
∴CD=CE，
∴ 四边形 FECD 是菱形，
又 ∵∠C=90∘，
∴ 平行四边形 FECD 是正方形．
（2） ∵ 四边形 FECD 是正方形，
∴∠CDE=45∘，
∵ED=22，
∴CE=CD=ED⋅sin45∘=22×22=2，
∴BC=BE+EC=1+2=3，
∴BD2=BC2+CD2=32+22=13，
∴BD=13．