2021年北京房山区晨曦学校八年级上期末数学试卷

这是一份2021年北京房山区晨曦学校八年级上期末数学试卷，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题（共8小题；共40分）
1. 下列方程中，关于 x 的一元二次方程是
A. 3x+12=2x+1B. 1x2+1x−2=0
C. ax2+bx+c=0D. x2+2x=x2−1

2. 用以下各组线段为边，可以组成三角形的是
A. 2 cm，4 cm，6 cmB. 2 cm，5 cm，7 cm
C. 2 cm，5 cm，8 cmD. 4 cm，5 cm，8 cm

3. 若分式 ∣x∣−1x+1 的值为零，则 x 的值是
A. 1B. −1C. ±1D. 2

4. 下列二次根式中，不能与 2 合并的是
A. 12B. 8C. 12D. 18

5. 下列等式从左到右变形正确的是
A. yx=y+1x+1B. yx=ayaxC. yx=a2ya2xD. yx=a2+1ya2+1x

6. 若一个数的立方根是 −3，则该数为
A. −33B. −27C. ±33D. ±27

7. 知识改变世界，科技改变生活，导航装备的不断更新极大方便了人们的出行．周末，小强一家到 B，C 两处景区游玩，他们从家 A 处出发，向正北行驶 160 km 到达 B 处，若在 A 处测得景区 C 在北偏西 34∘ 方向上，且 ∠ACB=32∠BAC，则在 B 处测得景区 C 应位于
A. 北偏西 68∘B. 南偏西 85∘C. 北偏西 85∘D. 南偏西 68∘

8. 观察如图图形，照此规律，第 5 个图形中白色三角形的个数是
A. 81B. 121C. 161D. 201

二、填空题（共8小题；共40分）
9. 9 意义，0 意义，−9 意义．（填“有”或“无”）

10. 若关于 x 的方程 x2+ax−2=0 有一个根是 1，则 a= ．

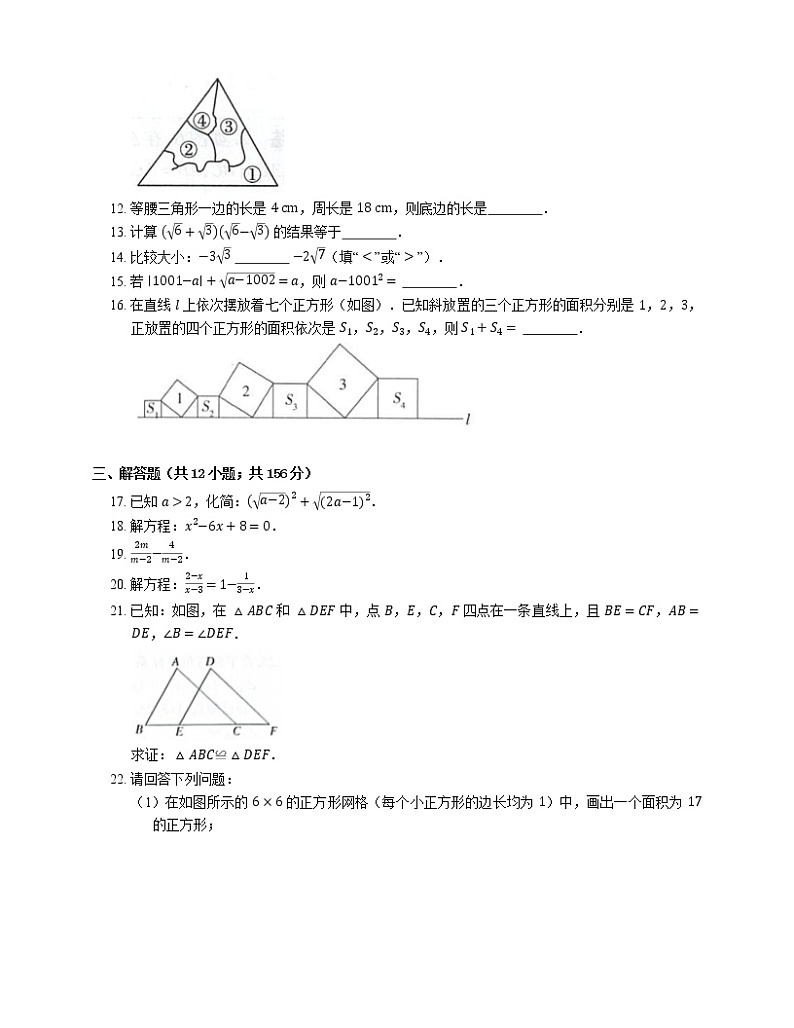
11. 如图，某同学把一块三角形的玻璃打碎成了四块，现在要到玻璃店配一块完全一样的玻璃，则他需要带 去．（填序号）

12. 等腰三角形一边的长是 4 cm，周长是 18 cm，则底边的长是 ．

13. 计算 6+36−3 的结果等于 ．

14. 比较大小：−33 −27（填“<”或“>”）．

15. 若 1001−a+a−1002=a，则 a−10012= ．

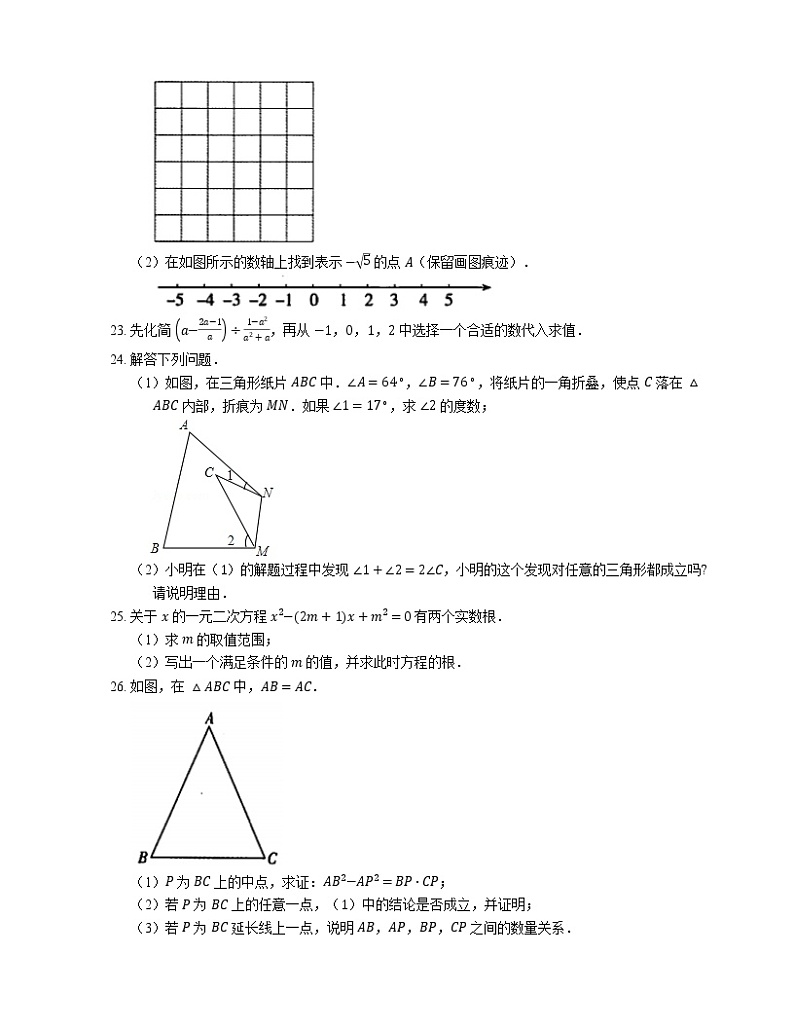
16. 在直线 l 上依次摆放着七个正方形（如图）．已知斜放置的三个正方形的面积分别是 1，2，3，正放置的四个正方形的面积依次是 S1，S2，S3，S4，则 S1+S4= ．

三、解答题（共12小题；共156分）
17. 已知 a>2，化简：a−22+2a−12．

18. 解方程：x2−6x+8=0．

19. 2mm−2−4m−2．

20. 解方程：2−xx−3=1−13−x．

21. 已知：如图，在 △ABC 和 △DEF 中，点 B，E，C，F 四点在一条直线上，且 BE=CF，AB=DE，∠B=∠DEF．
求证：△ABC≌△DEF．

22. 请回答下列问题：
（1）在如图所示的 6×6 的正方形网格（每个小正方形的边长均为 1）中，画出一个面积为 17 的正方形；
（2）在如图所示的数轴上找到表示 −5 的点 A（保留画图痕迹）．

23. 先化简 a−2a−1a÷1−a2a2+a，再从 −1，0，1，2 中选择一个合适的数代入求值．

24. 解答下列问题．
（1）如图，在三角形纸片 ABC 中．∠A=64∘，∠B=76∘，将纸片的一角折叠，使点 C 落在 △ABC 内部，折痕为 MN．如果 ∠1=17∘，求 ∠2 的度数；
（2）小明在（1）的解题过程中发现 ∠1+∠2=2∠C，小明的这个发现对任意的三角形都成立吗?请说明理由．

25. 关于 x 的一元二次方程 x2−2m+1x+m2=0 有两个实数根．
（1）求 m 的取值范围；
（2）写出一个满足条件的 m 的值，并求此时方程的根．

26. 如图，在 △ABC 中，AB=AC．
（1）P 为 BC 上的中点，求证：AB2−AP2=BP⋅CP；
（2）若 P 为 BC 上的任意一点，（1）中的结论是否成立，并证明；
（3）若 P 为 BC 延长线上一点，说明 AB，AP，BP，CP 之间的数量关系．

27. 如图，某公司会计欲查询乙商品的进价，发现进货单已被墨水污染．
商品采购员李阿姨和仓库保管员王师傅对采购情况回忆如下：
李阿姨：我记得甲商品进价比乙商品进价每件高 50%．
王师傅：甲商品比乙商品的数量多 40 件．
请你求出乙商品的进价，并帮助他们补全进货单．

28. 下面是数学课堂的一个学习片段．阅读后，请回答下面的问题：
学习等腰三角形有关内容后，张老师请同学们交流讨论这样一个问题：“已知等腰三角形 ABC 的角 A 等于 30∘，请你求出其余两角”．同学们经片刻的思考与交流后，李明同学举手讲：“其余两角是 30∘ 和 120∘”；王华同学说：“其余两角是 75∘ 和 75∘”．还有一些同学也提出了不同的看法 ⋯⋯
（1）假如你也在课堂中，你的意见如何，为什么?
（2）通过上面数学问题的讨论，你有什么感受?（用一句话表示）
答案
第一部分
1. A
2. D
3. A【解析】分式的值要为零，则分子为零，且分母不为零．
4. C
5. D
【解析】A 、分子分母加减，分式的值改变，故A错误；
B 、当 a=0 时分式无意义，故B错误；
C 、当 a=0 时分式无意义，故C错误；
D 、分式的分子分母都乘或除以同一个不为零的整式，分式的值不变，故D正确．
6. B
7. C【解析】如图，
根据题意可知 ∠A=34∘，
∵∠ACB=32∠BAC，
∴∠ACB=32×34∘=51∘．
由三角形外角的性质可知 ∠1=∠ACB+∠BAC=34∘+51∘=85∘．
故选C．
8. B【解析】∵ 第一个图形中白色三角形的个数是 1，
第二个图形中白色三角形的个数是 1+1×3=4，
第三个图形中白色三角形的个数是 1+4×3=13，
∴ 第四个图形中白色三角形的个数是 1+13×3=40，
第五个图形中白色三角形的个数是 1+40×3=121．
第二部分
9. 有，有，无
10. 1
【解析】把 x=1 代入方程得 1+a−2=0，解得 a=1．
11. ①
12. 4 cm
13. 3
14. >
15. 1002
【解析】因为 a−1002≥0，
所以 a≥1002，
由 1001−a+a−1002=a，得 −1001+a+a−1002=a，
所以 a−1002=1001，则 a−1002=10012，
所以 a−10012=1002．
16. 2
【解析】如图，
在 △CDE 和 △ABC 中，
∠EDC=∠CBA,∠ECD=∠CAB,EC=CA,
∴△CDE≌△ABCAAS，
∴AB=CD，BC=DE，
∴AB2+DE2=DE2+CD2=CE2=3，
同理可证 FG2+LK2=HL2=1，
∴S1+S2+S3+S4=HL2+CE2=1+3=4．
∵S2+S3=2，
∴S1+S4=2．
第三部分
17. 3a−3．
18.
x2−6x+8=0.x−2x−4=0.∴x−2=0 或 x−4=0.∴x1=2,x2=4.
19. 2
20. 方程两边乘 x−3，得
2−x=x−3+1.
解得
x=2.
经检验，x=2 是原分式方程的解．
21. ∵BE=CF，
∴BC=EF，
∴ 在 △ABC 与 △DEF 中，
AB=DE∠B=∠DEFBC=EF
∴△ABC≌△DEFSAS．
22. （1） 如图所示．
（2） 如图所示．
23. 原式=a2−2a+1a⋅a2+a1−a2=a−12a⋅aa+11+a1−a=1−a.
因为分母不等于 0，
所以 a 不能取 0，±1，
所以当 a=2 时，
原式=1−a=1−2=−1．
24. （1） ∵△ABC 中，∠A=64∘，∠B=76∘，
∴∠C=180∘−∠A−∠B=180∘−64∘−76∘=40∘，
∵∠1=17∘，
∴∠CNM=180∘−∠12，
在 △CMN 中，∠CMN=180∘−∠C−∠CNM=180∘−40∘−81.5∘=58.5∘，
∴∠2=180∘−2∠CMN=180∘−2×58.5∘=63∘．
（2） 由题意可知：2∠CNM+∠1=180∘，2∠CMN+∠2=180∘，
∴2∠CNM+∠CMN+∠1+∠2=360∘，
∵∠C+∠CNM+∠CMN=180∘，
∴∠CMN+∠CMN=180∘−∠C，
∴2180∘−∠C=360∘−∠1+∠2，
∴∠1+∠2=2∠C．
25. （1） 依题意，得 Δ=−2m+12−4×1×m2=4m+1≥0，
解得 m≥−14．
（2） 答案不唯一，如：m=0，
此时方程为 x2−x=0，
解得 x1=0，x2=1．
26. （1） 如图（1）所示，连接 AP，
∵AB=AC，P 是 BC 中点，
∴AP⊥BC，BP=CP，
在 Rt△ABP 中，AB2=BP2+AP2，
∴AB2−AP2=BP2，
又 ∵BP=CP，
∴BP⋅CP=BP2，
∴AB2−AP2=BP⋅CP．
（2） 成立．
如图（2）所示，连接 AP，作 AD⊥BC，交 BC 于 D，
∵AB=AC，AD⊥BC，
∴BD=CD，
在 Rt△ABD 中，AB2=AD2+BD2．
同理，AP2=AD2+DP2，
∴AB2−AP2=AD2+BD2−AD2+DP2=BD2−DP2，
又 ∵BP=BD+DP，CP=CD−DP=BD−DP，
∴BP⋅CP=BD+DPBD−DP=BD2−DP2，
∴AB2−AP2=BP⋅CP．
（3） AP2−AB2=BP⋅CP．
如图（3），P 是 BC 延长线上任意一点，连接 AP，并作 AD⊥BC，交 BC 于 D，
∵AB=AC，AD⊥BC，
∴BD=CD，
在 Rt△ABD 中，AB2=AD2+BD2，
在 Rt△ADP 中，AP2=AD2+DP2，
∴AP2−AB2=AD2+PD2−AD2+DB2=PD2−BD2，
又 ∵BP=BD+DP，CP=DP−CD=DP−BD，
∴BP⋅CP=BD+DPDP−BD=DP2−BD2，
∴AP2−AB2=BP⋅CP．
27. 设乙商品的进价为 x 元/件，则甲商品的进价为 1+50%x 元/件，
依题意，得：
72001+50%x−3200x=40,
解得：
x=40,
经检验，x=40 是原方程的解，且符合题意，
∴1+50%x=60，3200x=80，72001+50%x=120．
答：甲商品的进价为 60 元/件，乙商品的进价为 40 元/件，购进甲商品 120 件，购进乙商品 80 件．
28. （1） 上述两同学回答的均不全面，应该是：其余两角的大小是 75∘ 和 75∘ 或 30∘ 和 120∘．
理由如下：
①当 ∠A 是顶角时，设底角是 α．
∴30∘+α+α=180∘，α=75∘．
∴ 其余两角是 75∘ 和 75∘．
②当 ∠A 是底角时，设顶角是 β，
∴30∘+30∘+β=180∘，β=120∘．
∴ 其余两角分别是 30∘ 和 120∘．
（2） 感受为：解题时，思考问题要全面，有的题目要进行分类讨论，分类时要做到不重不漏．