专题13.3 垂直平分线（知识讲解）-2021-2022学年八年级数学上册基础知识专项讲练（人教版）

专题13.3  垂直平分线（知识讲解）

【学习目标】

1．理解线段的垂直平分线的概念，掌握线段的垂直平分线的性质及判定，会画已知线段的垂直平分线．

2．能运用线段的垂直平分线的性质解决简单的数学问题及实际问题．

【要点梳理】

定义：

经过线段中点并且垂直于这条线段的直线，叫做这条线段的垂直平分线，也叫线段的中垂线．

性质：

性质1：线段垂直平分线上的点到线段两端点的距离相等；
　  性质2：与一条线段两个端点距离相等的点在这条线段的垂直平分线上．

特别说明：

线段的垂直平分线的性质是证明两线段相等的常用方法之一.同时也给出了引辅助线的方法，那就是遇见线段的垂直平分线，画出到线段两个端点的距离，这样就出现相等线段，直接或间接地为构造全等三角形创造条件.

三角形三边垂直平分线交于一点，该点到三角形三顶点的距离相等，这点是三角形外接圆的圆心——外心.

【典型例题】

类型一、垂直平分线性质 

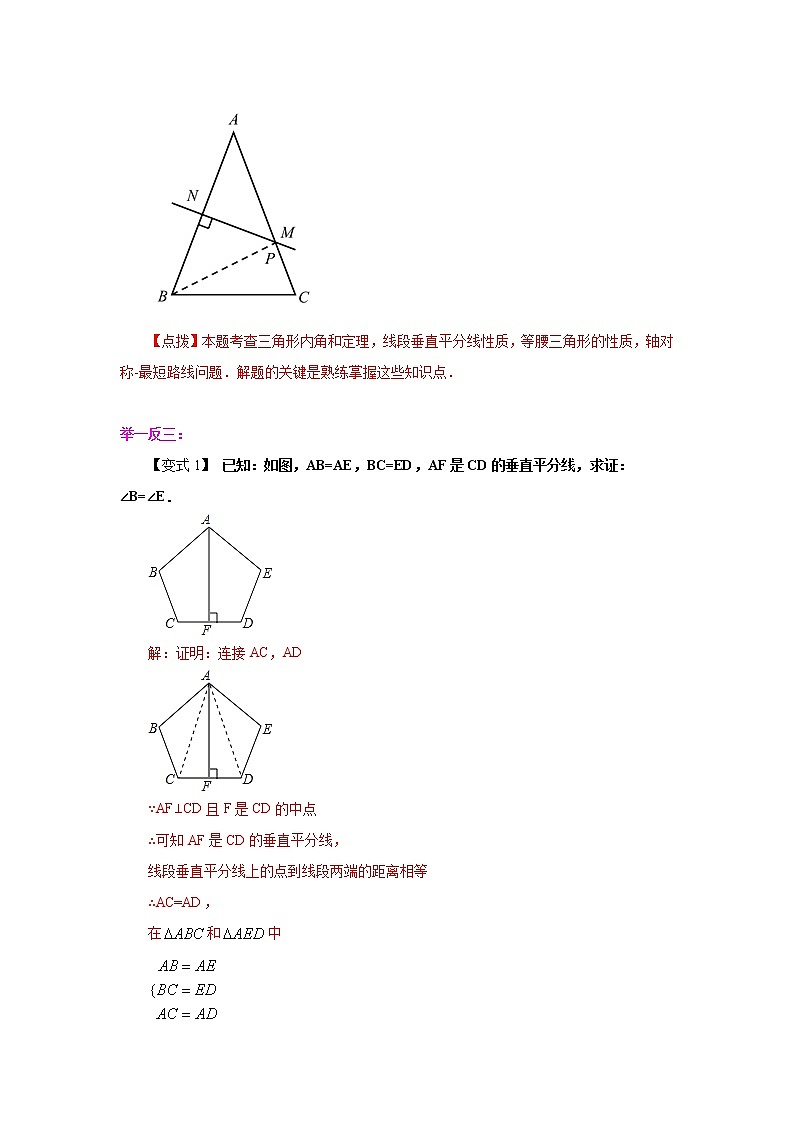
1．如图，在中，，的垂直平分线交于，交于．

（1）若，则的度数是          ；

（2）连接，若，的周长是．

①求的长；

②在直线上是否存在点，使由，，构成的的周长值最小？若存在，标出点的位置并求的周长最小值；若不存在，说明理由．

【答案】（1）50° （2）① 6cm；②存在点P，点P与点M重合，△PBC周长的最小值为

【分析】（1）根据等腰三角形的性质得出∠B＝∠C＝70°,在△ABC中，根据三角形内角和定理求得∠A＝40°，在△AMN中，根据三角形内角和定理求得∠NMA＝50°;

（2）①根据线段垂直平分线可得AM＝BM，根据△MBC的周长＝BM＋BC＋CM＝AM＋BC＋CM即可求解；

②根据对称轴的性质可知，M点就是点P所在的位置，△PBC的周长最小值就是△MBC的周长．

解：（1）∵AB＝AC，

∴∠B＝∠C＝70°，

∴∠A＝180°－70°－70°＝40°

∵MN垂直平分AB交AB于N

∴MN⊥AB, ∠ANM＝90°，

在△AMN中，

∠NMA＝180°－90°－40°＝50°；

（2）①如图所示，连接MB，

∵MN垂直平分AB交于AB于N

∴AM＝BM，

∴△MBC的周长＝BM＋BC＋CM＝AM＋BC＋CM＝BC＋AC＝

又∵AB＝AC＝8cm，

∴BC＝14 cm－8 cm＝6cm；

②如图所示，

∵MN垂直平分AB，

∴点A、B关于直线MN对称，AC与MN交于点M，因此点P与点M重合；

∴△MBC的周长就是△PBC周长的最小值，

∴△PBC周长的最小值＝△MBC的周长＝．

【点拨】本题考查三角形内角和定理，线段垂直平分线性质，等腰三角形的性质，轴对称-最短路线问题．解题的关键是熟练掌握这些知识点．

举一反三：

【变式1】 已知：如图，AB=AE，BC=ED，AF是CD的垂直平分线，求证：∠B=∠E．

解：证明：连接AC，AD

∵AF⊥CD且F是CD的中点

∴可知AF是CD的垂直平分线，

线段垂直平分线上的点到线段两端的距离相等

∴AC=AD，

在和中

【变式2】 已知在△ABC中，∠CAB的平分线AD与BC的垂直平分线DE交于点D，DM⊥AB于M，DN⊥AC的延长线于N．

（1）证明：BM=CN；

（2）当∠BAC=70°时，求∠DCB的度数．

【答案】（1）见解析；（2）∠DCB=35°

【分析】（1）根据角平分线的性质和线段垂直平分线的性质可得到DM=DN，DB=DC，根据HL证明Rt△DMB≌Rt△DNC，即可得出BM=CN；
（2）由HL证明Rt△DMA≌Rt△DNA，得出∠ADM=∠ADN=55°，由于∠BDM=∠CDN，因此∠BDC=110°，因此∠EDC=55°，根据两角互余的关系即可求得∠DCB的度数．

解：（1）证明：连接BD、CD，如图所示：

∵AD是∠CAB的平分线，DM⊥AB，DN⊥AC，

∴DM=DN，

∵DE垂直平分线BC，

∴DB=DC，

在Rt△DMB和Rt△DNC中，

∴Rt△DMB≌Rt△DNC(HL)，

∴BM=CN；

（2）由（1）得：∠BDM=∠CDN，

∵AD是∠CAB的平分线，DM⊥AB，DN⊥AC，

∴DM=DN，

在Rt△DMA和Rt△DNA中，

∴Rt△DMA≌Rt△DNA(HL)，

∴∠ADM=∠ADN

∵∠BAC=70°

∴∠MDN=110°，∠ADM=∠ADN=55°，

∵∠BDM=∠CDN

∴∠BDC=∠MDN=110°

∵AD是BC的垂直平分线

∴∠EDC=55°

∴∠DCB=90°-∠EDC=35°

∴∠DCB=35°

故答案为∠DCB=35°．

【点拨】考查了角平分线的性质、线段垂直平分线的性质以及全等三角形的判定与性质，熟悉角平分线的性质和线段垂直平分线的性质，证明三角形全等是解决问题的关键．

【变式3】 如图，直线l与m分别是边AC和BC的垂直平分线，它们分别交边AB于点D和点E.

（1）若，则的周长是多少？为什么？

（2）若，求的度数.

【答案】（1）10；（2）

【分析】根据垂直平分线定理即可推出，同理，即的周长为10

由垂直平分线定理可得，，再根据三角形内角和定理，即，再由三角形外角和定理得 ，即可计算出.

解：（1）的周长为10

∵l是AC的垂直平分线∴

同理

∴的周长

（2）∵l是AC的垂直平分线∴

同理

∴，

∵①

∴

∵

∴②

联立①②，解得：

【点拨】本题考查垂直平分线和三角形的内角和定理，熟练掌握垂直平分线定理推出=AB是解题关键.

类型二、垂直平分线判定 

2．如图，△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于E，

（1）若∠BAC=50°，求∠EDA的度数；

（2）求证：直线AD是线段CE的垂直平分线．

【答案】（1）65°（2）证明见解析

【分析】（1）由题意可得∠EAD=∠BAC=25°，再根据∠AED=90°，利用直角三角形两锐角互余即可求得答案；

（2）由于DE⊥AB，易得∠AED=90°=∠ACB，而AD平分∠BAC，易知∠DAE=∠DAC，又因为AD=AD，利用AAS可证△AED≌△ACD，那么AE=AC，DE=DC，根据线段垂直平分线的判定定理即可得证.

解：（1）∵AD平分∠BAC，∠BAC=50°，

∴∠EAD=∠BAC=25°，

∵DE⊥AB，

∴∠AED=90°，

∴∠ADE=90°-∠EAD=90°-25°=65°；

（2）∵DE⊥AB，

∴∠AED=90°=∠ACB，

又AD平分∠BAC，

∴∠DAE=∠DAC，

又∵AD=AD，

∴△AED≌△ACD，

∴AE=AC，DE=DC

∴点A在线段CE的垂直平分线上，点D在线段CE的垂直平分线上，

∴直线AD是线段CE的垂直平分线.

【点拨】本题考查了直角三角形两锐角互余、三角形全等的判定与性质、线段垂直平分线的判定等，熟练掌握相关的性质定理与判定定理是解题的关键.

举一反三：

【变式1】 已知，如图，AD是△ABC的角平分线，DE、DF分别是△ABD和△ACD的高。求证：AD垂直平分EF。

【分析】由DE⊥AB,DF⊥AC，得出∠AED=∠AFD；因为AD是△ABC的角平分线，可得∠1=∠2，DE=DF，推出△AED≌△AFD，即AE=AF，所以点A在EF的垂直平分线上，又DE=DF，推出点D在EF的垂直平分线上，即可证明AD垂直平分EF；

解：证明：∵DE⊥AB，DF⊥AC，

∴∠AED=∠AFD，

又∵AD是△ABC的角平分线，

∴∠1=∠2，DE=DF，

∴△AED≌△AFD（AAS），

∴AE=AF，

∴点A在EF的垂直平分线上（到线段两端距离相等的点在线段的垂直平分线上），

∵DE=DF，

∴点D在EF的垂直平分线上，

∴AD垂直平分EF.

【点拨】本题主要考查了等腰三角形的性质，线段垂直平分线的定义，全等三角形的性质，掌握等腰三角形的性质，线段垂直平分线的定义，全等三角形的性质是解题的关键.

【变式2】 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连接AE、BE，BE⊥AE，延长AE交BC的延长线于点F. 已知AD=2cm，BC=5cm.

（1）求证：FC=AD；

（2）求AB的长.   

【答案】（1）证明见解析 ；（2）AB=7cm.

试题分析：（1）根据AD∥BC可知∠ADC=∠ECF，再根据E是CD的中点可求出△ADE≌△FCE，根据全等三角形的性质即可解答．

（2）根据线段垂直平分线的性质判断出AB=BF即可．

试题解析：（1）∵AD∥BC

∴∠ADC=∠ECF ，

∵E是CD的中点，

∴DE=EC ，

∵在△ADE与△FCE中， ，

∴△ADE≌△FCE(ASA) ，

∴FC=AD ；

（2）∵△ADE≌△FCE，

∴AE=EF，AD=CF ，

∵BE⊥AE ，

∴BE是线段AF的垂直平分线，

∴AB=BF=BC+CF，

∵AD=CF ，

∴AB=BC+AD=5+2=7(cm).

【变式3】 如图所示，在中，是平分线，的垂直平分线分别交延长线于点.求证：.

证明：∵平分

∴           (角平分线的定义)

∵垂直平分

∴           （线段垂直平分线上的点到线段两个端点距离相等）

∴（                 ）

∴（等量代换）

∴（                 ）

【答案】，；，；等边对等角；内错角相等，两直线平行.

【分析】根据角平分线的定义，线段垂直平分线的性质，等边对等角解决问题即可.

解：证明:AD平分∠BAC

∴∠BAD＝∠DAC(角平分线的定义)

EF垂直平分AD

∴FD＝FA(线段垂直平分线上的点到线段两个端点距离相等)

∴∠BAD＝∠ADF(等边对等角)

∴∠DAC＝∠ADF(等量代换)

∴DF∥AC(内错角相等两直线平行)

故答案为:BAD，DAC，FD，FA，等边对等角，内错角相等两直线平行

【点拨】本题考查线段的垂直平分线的性质，平行线的判定等知识，解题的关键是熟练掌握基本知识，属于中考常考题型.

类型三、垂直平分线的应用 

3．如图，在△OBC中，边BC的垂直平分线交∠BOC的平分线于点D，连接DB，DC，过点D作DF⊥OC于点F.

(1)若∠BOC＝60°，求∠BDC的度数；

(2)若∠BOC＝，则∠BDC＝        ；（直接写出结果）

(3)直接写出OB，OC，OF之间的数量关系.

【答案】（1）120°；（2）180°－α；（3）OB＋OC＝2OF

【分析】(1)首先过点D作DE⊥OB于E，易证得△DEB≌△DFC（HL），即可得∠BDC=∠EDF，又由∠EOF+∠EDF=180゜，即可求得答案；

(2)由（1），可求得∠BDC的度数;

(3) OB＋OC＝OE＋OF＝2OF

解：(1)过点D作DE⊥OB，交OB延长线于点E，DF⊥OC于F，

∵OD是∠BOC的平分线，
∴DE=DF，
∵DP是BC的垂直平分线，
∴BD=CD，
在Rt△DEB和Rt△DFC中，
∴△DEB≌△DFC（HL）

∴∠BDE=∠CDF，

∴∠BDC=∠EDF，

∵∠EOF+∠EDF=180゜，

∵∠BOC=60゜，

∴∠BDC=∠EDF=120゜．

（2）∵∠EOF+∠EDF=180゜，

∵∠BOC=α，

∴∠BDC=∠EDF=180゜-α．

故答案为：180゜-α．

（3）由（1）知OB＋OC＝OE＋OF＝2OF

【点拨】此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想与转化思想的应用．

举一反三：

【变式1】 如图，中，，，．

（1）用直尺和圆规作的垂直平分线；（保留作图痕迹，不要求写作法）

（2）若（1）中所作的垂直平分线交于点，求的长．

【答案】（1）详见解析；（2）．

【分析】（1）分别以，为圆心，大于为半径画弧，两弧交于点，，作直线即可．

（2）设，在中，利用勾股定理构建方程即可解决问题．

解：（1）如图直线即为所求．

（2）∵垂直平分线段，∴，

设，在中，

∵，∴，

解得，∴．

【点拨】本题考查作图﹣基本作图，线段的垂直平分线的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．

【变式2】 如图，点和点在内部．

（1）请你作出点，使点到点和点的距离相等，且到两边的距离也相等（保留作图痕迹，不写作法）；

（2）请说明作图理由．

【分析】（1）由垂直平分线性质可知点到点和点的距离相等即点P在MN的垂直平分线，由角平分线的性质可知两边的距离相等，即点P在∠AOB的角平分线上.分别作出MN的垂直平分线和∠AOB的角平分线，它们的交点即为所求.

（2）根据作法即可说出理由.

解：（1）如图，作∠AOB的角平分线与线段MN的垂直平分线交于P点，即点到点和点的距离相等，且到两边的距离也相等；

（2）理由：角的平分线上的点到角的两边的距离相等、直平分线上的点到线段两端点的距离相等．

【点拨】本题考查的是复杂作图、角平分线的性质、线段垂直平分线的性质，掌握基本作图的一般步骤、角平分线的性质、线段垂直平分线的性质是解题的关键．

【变式3】 如图，AD为△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，连接EF交AD于点G．

（1）求证：AD垂直平分EF；

（2）若∠BAC=60°，猜测DG与AG间有何数量关系？请说明理由．

【答案】（1）证明见解析；（2）AG=3DG，理由见解析.

【分析】(1)、根据角平分线的性质得出DE=DF，∠AED=∠AFD=90°，从而得出∠DEF=∠DFE，则∠AEF=∠AFE，从而说明AE=AF，即点A、D都在EF的垂直平分线上，得出答案；(2)、根据∠BAC=60°，AD平分∠BAC得出AD=2DE，根据∠EGD=90°，∠DEG=30°得出DE=2DG，从而说明AD=4DG，即AG=3DG.

解：(1)、∵AD为△ABC的角平分线，DE⊥AB，DF⊥AC， ∴DE=DF，∠AED=∠AFD=90°，

∴∠DEF=∠DFE，∴∠AEF=∠AFE，∴AE=AF ∴点A、D都在EF的垂直平分线上，

∴AD垂直平分EF．

(2)、AG=3DG．

∵∠BAC=60°，AD平分∠BAC，∴∠EAD=30°，∴AD=2DE，∠EDA=60°，

∵AD⊥EF，∴∠EGD=90°，∴∠DEG=30°  ∴DE=2DG，∴AD=4DG，  ∴AG=3DG．

考点：(1)、角平分线的性质；(2)、中垂线的性质.

类型四、作图-垂直平分线 

4．如图，在中．

利用尺规作图，在BC边上求作一点P，使得点P到AB的距离的长等于PC的长；

利用尺规作图，作出中的线段PD．

要求：尺规作图，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑

【分析】由点P到AB的距离的长等于PC的长知点P在平分线上，再根据角平分线的尺规作图即可得（以点A为圆心，以任意长为半径画弧，与AC、AB分别交于一点，然后分别以这两点为圆心，以大于这两点距离的一半长为半径画弧，两弧交于一点，过点A及这个交点作射线交BC于点P，P即为要求的点）；

根据过直线外一点作已知直线的垂线的尺规作图即可得（以点P为圆心，以大于点P到AB的距离为半径画弧，与AB交于两点，分别以这两点为圆心，以大于这两点间距离一半长为半径画弧，两弧在AB的一侧交于一点，过这点以及点P作直线与AB交于点D，PD即为所求）．

解：如图，点P即为所求；

如图，线段PD即为所求．

【点拨】本题考查了作图-复杂作图、角平分线的性质定理等知识，解题的关键是熟练掌握基本作图，灵活运用所学知识解决问题．

举一反三：

【变式1】 尺规作图：校园有两条路OA、OB，在交叉路口附近有两块宣传牌C、D，学校准备在这里安装一盏路灯，要求灯柱的位置P离两块宣传牌一样远，并且到两条路的距离也一样远，请你帮助画出灯柱的位置P．（不写画图过程，保留作图痕迹）

【分析】分别作线段CD的垂直平分线和∠AOB的角平分线，它们的交点即为点P．

解答：如图，点P为所作．

【点拨】本题考查了作图−应用与设计作图，熟知角平分线的性质与线段垂直平分线的性质是解答此题的关键．

【变式2】 如图，在△ABC中，点P是AC上一点，连接BP，求作一点M，使得点M到AB和AC两边的距离相等，并且到点B和点P的距离相等．（不写作法，保留作图痕迹）

【分析】根据角平分线的作法、线段垂直平分线的作法作图即可．

解答：如图，点M即为所求，

作法：如解图，以点为圆心，适当长为半径画弧，分别交、于、两点，再分别以、为圆心，以大于长为半径画弧，两弧交于点，连接；以、为圆心，以大于长为半径画弧，两弧分别交于、，连接，则的延长线与的延长线的交点即为所求的点.

【点拨】本题考查的是复杂作图、角平分线的性质、线段垂直平分线的性质，掌握基本尺规作图的一般步骤是解题的关键．

【变式3】 已知，按下列要求：（尺规作图，保留痕迹，不写作法）

（1）作边上的高；

（2）作的平分线．（尺规作图）

（3）作出线段的垂直平分线．（尺规作图）

【分析】（1）根据钝角三角形高的做法即可；

（2）根据角平分线的尺规作图方法即可；

（3）根据线段垂直平分线的尺规作图方法即可．

解：（1）如图所示：AD为BC边上的高．

（2）如图所示：BE为△ABC的平分线．

（3）如图所示：为线段的垂直平分线．

【点拨】本题考查了钝角三角形的高、角平分线、线段垂直平分线的尺规作图，解题的关键掌握相应的作图方法