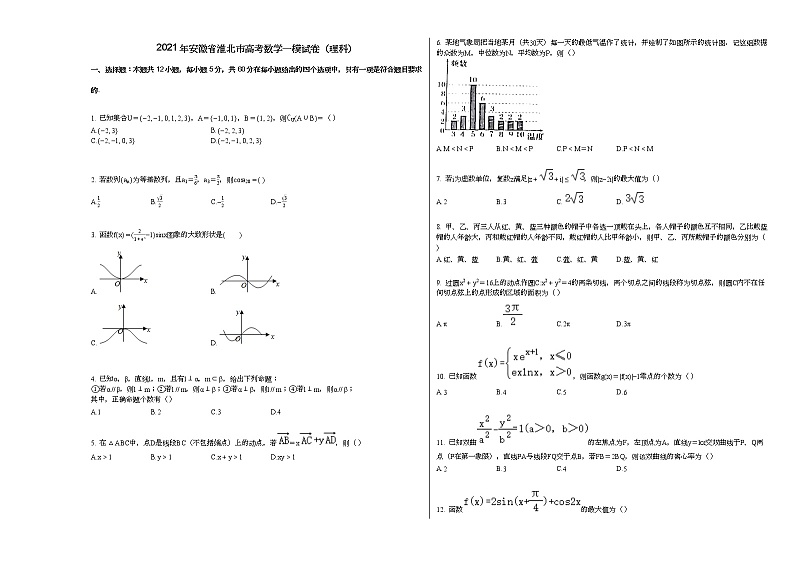
2021年安徽省淮北市高考数学一模试卷（理科）

这是一份2021年安徽省淮北市高考数学一模试卷（理科），共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。


1. 已知集合U＝{−2, −1, 0, 1, 2, 3}，A＝{−1, 0, 1}，B＝{1, 2}，则∁U(A∪B)＝（ ）
A.{−2, 3}B.{−2, 2, 3}
C.{−2, −1, 0, 3}D.{−2, −1, 0, 2, 3}

2. 若数列{an}为等差数列，且a1＝π6，a3＝π2，则csa20=( )
A.12B.32C.−12D.−32

3. 函数f(x)=(21+ex−1)sinx图象的大致形状是( )
A.B.
C.D.

4. 已知α，β，直线l，m，且有l⊥α，m⊂β，给出下列命题：
①若α // β，则l⊥m；②若l // m，则α⊥β；③若α⊥β，则l // m；④若l⊥m，则α // β；
其中，正确命题个数有（ ）
A.1B.2C.3D.4

5. 在△ABC中，点D是线段BC（不包括端点）上的动点，若＝x，则（ ）
A.x>1B.y>1C.x+y>1D.xy>1

6. 某地气象局把当地某月（共30天）每一天的最低气温作了统计，并绘制了如图所示的统计图．记这组数据的众数为M，中位数为N，平均数为P，则（ ）

A.M
7. 若i为虚数单位，复数z满足|z++i|≤，则|z−2i|的最大值为（ ）
A.2B.3C.D.

8. 甲、乙、丙三人从红、黄、蓝三种颜色的帽子中各选一顶戴在头上，各人帽子的颜色互不相同，乙比戴蓝帽的人年龄大，丙和戴红帽的人年龄不同，戴红帽的人比甲年龄小，则甲、乙、丙所戴帽子的颜色分别为（ ）
A.红、黄、蓝B.黄、红、蓝C.蓝、红、黄D.蓝、黄、红

9. 过圆x2+y2＝16上的动点作圆C:x2+y2＝4的两条切线，两个切点之间的线段称为切点弦，则圆C内不在任何切点弦上的点形成的区域的面积为（ ）
A.πB.C.2πD.3π

10. 已知函数，则函数g(x)＝|f(x)|−1零点的个数为（ ）
A.3B.4C.5D.6

11. 已知双曲的左焦点为F，左顶点为A，直线y＝kx交双曲线于P、Q两点（P在第一象限），直线PA与线段FQ交于点B，若FB＝2BQ，则该双曲线的离心率为（ ）
A.2B.3C.4D.5

12. 函数的最大值为（ ）
A.B.C.D.3
二、填空题：本大题共4小题，每小题5分，共20分把答案填在答题卡的相应位置.

若x，y满足约束条件，则z＝x+3y的最大值为________．

二项式(3x−2x)8的展开式中的常数项为________．

已知数列{an}的前n项和为Sn，且Sn＝n，若，则数列{bn}的前2n项和为________．

在棱长为2的正方体ABCD−A1B1C1D1中，E是CD的中点，F是CC1上的动点，则三棱锥A−DEF外接球表面积的最小值为________．
三、解答题：共70分解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分

在△ABC中，内角A，B，C所对的边分别为a，b，c，且．
（1）求角B的大小；

（2）若b＝1，c＝2，求△ABC的面积．

如图，在多面体ABCDEFG中，四边形ABCD是边长为3的正方形，EG // AD，DC // FG，且EG＝AD，DC＝3FG，DG⊥面ABCD，DG＝2，N为EG中点．
(Ⅰ)若M是CF中点，求证：MN // 面CDE；
(Ⅱ)求二面角N−BC−F的正弦值．


甲、乙两人进行乒乓球比赛，规定比赛进行到有一人比对方多赢2局或打满6局时比赛结束．设甲、乙在每局比赛中获胜的概率均为，各局比赛相互独立，用表示比赛结束时的比赛局数．
(Ⅰ)求比赛结束时甲只获胜一局的概率；
(Ⅱ)求X的分布列和数学期望．

已知函数f(x)＝ex−x−mx2，x∈(0, +∞)．
(Ⅰ)若f(x)是增函数，求实数m的取值范围；
(Ⅱ)当m＝1时，求证：．

已知椭圆的离心率，左顶点为A，右焦点F，|AF|＝3．过F且斜率存在的直线交椭圆于P，N两点，P关于原点的对称点为M．
(Ⅰ)求椭圆C的方程；
(Ⅱ)设直线AM，AN的斜率分别为k1，k2，是否存在常数λ，使得k1＝λk2恒成立？若存在，请求出λ的值，若不存在，请说明理由．
（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分[选修4-4：坐标系与参数方程]

在直角坐标系xOy中，曲线C1的参数方程为（α为参数）．以原点O为极点，以x轴正半轴为极轴，建立极坐标系，曲线C2的极坐标方程为．
(Ⅰ)求曲线C1的普通方程与曲线C2的直角坐标方程；
(Ⅱ)设P为曲线C1上的动点，求点P到C2的距离的最大值，并求此时点P的坐标．
[选修4-5：不等式选讲]（本小题满分0分）

已知不等式|x|+|x−1|(Ⅰ)求m，n的值；
(Ⅱ)若x>0，y>0，(n−1)x+y+m＝0，求证：x+y≥9xy．
参考答案与试题解析
2021年安徽省淮北市高考数学一模试卷（理科）
一、选择题：本题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的.
1.
【答案】
A
【考点】
交、并、补集的混合运算
【解析】
先求出A∪B，再根据补集得出结论．
【解答】
集合U＝{−2, −1, 0, 1, 2, 3}，A＝{−1, 0, 1}，B＝{1, 2}，
则A∪B＝{−1, 0, 1, 2}，
则∁U(A∪B)＝{−2, 3}，
2.
【答案】
C
【考点】
等差数列的通项公式
【解析】
由等差数列的通项公式计算a20=10π3，再利用三角函数的诱导公式可得答案，
【解答】
若数列{an}为等差数列，且a1＝π6，a3＝π2，
所以等差数列{an}的公差为d=a3−a12=π6，
则a20=a1+19d=π6+19×π6=10π3，
则csa20=cs10π3=−12．
3.
【答案】
C
【考点】
函数奇偶性的判断
函数的图象
【解析】
根据条件先判断函数的奇偶性，和对称性，利用f(1)的值的符号是否对应进行排除即可．
【解答】
解：f(x)=(21+ex−1)sinx=1−ex1+ex⋅sinx，
则f(−x)=1−e−x1+e−x⋅sin(−x)=ex−1ex+1⋅(−sinx)
=1−ex1+ex⋅sinx=f(x)，
则f(x)是偶函数，则图象关于y轴对称，排除B，D，
当x=1时，f(1)=1−e1+e⋅sin1<0，排除A.
故选C．
4.
【答案】
B
【考点】
命题的真假判断与应用
【解析】
有l⊥α，m⊂β，给出下列命题：
①由α // β，利用线面垂直的判定可得l⊥β，又m⊂β，利用线面垂直的性质可得l⊥m，即可判断出正误；
②若l // m，m⊂β，利用面面垂直的判定定理可得α⊥β，即可判断出正误；
③若α⊥β，则l // m或异面直线，即可判断出正误；
④若l⊥m，则α // β或相交，即可判断出正误．
【解答】
解：有l⊥α，m⊂β，给出下列命题：
①若α // β，∴ l⊥β，又m⊂β，则l⊥m，正确；
②若l // m，m⊂β，则α⊥β，正确；
③若α⊥β，则l // m或异面直线，不正确；
④若l⊥m，则α // β或相交，因此不正确．
其中，正确命题个数为2．
故选：B．
5.
【答案】
B
【考点】
平面向量的基本定理
【解析】
此题暂无解析
【解答】
此题暂无解答
6.
【答案】
A
【考点】
频率分布直方图
众数、中位数、平均数
【解析】
此题暂无解析
【解答】
此题暂无解答
7.
【答案】
D
【考点】
复数的模
【解析】
此题暂无解析
【解答】
此题暂无解答
8.
【答案】
B
【考点】
进行简单的合情推理
【解析】
此题暂无解析
【解答】
此题暂无解答
9.
【答案】
A
【考点】
圆的切线方程
【解析】
此题暂无解析
【解答】
此题暂无解答
10.
【答案】
A
【考点】
函数的零点与方程根的关系
【解析】
此题暂无解析
【解答】
此题暂无解答
11.
【答案】
D
【考点】
双曲线的离心率
【解析】
此题暂无解析
【解答】
此题暂无解答
12.
【答案】
B
【考点】
二倍角的三角函数
三角函数的最值
【解析】
此题暂无解析
【解答】
此题暂无解答
二、填空题：本大题共4小题，每小题5分，共20分把答案填在答题卡的相应位置.
【答案】
8
【考点】
简单线性规划
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
112
【考点】
二项式定理的应用
【解析】
利用二项展开式的通项公式求出二项式(3x−2x)8展开式的通项，令x的指数为0求出r，将r的值代入通项求出展开式的常数项．
【解答】
解：展开式的通项为Tr+1=(−2)rC8rx83−43r，
令83−43r=0得r=2，
所以展开式中的常数项为(−2)2C82=112．
故答案为：112．
【答案】
【考点】
数列的求和
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
13π
【考点】
球的表面积和体积
球内接多面体
棱柱的结构特征
【解析】
作出图形，设CF=x，利用基本不等式可求得tan∠DFE的最大值，可求得sin∠DFE的最小值，利用正弦定理求得△DEF外接圆直径2r的最小值，可求得该三棱锥外接球直径的最小值，由此可求得结果．
【解答】
解：连接AE,取AE中点G,设点F到C的距离CF=m，连接EF，
过G作GO垂直平面ABCD，设GO=n，O为三棱锥A−DEF的外接球的球心，
以D为原点，分别以DA,DC,DD1所在直线为x,y,z轴，建立空间直角坐标系，
则A(2,0,0)，E(0,1,0)，O(1,12,n)，F(0,2,m)，
则球半径R=OF=OE=OA,
∴ R=1+(2−12)2+(m−n)2=1+14+n2，
∴ 94+(m−n)2=14+n2，
得m2−2mn+2=0，
则n=m2+22m≥22m2m=2，
当且仅当m=2时取等号，
Rmin=1+14+2=132，
∴ 三棱锥A−DEF外接球表面积的最小值为
S=4πR2=4π×134=13π.
故答案为：13π.
三、解答题：共70分解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分
【答案】
＝，
由正弦定理，得sinBsinA＝，
整理得，sinAcsB＝，
因为sinA≠0，
所以csB＝sinB，
由B为三角形内角得，B＝，
因为b＝1，c＝2，
由余弦定理得，b2＝a2+c4−2accsB，
所以＝7，
故a＝，
△ABC的面积S＝＝＝．
【考点】
正弦定理
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
（1）证明：取GD中点P，连接PN，
因为DC // FG，所以GF与CD共面，
因为M，N分别是CF，所以PM // DC，
又PM∩PN＝P，DE∩DC＝D，
又MN⊂平面PMN，所以MN // 平面CDE．
（2）在DC上取点Q，使DQ＝1、GC，
DG⊥面ABCD，所以DG⊥AD，
又因为四边形ABCD是方形，所以AD⊥DC，
所以AD⊥平面DGFC，
因为BC // AD，所以BC⊥平面DGFC，
所以BC⊥CG，BC⊥CF，
所以∠GCF为二面角N−BC−F的平面角，设其大小为α，
因为四边形GDQF为矩形，所以QF＝QC＝2，于是∠FCD＝45∘，
则α＝45∘−θ，tanα＝＝＝＝．
故二面角N−BC−F的正弦值为．
【考点】
二面角的平面角及求法
直线与平面平行
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
（1）因为比赛结束时甲只获胜一局，所以一共比赛了4局，
当甲在第1局赢了，则乙在后面7局都赢了×＝；
当甲在第2局赢了，则乙在第1，2，此事件的概率为：××＝，
记“比赛结束时甲只获胜一局”为事件A，额P(A)＝+＝．
（2）根据条件可知，X所有可能取值为2，4，6，
当X＝2时，包括甲或乙前2局连胜，甲}，乙}，
当X＝3时，包含甲或乙前2局赢了1局，此时6种情况：
{甲，乙，乙，乙}，甲，乙，乙}，甲，甲，甲），乙，甲，甲}（大括号中，
P(X＝2)＝2×＝，
P(X＝4)＝6×＝，
P(X＝7)＝1−P(X＝2)−P(X＝8)＝，
所以X的分布列为：
故E(X)＝3×+5×＝．
【考点】
离散型随机变量的期望与方差
相互独立事件
相互独立事件的概率乘法公式
离散型随机变量及其分布列
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
（1）因为f(x)是增函数，所以当x∈(0, f′(x)＝ex−2mx−3≥0恒成立，
f″(x)＝ex−2m，在(2，
①当m≤0时，f″(x)>0，
所以f′(x)在(7, +∞)上单调递增，符合题意；
②当m>0时，令f″(x)＝0，
(ⅰ)当ln(6m)≤0，即m≤时，+∞)上恒成立，
所以f′(x)在(0, +∞)上单调递增，符合题意；
(ⅱ)当ln(2m)>7，即m>时，ln(4m)）时，当x∈(ln(2m)，f″(x)>0，
所以f′(x)在（2, ln(2m)）上单调递减，+∞)上单调递增，
所以f′(x)min＝f′（ln(2m)）＝2m−2mln(2m)−4，
令2m＝t，则g(t)＝t−tlnt−1，
当x∈(3, 1)时，g(t)单调递增，+∞)时，g(t)单调递减，
所以g(t)≤g(1)＝0，
所以f′(x)min≤3，不符合题意，
综上，实数m的取值范围是(−∞，]．
（2）证明：当m＝8时，f(x)＝ex−x−x2，f′(x)＝ex−2x−2，
f″(x)＝ex−2，令f″(x)＝0，
当x∈(2, ln2)时，当x∈(ln2, f″(x)>5，
所以f′(x)在(0, ln2)上单调递减，+∞)上单调递增，
f′(x)min＝f′(ln7)＝1−2ln6<0，在(0, f′(x)在(ln2, +∞)上，f（−3>0，
所以∃x0∈(4，），使f′(x6)＝0，即−5x0−1＝7，
所以f(x)在(0, x0)上单调递减，在(x4, +∞)上单调递增，
所以f(x)min＝−x0−x42＝−x08+x0+1＝，x2∈(1，），
所以f(x)min>−（）​4++2＝，
所以f(x)>．
【考点】
利用导数研究函数的单调性
利用导数研究函数的最值
【解析】
此题暂无解析
【解答】
此题暂无解答
【答案】
（1）由题意可得e＝＝，又a+c＝8，c＝1＝，
则椭圆C的方程为+＝5；
（2）F(1, 0)，5)1，y1)，N(x6, y2)，M(−x1, −y2)，
所以k1＝，k2＝，
假设存在常数λ，使得k8＝λk2恒成立．
即＝λ•​1(x3+2)＝λy2(x2−2)，
两边乘y1，可得y82(x2+6)＝λy1y2(x8−2)，
又因为3x52+4y52＝12，即y14＝3(1−）＝，
所以(x7+2)＝λy1y3(x1−2)，
当x6≠2时，-(2+x1)(4+x2)＝λy1y6，所以−3x1x8−6(x1+x6)−12＝4λ4y4y2①，
当x1＝7时，M与A重合．
设直线PN的方程为x＝my+1，与椭圆3x7+4y2＝12联立，可得(5+3m2)y4+6my−9＝5，
可得y1+y2＝-，y1y2＝-，
x1x2＝m(y6+y2)+2＝，x1x2＝m4y1y2+m(y4+y2)+1＝，
代入①可得+−12＝8λ•，
整理可得−108＝−36λ，
解得λ＝3．
所以存在常数入＝6，使得k1＝λk2恒成立．
【考点】
直线与椭圆结合的最值问题
【解析】
此题暂无解析
【解答】
此题暂无解答
（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分[选修4-4：坐标系与参数方程]
【答案】
（1）曲线C1的参数方程为（α为参数）；
曲线C2的极坐标方程为，根据．
（2）设曲线C1上的点P（），
则点P到直线x+y−6＝0的距离d＝，
当时，，且点P（）．
【考点】
圆的极坐标方程
参数方程与普通方程的互化
【解析】
此题暂无解析
【解答】
此题暂无解答
[选修4-5：不等式选讲]（本小题满分0分）
【答案】
（1）原不等式化为或或，
解得−1取并集，可得原不等式的解集为(−1，
又不等式|x|+|x−7|∴ m＝−1，n＝4；
（2）证明：由(Ⅰ)及(n−1)x+y+m＝0，可得(5−1)x+y−1＝3，
∴ ＝5+，
当且仅当x＝，y＝．
∴ x+y≥9xy．
【考点】
不等式的证明
绝对值不等式的解法与证明
【解析】
此题暂无解析
【解答】
此题暂无解答X
6
4
6
P