




人教版新课标A选修2-22.2直接证明与间接证明图文ppt课件
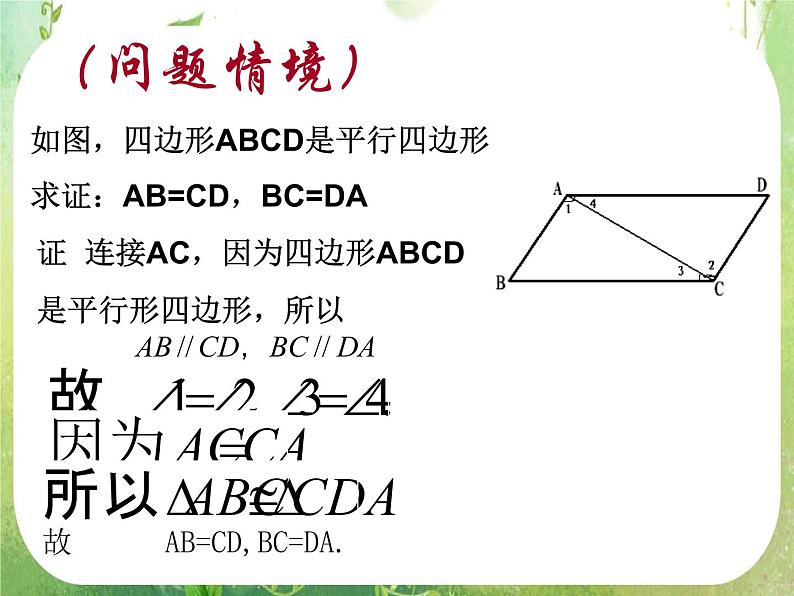
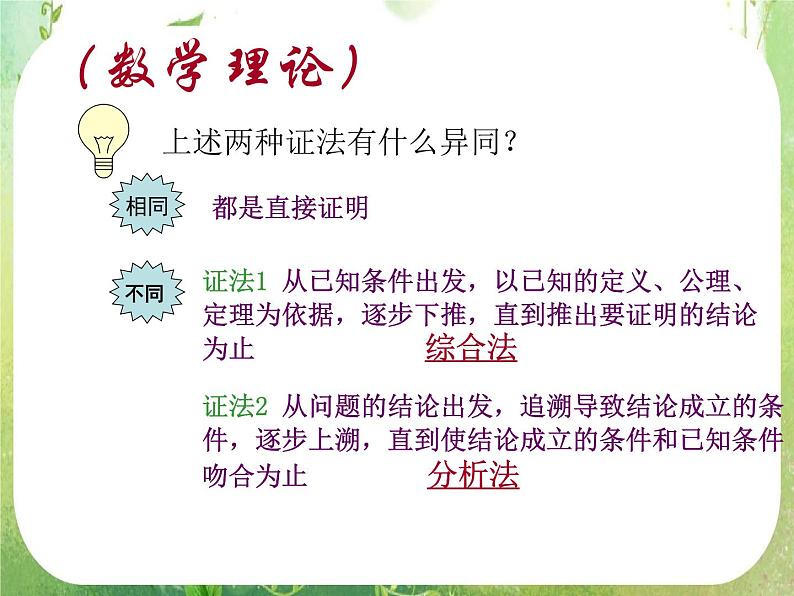
展开教学目标: 结合已经学过的数学实例,了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点.教学重点:会用综合法证明问题;了解综合法的思考过程.教学难点: 根据问题的特点,结合综合法的思考过程、特点,选择适当的证明方法.(问题情境)如图,四边形ABCD是平行四边形求证:AB=CD,BC=DA证 连接AC,因为四边形ABCD是平行形四边形,所以故 AB=CD,BC=DA.1 概念 直接从原命题的条件逐步推得命题成立2 直接证明的一般形式:(学生活动)证法1 对于正数a,b, 有证法2 要证只要证只要证只要证因为最后一个不等式成立,故结论成立。(数学理论)上述两种证法有什么异同?都是直接证明证法1 从已知条件出发,以已知的定义、公理、定理为依据,逐步下推,直到推出要证明的结论为止 综合法相同不同 证法2 从问题的结论出发,追溯导致结论成立的条件,逐步上溯,直到使结论成立的条件和已知条件吻合为止 分析法综合法和分析法的推证过程如下:综合法已知条件结论分析法结论 已知条件 (例题)证 (综合法) 因为因为所以又因为所以所以所以证 (分析法)要证明CE=DF,只需证明为此只需证明为了证明 只需 为了证明 只需证明 也只需 因为 是对顶角,所以它们相等,从而 成立,因此命题成立. 分析法 解题方向比较明确, 利于寻找解题思路; 综合法 条理清晰,易于表述。通常以分析法寻求思路,再用综合法有条理地表述解题过程(练习)(练习)证要证只需证明只需证明只需证明所以原命题成立.3.△ABC三边长的倒数成等差数列,求证:. 证明:因为a,b,c为△ABC三边 所以 a + c > b 所以 cosB>0 因此(回顾小结)分析法 解题方向比较明确, 利于寻找解题思路; 综合法 条理清晰,易于表述。通常以分析法寻求思路,再用综合法有条理地表述解题过程分析法综合法概念 用分析法去思考,寻找证题途径,用综合法进行书写;或者联合使用分析法与综合法,即从“欲知”想“需知”(分析),从“已知”推“可知”(综合),双管齐下,两面夹击,逐步缩小条件与结论之间的距离,找到沟通已知条件和结论的途径.
2020-2021学年2.1合情推理与演绎推理教学演示课件ppt: 这是一份2020-2021学年2.1合情推理与演绎推理教学演示课件ppt
数学选修2-22.1合情推理与演绎推理教学课件ppt: 这是一份数学选修2-22.1合情推理与演绎推理教学课件ppt
高中数学人教版新课标A选修2-22.2直接证明与间接证明教案配套课件ppt: 这是一份高中数学人教版新课标A选修2-22.2直接证明与间接证明教案配套课件ppt













