数学人教版新课标A第三章 空间向量与立体几何综合与测试导学案

高二二部数学学案NO.29

立体几何中的向量方法——利用空间向量求空间角

设计人：李凤英  审核人：苏瑞娟  时间：12.31

【课程标准】

能用向量法解决线线、线面、面面的夹角的计算问题，体会向量方法在研究几何问题中的作用

【学习目标】

1、使学生学会求异面直线所成的角、直线与平面所成的角、二面角的向量方法；

2、使学生能够应用向量方法解决一些简单的立体几何问题；

3、使学生的分析与推理能力和空间想象能力得到提高.

【自主学习】

1. 异面直线所成的角、线面角、二面角的范围分别是什么？

2.两向量的夹角的范围是什么？

3、向量的有关知识

（1）两向量数量积的定义：

（2）两向量夹角公式：

（3）什么是直线的方向向量？什么是平面的法向量？

【典型例题】

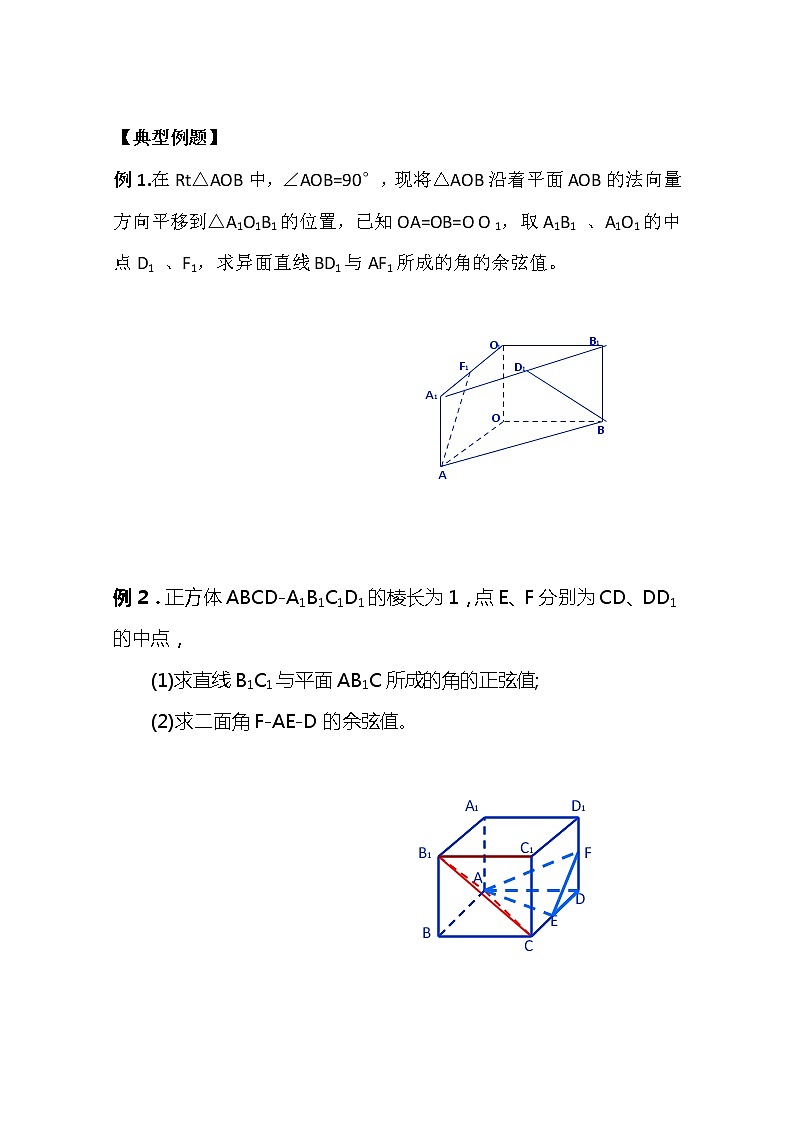
例1.在Rt△AOB中，∠AOB=90°，现将△AOB沿着平面AOB的法向量方向平移到△A1O1B1的位置，已知OA=OB=O O 1，取A1B1 、A1O1的中点D1 、F1，求异面直线BD1与AF1所成的角的余弦值。

                                                                                                                                                              例2．正方体ABCD-A1B1C1D1的棱长为1，点E、F分别为CD、DD1的中点，

(1)求直线B1C1与平面AB1C所成的角的正弦值;

(2)求二面角F-AE-D的余弦值。                                                                                                                                      

例3            如图，甲站在水库底面上的点A处，乙站在水坝斜面上的点B处.从A，B到直线 （库底与水坝的交线）的距离AC和BD分别为 a 和b,CD的长为c , AB的长为d .求库底与水坝所成二面角的余弦值.

巩固练习：如图，已知：直角梯形OABC中，OA∥BC，∠AOC=90°，SO⊥平面OABC，且OS=OC=BC=1，OA=2.求

⑴异面直线SA和OB所成的角的余弦值；

 ⑵OS与平面SAB所成角α的正弦值；                                

 ⑶二面角B－AS－O的余弦值.                                        

教学过程

一、复习引入

1、用空间向量解决立体几何问题的“三步曲”

（1）建立立体图形与空间向量的联系，用空间向量表示问题中涉及的点、直线、平面，把立体几何问题转化为向量问题；

（化为向量问题）

（2）通过向量运算，研究点、直线、平面之间的位置关系以及它们之间距离和夹角等问题；

（进行向量运算）

（3）把向量的运算结果“翻译”成相应的几何意义。（回到图形）

二、知识讲解与典例分析

知识点1、异面直线所成的角（范围：              ）

（1）定义：过空间任意一点o分别作异面直线a与b的平行线a´与b´，那么直线a´与b´ 所成的不大于90°的角     ，叫做异面直线a与b 所成的角。

（2）用向量法求异面直线所成角

设两异面直线a、b的方向向量分别为     和  ，

问题1   当与的夹角不大于90°时，异面直线a、b 所成的角     与 和 的夹角的关系？      相等

问题 2   当与的夹角大于90°时，异面直线a、b 所成的角    与和  的夹角的关系？       互补

所以，异面直线a、b所成的角的余弦值为

典型例题1：在Rt△AOB中，∠AOB=90°，现将△AOB沿着平面AOB的法向量方向平移到△A1O1B1的位置，已知OA=OB=Oo1，取A1B1 、A1O1的中点D1 、F1，求异面直线BD1与AF1所成的角的余弦值。

      解：以点O为坐标原点建立空间直角坐标系，并设OA=1,则A(1,0,0)     B(0,1,0)    F1( ,0,1)    D1( , ,1)

所以，异面直线BD1与AF1所成的角的余弦值为

知识点2、直线与平面所成的角（范围：              ）

据图分析出直线与平面所成的角的正弦值为      =     

典型例题2:正方体ABCD-A1B1C1D1的棱长为1，点E、F分别为CD、DD1的中点，

    (1)求直线B1C1与平面AB1C所成的角的正弦值;

    (2)求二面角F-AE-D的余弦值。

解： (1)以点A为坐标原点建立空间直角坐标系,如图所示，则：

A(0,0,0)         B1(1,0,1)            C(1,1,0)          C1(1,1,1)

3、二面角（范围：              ）

典型例题2  (2)点E、F分别为CD、DD1的中点，求二面角F-AE-D的余弦值。

典型例题3  如图，甲站在水库底面上的点A处，乙站在水坝斜面上的点B处.从A，B到直线 （库底与水坝的交线）的距离AC和BD分别为 a 和 b ,CD的长为c , AB的长为d .求库底与水坝所成二面角的余弦值.

解：如图

根据向量的加法法则,

于是，得

设向量 与 的夹角为，就是库与水坝所成的二面角.

因此  

所以  

库底与水坝所成二面角的余弦值是

三、巩固练习

如图，已知：直角梯形OABC中，OA∥BC，∠AOC=90°，SO⊥平面OABC，且OS=OC=BC=1，OA=2.求 

⑴异面直线SA和OB所成的角的余弦值；

⑵直线OS与平面SAB所成角α的正弦值；

⑶二面角B－AS－O的余弦值.

四、课堂小结

   1、异面直线所成的角 

2、直线和平面所成的角

   3、二面角                         或

五、布置作业           课本第112页A组第6题