2021学年一 圆周角定理教课内容ppt课件

这是一份2021学年一 圆周角定理教课内容ppt课件，共30页。PPT课件主要包含了解析如图所示等内容，欢迎下载使用。

1．理解圆周角定理．2．理解圆心角定理及其推论．3．能正确应用以上定理解决几何问题．
1．圆周角定理：圆上一条弧所对的圆周角等于它所对的圆心角的________．应当注意的是，圆周角与圆心角一定是对着__________，它们才有上面定理中所说的数量关系．2．圆心角定理：圆心角的度数________它所对弧的度数．3．圆周角定理的推论：推论1：同弧或等弧所对的圆周角________；同圆或等圆中，相等的圆周角所对的弧________．推论2：半圆(或直径)所对的圆周角是________；90°的圆周角所对的弦是________．
1．一半　同一条弧　2.等于　3.相等　也相等 直角　直径
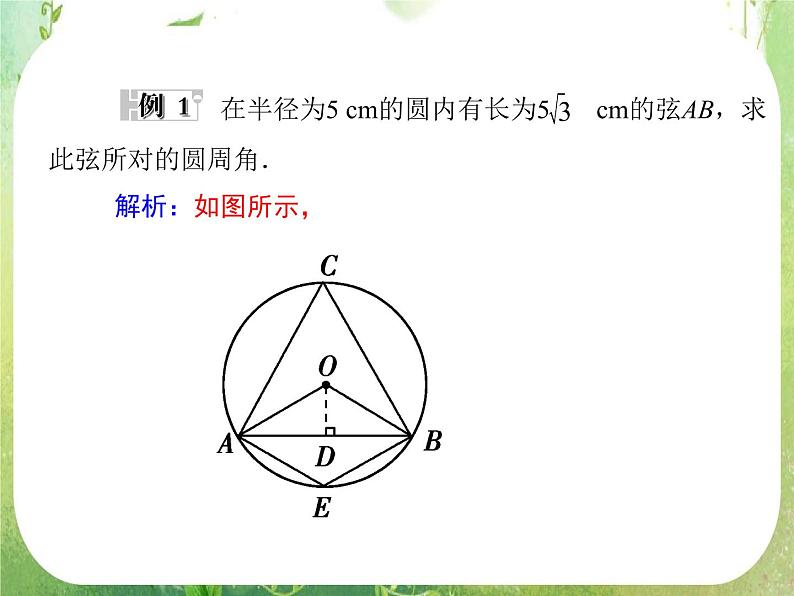
在半径为5 cm的圆内有长为5 cm的弦AB，求此弦所对的圆周角．
点评：弦所对的圆周角有两个，易丢掉120°而导致错误．另外，求圆周角时应用到解三角形的知识．
如图所示，已知在⊙O中，∠AOB＝2∠BOC，求证：∠ACB＝2∠BAC.　　　　　　　　证明：∵∠ACB＝ ∠AOB，∠AOB＝2∠BOC，∴∠ACB＝∠BOC.∵∠BAC＝ ∠BOC，∴∠ACB＝2∠BAC.点评：只要是在圆中考查角的关系，那么就要考虑弧的中介作用．
已知AD是△ABC的高，AE是△ABC的外接圆的直径，求证：∠BAE＝∠DAC.分析：题目中出现圆的直径，想到直径所对的圆周角是直角．因此，连结BE，得到∠ABE＝90°，同时，在△ABE与△ADC中，又有同弧所对的圆周角∠C与∠E相等，从而结论得以证明．
证明：如图，连接BE，∵AE为直径，∴∠ABE＝90°.∵AD是△ABC的高，所以∠ADC＝90°，∴∠ADC＝∠ABE.∵∠E＝∠C，∴∠BAE＝180°－∠ABE－∠E，∠DAC＝180°－∠ADC－∠C，∴∠BAE＝∠DAC.
1.下列命题中，真命题的个数是（）①顶点在圆周上的角是圆周角；②圆周角的度数等于圆心角度数的一半；③90°的圆周角所对的弦是直径;④直径所对的角是直角；⑤圆周角相等，则它们所对的弦也相等；⑥同弧或等弧所对的圆周角相等.A .1个 B. 2个 C. 3个 D. 4个
2.已知点O是△ABC的外心，∠A=α，则∠BOC为（ ）A. 2α B. 360°-2αC. 2α或360°-2α D. 180°-2α
3．如图所示，若圆内接四边形的对角线交于点E，则图中相似三角形有(　　)A．1对 B．2对C．3对 D．4对
4．如图所示，D是 的中点，与∠ABD相等的角的个数是(　　)A．7个 B．3个C．2个 D．1个
解析：由同弧或等弧所对的圆周角相等可知∠ABD＝∠CBD＝∠ACD＝∠DAC，故与∠ABD相等的角有3个．答案：B
5．已知D、C是以AB为直径的圆弧上的两点，若 所对的圆周角为25°， 所对的圆周角为35°，则 所对的圆周角为(　　)A．30° B．40°C．30°或80° D．80°
6．如图所示，已知AB是半圆O的直径，弦AD、BC相交于点P，那么 等于(　　)A．sin∠BPD B．cs∠BPDC．tan∠BPD D.
7．在Rt△ABC中，∠C＝90°，∠A＝30°，b＝2 ，则此三角形外接圆半径为(　　)A. B．2C．2 D．48．如图所示，⊙O直径MN⊥AB于点P，∠BMN＝30°，则∠AON＝________.
9．如图所示，已知AB是⊙O的直径，CD与AB相交于点E，∠ACD＝60°，∠ADC＝45°，则∠AEC＝________.
10．如图所示，已知⊙O为△ABC的外接圆，AB＝AC＝6，弦AE交BC于点D.若AD＝4，则AE＝________.
11．如图，AB是圆O的直径，D，E为圆O上位于AB异侧的两点，连接BD并延长至点C，使BD＝DC，连接AC，AE，DE.求证：∠E＝∠C.
证明：如图，连接OD，因为BD＝DC，O为AB的中点，所以OD∥AC，于是∠ODB＝∠C.因为OB＝OD，所以∠ODB＝∠B.于是∠B＝∠C.因为点A，E，B，D都在圆O上，且D，E为圆O上位于AB异侧的两点，所以∠E和∠B为同弧所对的圆周角，故∠E＝∠B.所以∠E＝∠C.
12．△ABC的角平分线AD的延长线交它的外接圆于点E.(1)证明：△ABE∽△ADC.(2)若△ABC的面积S＝ AD·AE，求∠BAC的大小．
1．在圆周角定理的证明中，运用了数学中分类讨论和化归的思想以及归纳的证明方法．这个定理是从特殊情况入手研究的，当角的一边过圆心时，得到圆周角与同弧上的圆心角的关系，然后研究当角的一边不经过圆心时，圆周角与同弧上的圆心角之间的关系，在角的一边不经过圆心时，又有两种情况：一是圆心在圆周角内；二是圆心在圆周角外．经过这样分不同情况的讨论，最后得到不论角的一边是否经过圆心，都有定理中的结论成立．在几何里，许多定理的证明，都需要像这样分情况进行讨论，后面还会遇到这种分情况证明的定理．
2．通过圆周角定理的分析、证明，我们可以看到，在几何里讨论问题时，常常从特殊情况入手，因为在特殊情况下问题往往容易解决，如下图中，中间一种情况为圆周角的一边经过圆心，此时∠AOB＝2∠C很容易证明．特殊情况下的问题解决之后，再想办法把一般情况下的问题转化为特殊情况下的问题，如下图左图和右图的情况，通过辅助线，把它们变成中间那样的两个角的和或差，这样利用特殊情况下的结论，便可使一般情况下的结论得证．
3．圆周角定理也可理解成一条弧所对的圆心角是它所对的圆周角的二倍；圆周角的度数等于它所对弧的度数的一半．4．圆周角定理及其推论是进一步推导圆及其他重要性质的理论依据，而且为角的计算，推证角相等、弧相等、弦相等，判定相似三角形、直角三角形等平面几何中常见问题提供了十分简便的方法，学习中要注意体会．