数学六年级下册6.5 不等式及其性质备课课件ppt

这是一份数学六年级下册6.5 不等式及其性质备课课件ppt，共26页。PPT课件主要包含了热身运动，不等式的基本性质，探索猜想，做一做，想一想，探索发现，练一练，试一试，挑战自我，拓展提升等内容，欢迎下载使用。

1、如果a = b,b = c,那么a = c （ ）依据：
下列说法是否正确，并说明理由
2、如果a = b,那么a+3 = b+3（ ）依据：
3、如果a = b，那么3a = 3b 或 （ ） 依据：

猜想：不等式是否也具有传递性？
如果a =b，b = c, 那么a = c
如果a b，b c, 那么a c
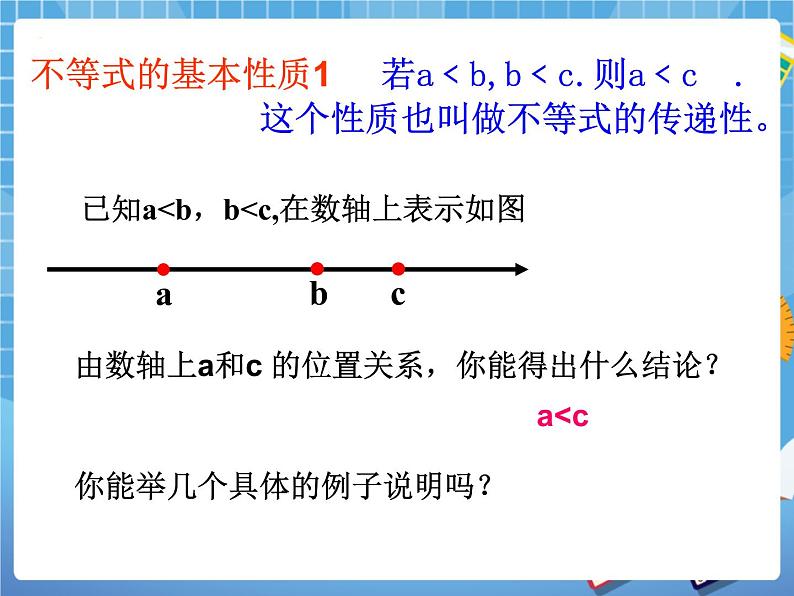
不等式的基本性质1 若a﹤b,b﹤c.则a﹤c . 这个性质也叫做不等式的传递性。
由数轴上a和c 的位置关系，你能得出什么结论？
你能举几个具体的例子说明吗？
猜想：不等式是否也具有类似的性质？
如果a = b，那么a +c= b+ c，a –c= b- c
2.等式的基本性质2:等式的两边都加上（或减去）同一个数 ，等式仍然成立。
如果a＞b，那么a +c＞b+ c，a –c ＞b- c
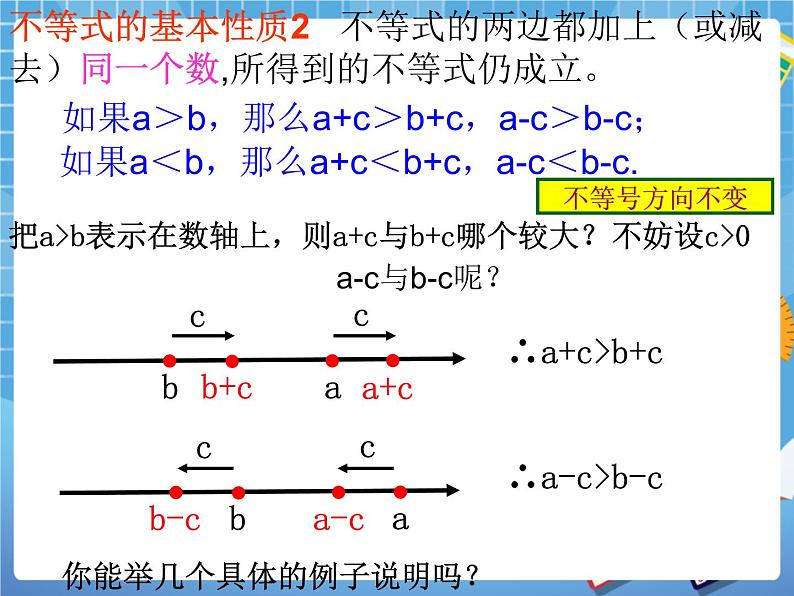
把a>b表示在数轴上，则a+c与b+c哪个较大？
如果a＜b，那么a+c＜b+c，a-c＜b-c.
如果a＞b，那么a+c＞b+c，a-c＞b-c；
不等式的基本性质2 不等式的两边都加上（或减去）同一个数,所得到的不等式仍成立。
2、选择适当的不等号填空，并说明理由.
1、（2010鄂州）根据下图所示，对a、b、c三种物体的质量判断正确的是（ ）
A、ac D、b等式的基本性质3:等式的两边都乘以（或除以）同一个数(除数不能为零)，等式仍然成立。
某同学在完成上题后，归纳认为：不等式的两边都乘以（或除以）同一个数，所得到的不等式仍成立。你认为对吗？为什么？
8＿＿12 8×4＿＿12×4 8÷2＿＿12÷2
8＿＿12 8×(-4)＿＿12×(-4) 8÷(-2)＿＿12÷(-2)
不等式的两边都乘 (或都除以)同一个正数，所得的不等式仍成立； 不等式的两边都乘（或都除以）同一个负数，必须把不等号的方向改变，所得的不等式成立.
即:如果a＞b，且c＞0，那么ac＞bc， ＞ ； 如果a＞b，且c＜0，那么ac＜bc ， ＜ ；
等式的基本性质3 等式的两边都乘以（或除以）同一个数（除数不能为零）, 等式仍成立。
归纳：不等式的基本性质：
性质3：不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立；不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
性质1：若a＜b，b＜c，则a＜c。
性质2：不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
(1)若x+1>0，两边同加上-1， 得_________ (依据：_____________ )；(2)若2x>-6，两边同除以2， 得_________ (依据：_____________ )；(3)若 x≤ ，两边同乘 -3， 得 _________ (依据：________________).
选择适当的不等号,并说明理由（1）已知a>b,则a+1 b+1 （ ）（2）已知a≤b,则-3a -3bb（ ） （3）已知a　如图,在数轴上分别表示2a和a的点(a＜0).2a位于a的左边，所以2a＜a.
例　已知a<0 ，试比较2a与a的大小.
解法一：（不等式的基本性质3）
∵2＞1，a＜0，∴2a＜a.
想一想：还有其他比较2a与a的大小的方法吗？
解法三：（利用不等式基本性质2）
∵a＜0，∴ a+a＜0+a，即2a ＜a.
∵2a－a=a ＜0，∴2a＜a.
判断正误，并说明理由 （1）由5 ﹥ 4，可得5a ﹥ 4a ( ) （2）已知a ﹥ b，可得ac2 ﹥ bc2 ( ) （2）已知ac2 ﹥ bc2 ，可得a ﹥ b ( )
比较等式与不等式的基本性质. 例如：等式是否有与不等式的基本性 质1类似的传递性？ 不等式是否有与等式的基本性质类似的移项法则？你可以用列表的方式进行对比.（请与你的伙伴交流）
若a=b，b=c，则a=c。
若a＜b，b＜c，则a＜c。
如果a＞b,那么a+c＞b+c，a-c＞b-c
如果a=b，那么a+c=b+c，a-c=b-c
等式与不等式的基本性质的区别与联系
通过这节课的学习活动你有哪些收获？
1、不等式的基本性质：
2、学习了三种数学思想方法：类比思想、数形结合思想、分类讨论思想
作业：1、作业本二2、课本p102页的作业题
　　我国于2001年12月11日正式加入世界贸易组织（WTO）。加入前，产品A的进口税超过产品B的进口税的1倍以上；加入后，这两种产品的进口税都下调了15%。你认为加入后产品A的进口税仍超过产品B的进口税的1倍以上吗？请说明理由。
　 解：设加入前产品A、B的进口税分别为a美元、b美元。由题意,得,a>2b。加入后A、B两种产品的进口税分别为（1-15%）a元， （1-15%）b元，由不等式的基本性质3，∵　1-15%＞0∴（1-15%）a＞2 （1-15%）b即表示产品A的进口税仍超过产品B的进口税的1倍以上。
老王和小李在同一家公司工作。老王每月的工资原来比小张要高，但不到他的两倍。新年开始时，公司给他们同时加薪10%，问加薪后老王的工资仍比小张的工资高，但低于两倍吗？请说明理由。如果是每个月各加薪200元呢？