高中数学北师大版必修22.2圆的一般方程学案设计

这是一份高中数学北师大版必修22.2圆的一般方程学案设计，共25页。PPT课件主要包含了圆和圆的位置关系，dR+r，精彩源于发现，注意观察，请你参加，脑筋转转转，你一定能行，试一试等内容，欢迎下载使用。

两个圆没有公共点，并且每个圆上的点都在另一个圆的外部时，叫做这两个圆
两个圆有唯一的公共点，并且除了这个公共点以外，每个圆上的点都在另一个圆的外部时，叫做这两个圆 这个唯一的公共点叫做
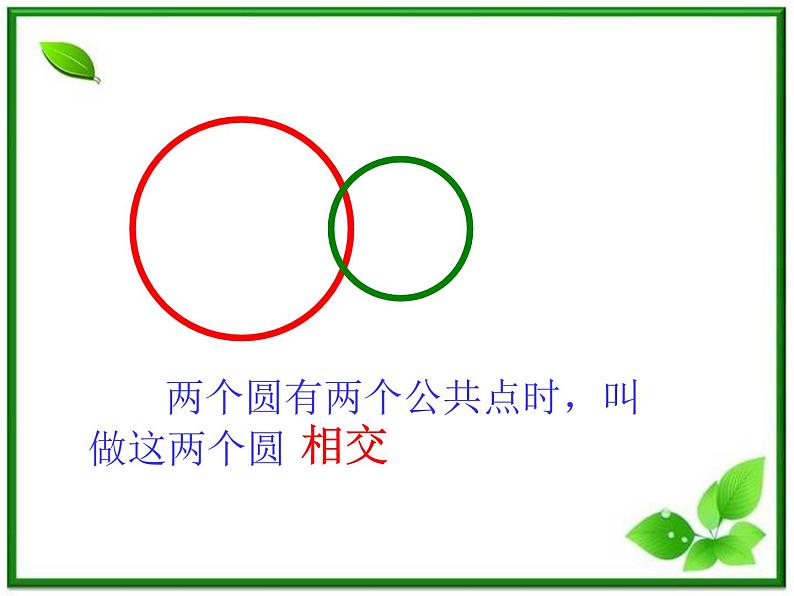
两个圆有两个公共点时，叫做这两个圆
两个圆有唯一的公共点，并且除了这个公共点以外，一个圆上的点都在另一个圆的内部时，叫做这两个圆
两个圆没有公共点，并且一个圆上的点都在另一个圆的内部时，叫做这两个圆
两圆同心是两圆内含的一种特例
想一想：这个图形是不是轴对称图形？
两圆组成的图形是轴对称图形，它们的对称轴是连心线。
如果两个圆相切，那么切点一定在连心线上。
R-rr)
d=R-r (R>r)
dr)
例 如图，OO的半径为5cm，点P是OO外一点，OP=8cm。求（1）以P为圆心作OP与OO外切，小圆OP的半径是多少？（2）以P为圆心作OP与OO内切，大圆OP的半径是多少？
设圆O和圆P的半径分别为R、r，圆心距为d。在下列情况下，两圆的位置关系怎样？
R=6，r=3，d=4
R=6，r=3，d=0
R=3，r=7，d=4
R=5，r=3，d=3
1、若两圆有唯一公共点，且两圆半径分别为5和2，则两圆圆心距为 。
2、 已知，两圆相外切，半径分别是1㎝和2㎝ ，要作和这两个已知圆都相切且半径等于3㎝的圆，可作_____个。
这是一块铁板，上面有A、B、C三个点，经测量，AB=9cm,BC=13cm,CA=14cm,以各顶点为圆心的三个圆两两外切。求各圆的半径。
一个内径3cm的圆钢管在内径为10cm的钢管内沿管壁滚动。
（1）小钢管的圆心与大钢管的圆心的距离是多少？
（2）小钢管的圆心经过的路线是什么？
今有一圆形硬币，在这硬币的周围排列几枚同样大小的硬币，使所有的硬币都与这枚硬币相切，并彼此外切，则需硬币多少枚？
小结：1、两圆的位置关系；
2、圆心距与两圆半径之间的数量关系3、两圆的轴对称性
作业： 1、写一篇数学日记，并解决2—3个问题。 2、课下探究：相交两圆的连心线与公共弦有什么样的结论。