高中数学一轮总复习课件4.1　任意角和弧度制、三角函数的概念

这是一份高中数学一轮总复习课件4.1　任意角和弧度制、三角函数的概念，共37页。PPT课件主要包含了课标要求，备考指导，内容索引，知识筛查，象限角，轴线角，知识巩固，二或第四，-2或-4，π-2等内容，欢迎下载使用。

1.了解任意角的概念和弧度制,能进行弧度与角度的互化,体会引入弧度制的必要性.2.借助单位圆理解三角函数(正弦、余弦、正切)的定义.
本节内容是三角函数的基础,复习时要熟记三角函数的定义、各象限符号值特点以及特殊角的三角函数值,注意角度与弧度的互化.特别地,理解并掌握终边相同的角的集合对于记忆后面三角函数的性质大有好处.
第一环节　必备知识落实
第二环节　关键能力形成
第三环节　学科素养提升
1.任意角(1)定义:角可以看成一条射线绕着它的端点旋转所成的图形.(2)分类:我们规定,一条射线绕其端点按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.如果一条射线没有做任何旋转,就称它形成了一个零角.这样,我们就把角的概念推广到了任意角,包括正角、负角和零角.(3)终边相同的角:所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
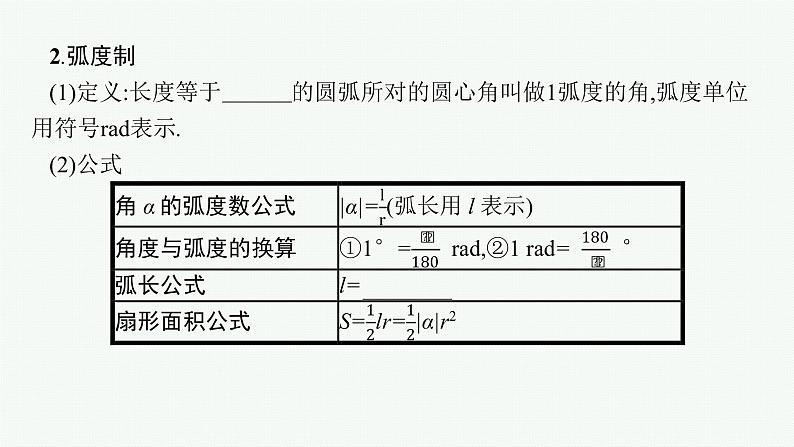
2.弧度制(1)定义:长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度单位用符号rad表示.(2)公式
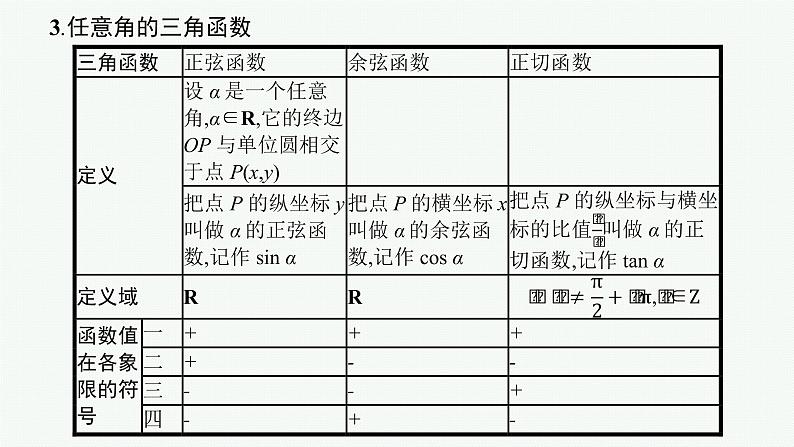
3.任意角的三角函数
4.特殊角的三角函数值
1.下列说法正确的画“√”,错误的画“×”.(1)小于90°的角是锐角.(　　)(2)若sin α>0,则α是第一、第二象限的角.(　　)(3)相等的角的终边一定相同,终边相同的角也一定相等.(　　)(4)锐角是第一象限角,反之亦然.(　　)(5)三角形的内角必是第一、二象限角.(　　)
4.已知角θ的终边经过点P(12,-5),则cs θ的值为　　　　　. 
5.若角θ同时满足sin θ<0,且tan θ<0,则角θ的终边一定落在第　　　象限. 
由sin θ<0,可知θ的终边可能位于第三或第四象限,也可能与y轴的非正半轴重合.由tan θ<0,可知θ的终边可能位于第二象限或第四象限,故θ的终边只能位于第四象限.
(3)已知角α为第三象限角,则2α的终边在　　　　　　　　　　　　　. 
第一或第二象限或y轴的非负半轴
(2)已知角α的终边在直线3x+4y=0上,则5sin α+5cs α+4tan α=　　　　.
解题心得用定义法求三角函数值的两种情况:(1)已知角α终边上一点P的坐标,则直接用三角函数的定义求三角函数值;(2)已知角α的终边所在的直线方程,注意角α的终边位置有两个,对应的三角函数值有两组.
例3　(1)已知扇形的半径为10 cm,圆心角为120°,则扇形的弧长为　　　　　,面积为　　　　　. 
(2)已知扇形的周长为c,则当扇形的圆心角α=　　　　　弧度时,其面积最大,最大面积是　　　　　. 
解题心得求扇形面积的最值常用的思想方法是转化法.一般从扇形面积公式出发,在弧度制下先使问题转化为关于α的函数,再利用基本不等式或二次函数求最值.
对点训练3(1)一个半径为r的扇形,若它的周长等于弧所在的半圆的弧长,则扇形的圆心角是　　　　　弧度,扇形的面积是　　　　　　　　. 
(2)已知在半径为10的圆O中,弦AB的长为10,则弦AB所对的圆心角α的大小为　　　　,α所在的扇形弧长l为　　　　,弧所在的弓形的面积S为　　　　　　. 
审题线路图——挖掘隐含条件寻找等量关系
审题要点1.已知条件:滚动后的圆心坐标为(2,1)和圆的半径为1.2.隐含条件:点P转动的弧长是2.3.等量关系:P转动的弧长等于弧长所对的圆心角.4.解题思路:求点P坐标可借助已知的坐标(2,1),通过构造直角三角形,并在直角三角形中利用三角函数定义可求出.
答案:(2-sin 2,1-cs 2)
解析:如图,作CQ∥x轴,PQ⊥CQ,Q为垂足.