浙教版八年级上册1.5 三角形全等的判定备课课件ppt

这是一份浙教版八年级上册1.5 三角形全等的判定备课课件ppt，共14页。PPT课件主要包含了三个条件，画一画比一比，判定方法3，∴∠A∠D，交流与探索，几何语言，探究新知，应用新知等内容，欢迎下载使用。
(1) 三个角对应相等的两个三角形是全等三角形。
(2)三条边对应相等两个三角形是全等三角形。
全等三角形判定1（SSS）
(3)有两条边和一个角对应相等的两个三角形是全等三角形。
有一个角和夹这个角的两边对应相等的两个三角形是全等三角形。
全等三角形判定2（SAS）
有两边和其中一边的对角对应相等的两个三角形是全等三角形。
(4)有一边和两个角对应相等的两个三角形是全等三角形。
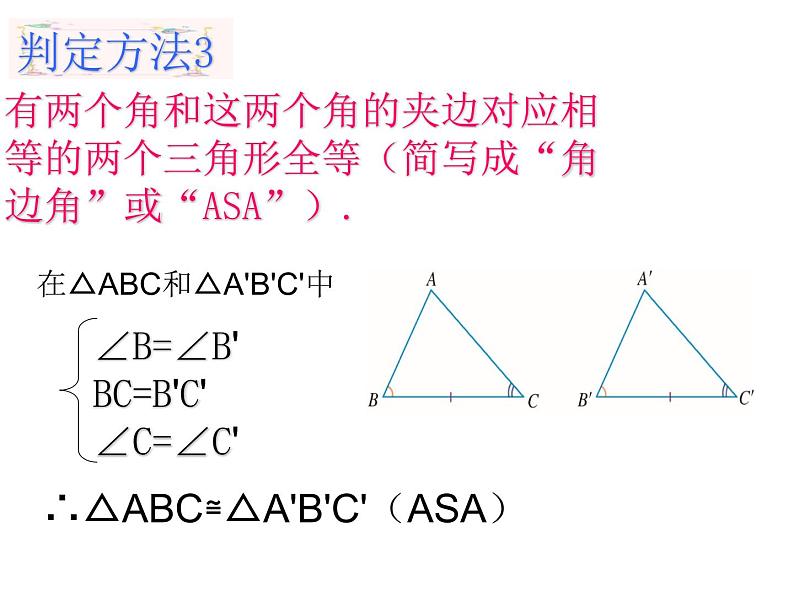
有两个角和这两个角的夹边对应相等的两个三角形是全等三角形。
有两个角和其中一角的对边对应相等的两个三角形是全等三角形。
先画一条3cm的线段，再画一个40°和60°角
由此，你得到了什么结论？
用无刻度的直尺和圆规尺作△ABC，使BC=3cm，∠B=40°，∠C=60°将你画的三角形与其他同学画的三角形比较，你发现了什么？
有两个角和这两个角的夹边对应相等的两个三角形全等（简写成“角边角”或“ASA”）.
在△ABC和△A'B'C'中
∴△ABC≌△A'B'C'（ASA）
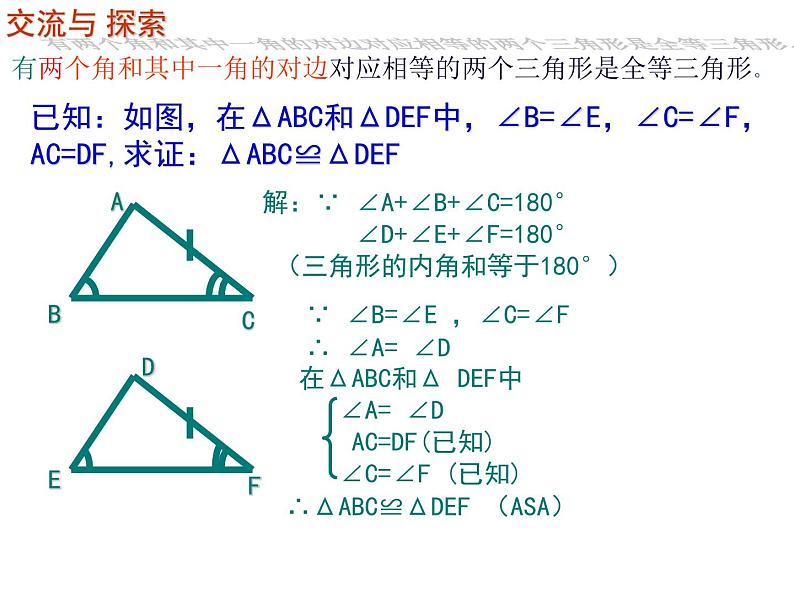
解：∵ ∠A+∠B+∠C=180°　　　 ∠D+∠E+∠F=180° （三角形的内角和等于180°）
已知：如图，在ΔABC和ΔDEF中，∠B=∠E，∠C=∠F，AC=DF,求证：ΔABC≌ΔDEF
∵ ∠B=∠E ，∠C=∠F
在ΔABC和Δ DEF中 ∠A= ∠D AC=DF(已知) ∠C=∠F (已知)
∴ΔABC≌ΔDEF （ASA）
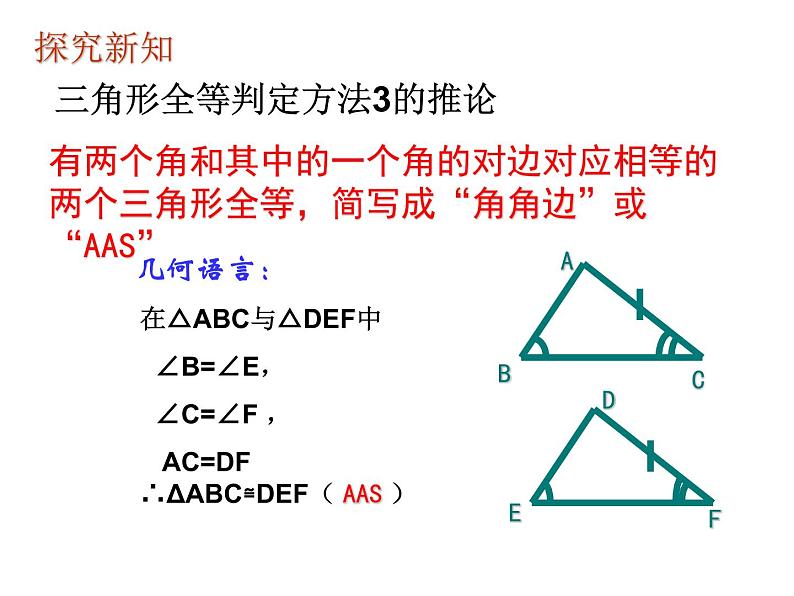
三角形全等判定方法3的推论
在△ABC与△DEF中 ∠B=∠E， ∠C=∠F ， AC=DF ∴ΔABC≌DEF（ AAS ）
有两个角和其中的一个角的对边对应相等的两个三角形全等，简写成“角角边”或“AAS”
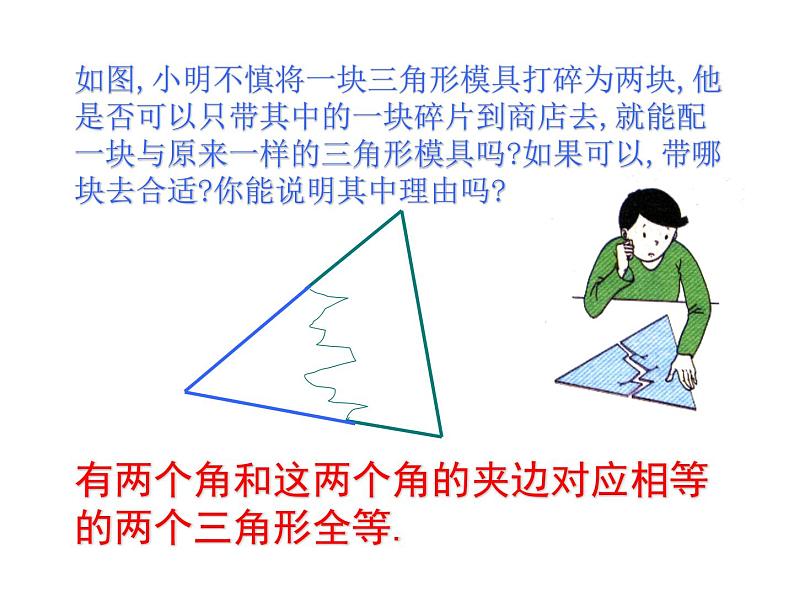
如图,小明不慎将一块三角形模具打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块与原来一样的三角形模具吗?如果可以,带哪块去合适?你能说明其中理由吗?
有两个角和这两个角的夹边对应相等的两个三角形全等.
例4 已知：如图所示，点B,F,E,C在同一条直线上，AB∥CD，且AB=CD,∠A=∠D，求证：AE=DF
例7.如图点P 是∠BAC的平分线上的点（不与点A重合），PB⊥AB,PC⊥AC.说明PB=PC的理由.
角平分线的性质：角平分线上的点到叫角两边的距离相等．
∵P 是∠BAC的平分线上的点， 且PB⊥AB,PC⊥AC ∴PB=PC(角平分线上的点到叫角两边 的距离相等．)
已知：AB∥CD，PB和PC分别平分∠ABC和∠DCB，AD过点P，且与AB垂直。求证:PA=PD
分析：1.已知AB∥CD，AD⊥AB， 可以推出什么？
2.P是∠ABC平分线的点， 那么PA应等于什么？
已知:如图,A,E,F,B 在同一条直线上；CE⊥AB,DF⊥AB,AE＝BF,∠A＝∠B.求证: CE＝DF.