2020-2021学年14.3空间直线与平面的位置关系课文配套ppt课件

这是一份2020-2021学年14.3空间直线与平面的位置关系课文配套ppt课件，共40页。PPT课件主要包含了ABA’B，l⊥m，l⊥mACA’C，ADA’D，CDCD，△ACD≌△A’CD，∠ACE∠A’CE，△ACE≌△A’CE，AEA’E等内容，欢迎下载使用。

一、直线与平面垂直的定义
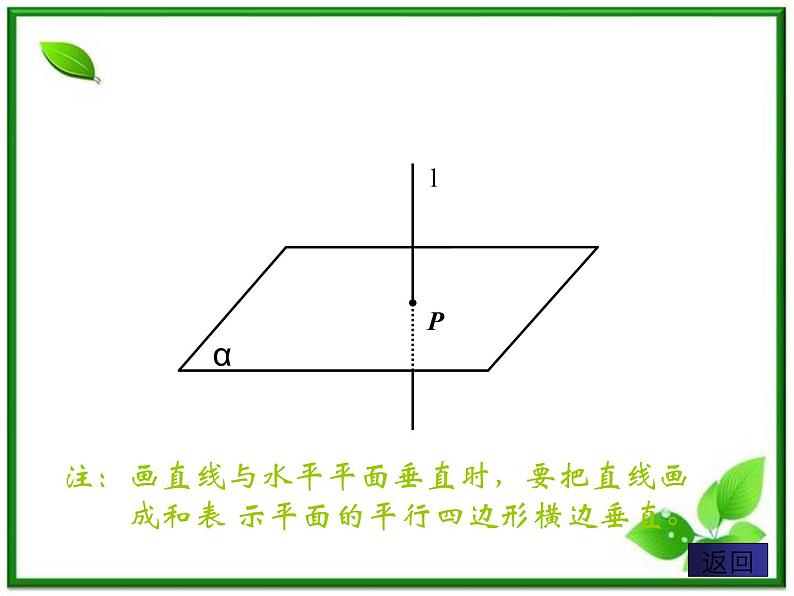
如果一条直线 l 和一个平面α内的任意一条直线都垂直，我们就说直线 l 和平面α互相垂直，记作 l ⊥α。（如图）直线 l 叫做平面α的垂线。平面α叫做直线 l 的垂面。直线 l 和平面α的交点叫做垂足。
注：画直线与水平平面垂直时，要把直线画成和表 示平面的平行四边形横边垂直。
二、直线和平面垂直的判定定理
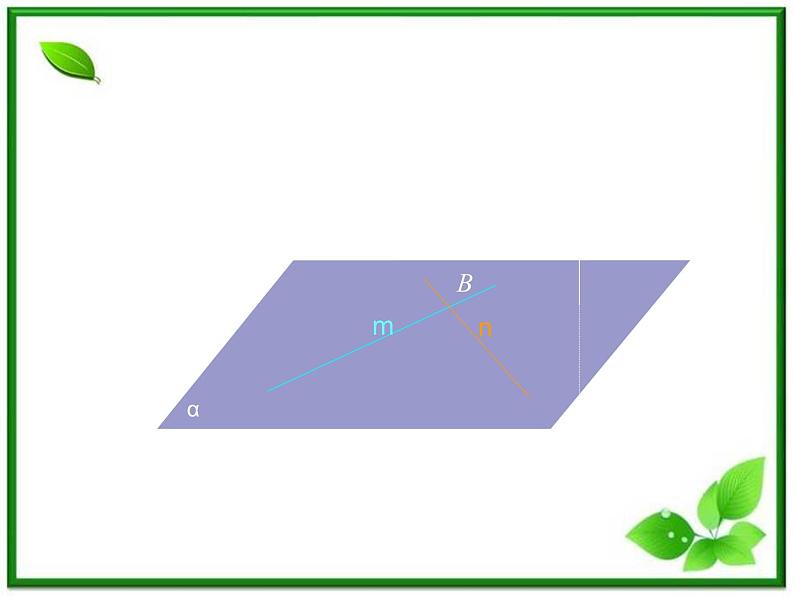
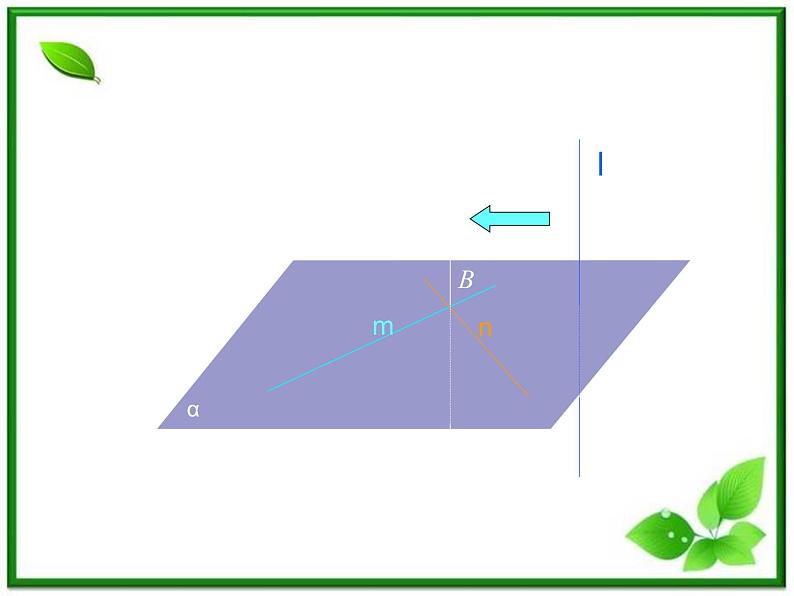
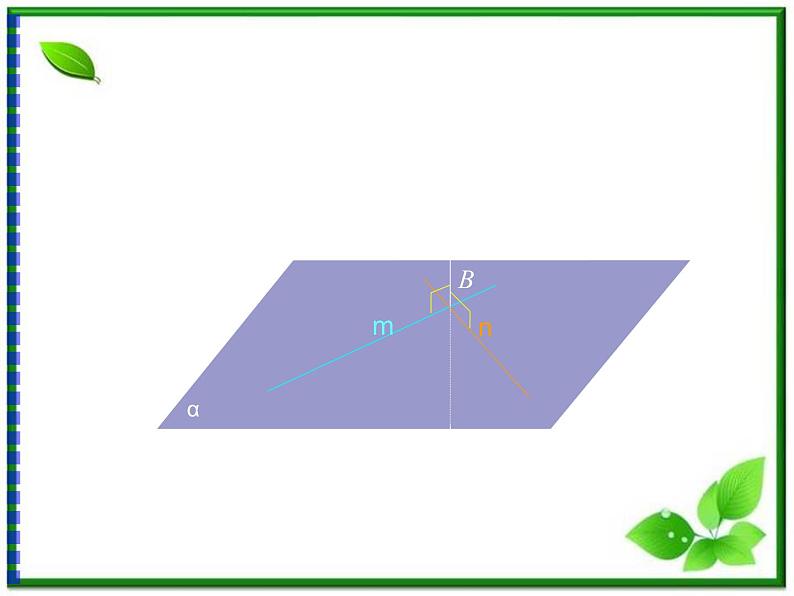
如果一条直线和一个平面内的两条相交直线都垂直，那么这条直线垂直于这个平面。
三、线面垂直判定定理的证明
已知：m  α，n  α，m ∩ n = B，l ⊥ m， l ⊥ n。求证： l ⊥α。
AC=A’CCE=CE
AE=A’EAB=A’B
AE=A’EAB=A’Bl ⊥g
直线和平面垂直的判定定理
这个定理还说明这样一个事实，的确存在着和一个平面内一切直线都垂直的直线，从而得证了直线和平面垂直的合理性。 这个定理不仅提供了判定直线和平面垂值得一种方法，而且还是证明直线和直线互相垂直的一种常用的方法，即要想证明a⊥b，只需证a与b所在平面内的两条相交直线垂直（或证b与a所在平面内的两条相交直线垂直）。
1、如果一条直线垂直于平面内的一条直线，能否判断这条直线和这个平面垂直？2、如果一条直线垂直于平面内的两条直线，能否判断这条直线和这个平面垂直？ 3、如果一条直线垂直于平面内的无数条直线，能否判断这条直线和这个平面垂直？
4、如果三条直线共点、且两两垂直，其中任一条直线是否垂直于另两条直线确定的平面？为什么？5、如果一条直线垂直于一个三角形的两边，能否断定这条直线和三角形的第三条边垂直？为什么？
已知：a∥b，a ⊥α求证：b⊥α
例1 如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于同一个平面。（此定理可看作线面垂直的判定公理二）
证明：在平面α内作两条相交直线m，n ∵ a⊥α ∴ a⊥m ,a⊥n ∵ b∥a ∴ b⊥m ，b⊥n ∴ b⊥α
例2 已知：bα，c  α,b∩c=E， β∩γ=a，c⊥β，d⊥γ。求证：a⊥α。
证明： ∵ b⊥β， β∩γ=a， ∴ b⊥a ； ∵ c⊥γ，β∩γ=a， ∴ c⊥a ； ∵ b∩c=E， bα， cα, ∴ a⊥α。
例3 已知：正方体中，AC是面对角线，BD’是与AC 异面的体对角线。求证：AC⊥BD’
证明： 连接BD ∵正方体ABCD-A’B’C’D’ ∴DD’⊥正方体ABCD ∵AC、BD 为对角线 ∴AC⊥BD ∵DD’∩BD=D ∴AC⊥△D’DB ∴AC⊥BD’