2021-2022学年苏科版八年级数学上册期末复习综合练习题1（word版 含答案）

这是一份2021-2022学年苏科版八年级数学上册期末复习综合练习题1（word版 含答案），共17页。试卷主要包含了下列说法正确的是等内容，欢迎下载使用。
2021-2022学年苏科版八年级数学第一学期期末复习综合练习题1（附答案）
1．在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（　　）
A． B． C． D．
2．下列说法正确的是（　　）
A．﹣27的立方根是3 B．＝±4
C．1的平方根是1 D．4的算术平方根是2
3．在平面直角坐标系的第二象限内有一点M，点M到x轴的距离为3，到y轴的距离为4，则点M的坐标是（　　）
A．（3，﹣4） B．（4，﹣3） C．（﹣4，3） D．（﹣3，4）
4．在等腰三角形ABC中，∠A＝80°．则∠B的度数不可能为（　　）
A．20° B．40° C．50° D．80°
5．如图，已知∠ABC＝∠DCB，下列条件中不能使△ABC≌△DCB的是（　　）

A．AB＝DC B．AC＝DB C．∠1＝∠2 D．∠A＝∠D
6．已知一次函数y＝kx+3的图象经过点A，且y随x的增大而减小，则点A的坐标可以是（　　）
A．（﹣1，2） B．（1，﹣2） C．（2，3） D．（3，4）
7．的平方根是　 　．
8．五峰山大桥位于我市五峰山脚下，是世界运行荷载量最大的高速公铁两用悬索桥，主跨采用1092米钢桁梁悬索桥横跨长江航道，把1092精确到百位，可以表示为 　 　．
9．点A（﹣2，3）关于x轴的对称点A′的坐标为　 　．
10．用三根木棒首尾相连围成一个等腰三角形，其中两根木棒的长度分别为3cm和6cm，则第三根木棒长为 　 　cm．
11．点P（2，﹣4）在正比例函数y＝kx（k是常数，且k≠0）的图象上，则k＝　 　．
12．△ABC的三条边长a、b、c满足c＝8，，则△ABC　 　直角三角形．（填“是”或“不是”）
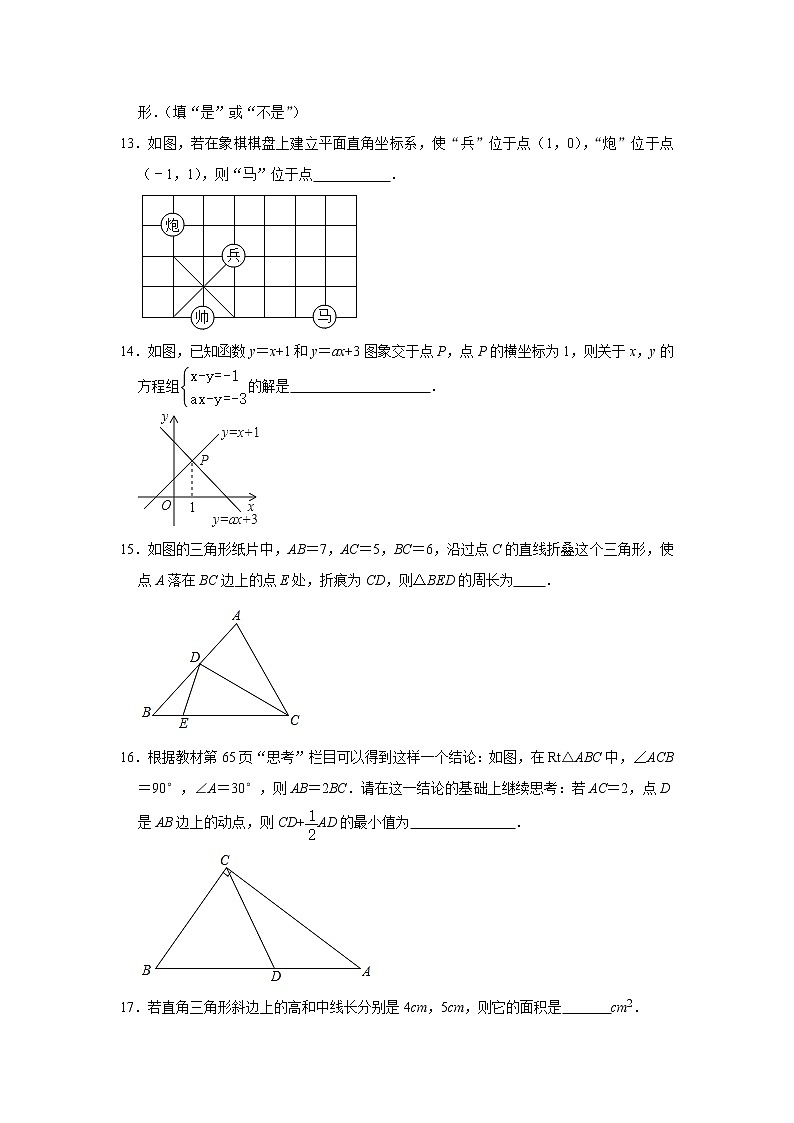
13．如图，若在象棋棋盘上建立平面直角坐标系，使“兵”位于点（1，0），“炮”位于点（﹣1，1），则“马”位于点　 　．

14．如图，已知函数y＝x+1和y＝ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组的解是　 　．

15．如图的三角形纸片中，AB＝7，AC＝5，BC＝6，沿过点C的直线折叠这个三角形，使点A落在BC边上的点E处，折痕为CD，则△BED的周长为　 　．

16．根据教材第65页“思考”栏目可以得到这样一个结论：如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，则AB＝2BC．请在这一结论的基础上继续思考：若AC＝2，点D是AB边上的动点，则CD+AD的最小值为　 　．

17．若直角三角形斜边上的高和中线长分别是4cm，5cm，则它的面积是　 　cm2．
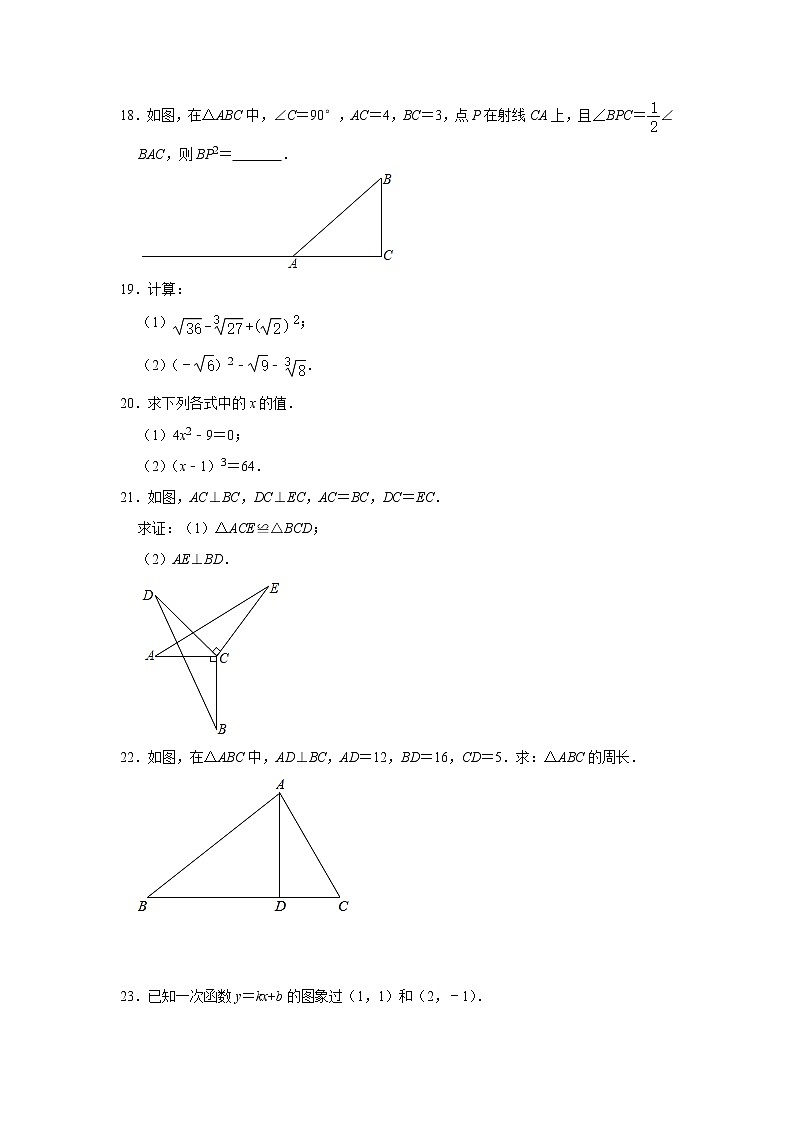
18．如图，在△ABC中，∠C＝90°，AC＝4，BC＝3，点P在射线CA上，且∠BPC＝∠BAC，则BP2＝　 　．

19．计算：
（1）；
（2）（﹣）2﹣﹣．
20．求下列各式中的x的值．
（1）4x2﹣9＝0；
（2）（x﹣1）3＝64．
21．如图，AC⊥BC，DC⊥EC，AC＝BC，DC＝EC．
求证：（1）△ACE≌△BCD；
（2）AE⊥BD．

22．如图，在△ABC中，AD⊥BC，AD＝12，BD＝16，CD＝5．求：△ABC的周长．



23．已知一次函数y＝kx+b的图象过（1，1）和（2，﹣1）．
（1）求一次函数y＝kx+b的解析式；
（2）求直线y＝kx+b与坐标轴围成的三角形的面积．

24．如图，在△ABC中，边AB的垂直平分线OM与边AC的垂直平分线ON交于点O，这两条垂直平分线分别交BC于点D、E．
（1）若∠ABC＝30°，∠ACB＝40°，求∠DAE的度数；
（2）已知△ADE的周长11cm，分别连接OA、OB、OC，若△OBC的周长为27cm，求OA的长．


25．某地区的电力资源缺乏，未能得到较好的开发．该地区一家供电公司为了居民能节约用电，采用分段计费的方法来计算电费．月用电量x（度）与相应电费y（元）之间的函数图象如图所示．
（1）月用电量为50度时，应交电费多少元？
（2）当x≥200时，求y与x之间的函数关系式；
（3）月用电量为150度时，应交电费多少元？


26．某校机器人兴趣小组在如图所示的三角形场地上开展训练．已知：△ABC中，∠C＝90°，AB＝5，BC＝3；机器人从点C出发，沿着△ABC边按C→B→A→C的方向匀速移动到点C停止；机器人移动速度为每秒1个单位，移动至拐角处调整方向需要0.5秒（即在B、A处拐弯时分别用时0.5秒）．设机器人所用时间为t秒时，其所在位置用点P表示（机器人大小不计）．
（1）点C到AB边的距离是　 　；
（2）是否存在这样的时刻，使△PBC为等腰三角形？若存在，求出t的值；若不存在，请说明理由．




27．[定义]
如果1条线段将一个三角形分成2个等腰三角形，那么这1条线段就称为这个三角形的“二分等腰线”，如果2条线段将一个三角形分成3个等腰三角形，那么这2条线段就称为这个三角形的“三分等腰线”．
[理解]
（1）如图（1），在△ABC中，∠A＝33°，∠C＝81°，请你在这个三角形中画出它的“二分等腰线”，不限作法，请在图中标出等腰三角形顶角的度数．
（2）如图（2），已知△ABC是一个顶角为36°的等腰三角形，请你在这个三角形中画出它的“三分等腰线”，不限作法，请在图中标出所分得的等腰三角形底角的度数．
[应用]
（3）小明在学习了上面的材料后得到一个结论：直角三角形一定存在“二分等腰线”；而小丽则认为直角三角形也一定存在“三分等腰线”．
①你认为直角三角形的　 　就是它的“二分等腰线”；
②如图（3），在△ABC中，∠C＝90°，请你在图（3）中帮助小丽画出△ABC的“三分等腰线”（要求：尺规作图，不写作法，保留作图痕迹）．
（4）在△ABC中，∠C＝33°，AD和DE分别是△ABC的“三分等腰线”，点D在BC边上，点E在AB边上，且AD＝DC，BE＝DE，请根据题意写出∠B度数的所有可能的值　 　．




























参考答案
1．解：A、不是轴对称图形，不合题意；
B、不是轴对称图形，不合题意；
C、是轴对称图形，符合题意；
D、不是轴对称图形，不合题意；
故选：C．
2．解：A、﹣27的立方根是﹣3，故本选项错误；
B、＝4，故本选项错误；
C、1的平方根是±1，故本选项错误；
D、4的算术平方根是2，故本选项正确．
故选：D．
3．解：由题意，得
x＝﹣4，y＝3，
即M点的坐标是（﹣4，3），
故选：C．
4．解：当∠A为顶角，
∴∠B＝＝50°；
当∠B是顶角，则∠A是底角，则∠B＝180°﹣80°﹣80°＝20°；
当∠C是顶角，则∠B与∠A都是底角，则∠B＝∠A＝80°，
综上所述，∠B的度数为50°或20°或80°，
故选：B．
5．解：A、在△ABC和△DCB中，
，
∴△ABC≌△DCB（SAS）；故本选项能使△ABC≌△DCB；
B、本选项不能使△ABC≌△DCB；
C、在ABC和△DCB中，
，
∴△ABC≌△DCB（ASA）；故本选项能使△ABC≌△DCB；
D、在△ABC和△DCB中，
，
∴△ABC≌△DCB（AAS）；故本选项能使△ABC≌△DCB．
故选：B．
6．解：A、当点A的坐标为（﹣1，2）时，﹣k+3＝2，
解得：k＝1＞0，
∴y随x的增大而增大，选项A不符合题意；
B、当点A的坐标为（1，﹣2）时，k+3＝﹣2，
解得：k＝﹣5＜0，
∴y随x的增大而减小，选项B符合题意；
C、当点A的坐标为（2，3）时，2k+3＝3，
解得：k＝0，选项C不符合题意；
D、当点A的坐标为（3，4）时，3k+3＝4，
解得：k＝＞0，
∴y随x的增大而增大，选项D不符合题意．
故选：B．
7．解：的平方根是±．
故答案为：±．
8．解：1092精确到百位为：1100＝1.1×103．
故答案为：1.1×103．
9．解：点A（﹣2，3）关于x轴的对称点A′的坐标为（﹣2，﹣3），
故答案为：（﹣2，﹣3）．
10．解：组成等腰三角形的两根木棒的长度分别为3cm和6cm，
根据三角形三边关系可得，组成等腰三角形的第三根木棒长为6cm，
故答案为：6．
11．解：∵点P（2，﹣4）在正比例函数y＝kx（k是常数，且k≠0）的图象上，
∴﹣4＝2×k，
解得：k＝﹣2，
故答案为：﹣2．
12．解：∵，
∴a﹣4＝0，b﹣6＝0，
即a＝4，b＝6，
∵a2+b2＝16+36＝52，c2＝8×8＝64，
∴a2+b2＜c2，
∴△ABC 不是直角三角形，
故答案为：不是．
13．解：建立平面直角坐标系如图所示，
“马”位于点（4，﹣2）．
故答案为：（4，﹣2）．

14．解：把x＝1代入y＝x+1，得出y＝2，
函数y＝x+1和y＝ax+3的图象交于点P（1，2），
即x＝1，y＝2同时满足两个一次函数的解析式．
所以关于x，y的方程组的解是．
故答案为．
15．解：∵△ACD沿着CD翻折得△CDE，
∴AD＝DE，AC＝CE，
∵AC＝5，BC＝6，
∴BE＝BC﹣AC＝6﹣5＝1，
∴△BED的周长为BD+DE+BE＝BA+BE＝8，
故答案为：8．
16．解：作射线AG，使得∠BAG＝30°，
过D作DE⊥AG于E，过C作CF⊥AG于F，

∴DE＝AD，
∴CD+AD＝CD+DE≥CF，
∵∠CAG＝∠CAB+∠BAG＝60°，AC＝2，
∴CF＝，
∴CD+AD的最小值为．
故答案为：．
17．解：∵直角三角形斜边上中线长5cm，
∴斜边＝2×5＝10cm，
∴面积＝×10×4＝20cm2．
故答案为：20．
18．解：如图，连接BP，

∵∠BAC是△ABP的外角，
∴∠BAC＝∠BPC+∠ABP，
∵∠BPC＝∠BAC，
∴∠BPC＝∠ABP，
∴AB＝AP，
在△ABC中，∠C＝90°，
由勾股定理得：AB＝，
∴PA＝AB＝5，
∴PC＝9，
在Rt△BCP中，由勾股定理得：
BP2＝PC2+BC2＝92+32＝90，
故答案为：90．
19．解：（1）原式＝6﹣3+2＝5．
（2）原式＝6﹣3﹣2＝1．
20．解：（1）4x2﹣9＝0，
4x2＝9，
x2＝，
解得x＝±；
（2）（x﹣1）3＝64，
x﹣1＝4，
解得x＝5．
21．（1）证明：∵AC⊥BC，DC⊥EC，
∴∠ACB＝∠DCE＝90°，
∴∠ACB+∠ACD＝∠DCE+∠ACD，
即∠ECA＝∠DCB，
在△ACE和△BCD中，
，
∴△ACE≌△BCD（SAS）；
（2）证明：如图，AC与BD相交于点G，AE与BD相交于点F，

由（1）知，△ACE≌△BCD，
∴∠A＝∠B，
∵∠AGD＝∠BGC，∠B+∠BGC＝90°，
∴∠A+∠AGD＝90°，
∴∠AFG＝180°﹣90°＝90°，
∴AE⊥BD．
22．解：在Rt△ABD和Rt△ACD中，
根据勾股定理得：AB2＝AD2+BD2，AC2＝AD2+CD2，
∴AB＝＝20，AC＝＝13，
∴△ABC的周长＝AB+AC+BC＝AB+AC+BD+DC＝20+13+16+5＝54，即△ABC的周长是54．
23．解：（1）∵一次函数y＝kx+b的图象经过两点A（1，1），B（2，﹣1），
∴，
解得：，
∴一次函数解析式为：y＝﹣2x+3．
（2）∵y＝﹣2x+3与x轴、y轴交点的坐标分别为（，0）、（0，3），
∴与坐标轴围成的三角形的面积S＝×3×＝．
24．解：（1）∵∠ABC＝30°，∠ACB＝40°，
∴∠BAC＝180°﹣∠ABC﹣∠ACB＝180°﹣30°﹣40°＝110°，
∵DM是线段AB的垂直平分线，
∴DA＝DB，
∴∠DAB＝∠ABC＝30°，
同理，EA＝EC，
∴∠EAC＝∠ACB＝40°，
∴∠DAE＝∠BAC﹣∠BAD﹣∠EAC＝110°﹣30°﹣40°＝40°；
（2）连接OA，OB，OC，

∵△ADE的周长11cm
∴AD+DE+EA＝11（cm），
∴BC＝DB+DE+EC＝AD+DE+EA＝11（cm）；
∵△OBC的周长为27cm，
∴OB+OC+BC＝27（cm），
∵BC＝11cm，
∴OB+OC＝16（cm），
∵OM垂直平分AB，
∴OA＝OB，
同理，OA＝OC，
∴OA＝OB＝OC＝8（cm）．
25．解：（1）当0＜x≤100时，设y＝mx，
将（100，60）代入可得：100x＝60，
解得：x＝，
∴当0＜x≤100时，y＝x，
当x＝50时，y＝＝30，
∴月用电量为50度时，应交电费30元；
（2）当x≥200时，设y＝kx+b，
将（100，60），（200，200）代入可得：，
解得：，
∴当x≥2100时，y与x之间的函数关系式为y＝x﹣80；
（3）当x＝150时，y＝，
即月用电量为150度时，应交电费130元．
26．解：（1）△ABC中，∠C＝90°，
∴AB2＝AC2+BC2，
∵AB＝5，BC＝3，
∵52＝AC2+32，
∴AC＝4，
∴点C到AB边的距离＝＝＝2.4；
故答案为：2.4；
（2）存在，使△PBC为等腰三角形时，P在AB上或在AC上，
当P在AB上时，
①BC＝BP，
∵BP＝t﹣0.5﹣3，
∴t﹣0.5﹣3＝3，
解得：t＝6.5；
②CB＝CP，如图1，
过点C作CD⊥AB于D，则BD＝PD，

由（1）知：CD＝2.4，
∵BC＝3，
∴BD＝＝1.8，
∴BP＝3.6，
∴t＝3.6+3+0.5＝7.1；
③PB＝CP，
∴∠B＝∠PCB，
∵∠ACP+∠PCB＝∠A+∠B＝90°，
∴∠ACP＝∠A，
∴AP＝CP＝BP＝2.5，
∴t＝2.5+0.5+3＝6；
当P在AC上，CB＝CP＝3，
∴t＝3+5+0.5+0.5+4﹣3＝10．
综上所述，t的值为6.5或7.1或6或10．
27．解：（1）如图（1）中，线段CD即为所求；

（2）如图（2）中，线段AE，BF即为所求；

（3）①你认为直角三角形的斜边上的中线就是它的“二分等腰线”；
故答案为：斜边上的中线．
②如图（3），线段BE，CT即为所求；

（4）设∠B＝x，
①当AD＝DE时，如图1（a），
∵AD＝CD，
∴∠C＝∠CAD＝33°，
∵DE＝EB，
∴∠B＝∠EDB＝x，
∴∠AED＝∠DAE＝2x，
∴33°×2+2x+x＝180°，
∴x＝38°，
∴∠B＝38°；

②当AD＝AE时，如图1（b），
∵AD＝CD，
∴∠C＝∠CAD＝33°，
∵DE＝EB，
∴∠B＝∠EDB＝x，
∴∠AED＝∠ADE＝2x，
∴2x+x＝33°+33°，
∴x＝22°，
∴∠B＝22°．

③当EA＝DE时，
∵90°﹣x+33°+33°+x＝180°，
∴x不存在，应舍去．
综合上述：∠B的度数的所有可能值为38°或22°，
故答案为：38°或22°．