



人教版新课标A必修51.2 应用举例教课ppt课件
展开2、 大角对大边,小角对小边 .
(1)已知三边,求三个角;
(2)已知两边和它们的夹角,求第三边和其它两角;
(3)判断三角形的形状。
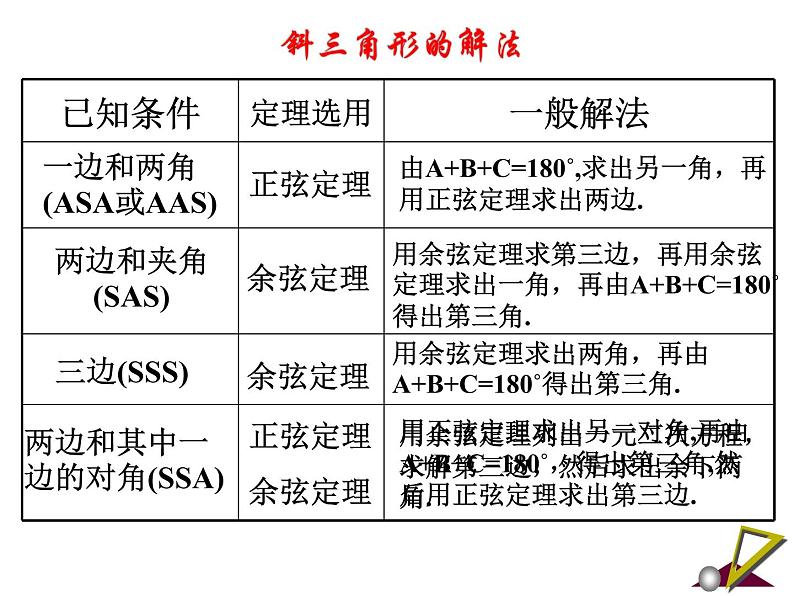
用正弦定理求出另一对角,再由A+B+C=180˚,得出第三角,然后用正弦定理求出第三边.
由A+B+C=180˚,求出另一角,再用正弦定理求出两边.
用余弦定理求第三边,再用余弦定理求出一角,再由A+B+C=180˚得出第三角.
用余弦定理求出两角,再由A+B+C=180˚得出第三角.
一边和两角(ASA或AAS)
两边和其中一边的对角(SSA)
用余弦定理列出一元二次方程,求解第三边,然后求出余下两角.
(1)坡度:斜面与地平面所成的角度.
(2)仰角和俯角:在视线和水平线所成的角中,视线在水平线上方的角叫仰角,视线在水平线下方的角叫俯角.
(3)方位角:从正北方向顺时针转到目标方向的夹角.
(4)视角:由物体两端射出的两条光线在眼球内交叉而成的角.
解斜三角形中的有关名词、术语:
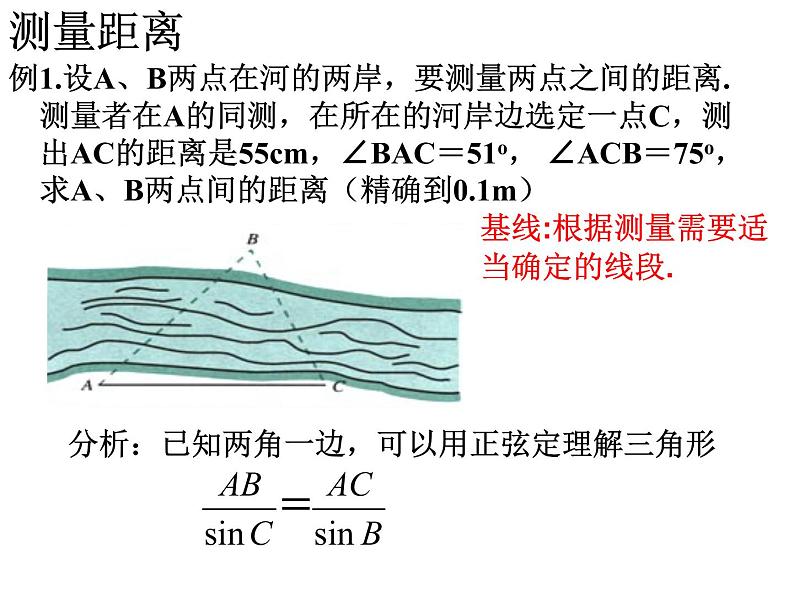
例1.设A、B两点在河的两岸,要测量两点之间的距离.
测量者在A的同测,在所在的河岸边选定一点C,测出AC的距离是55cm,∠BAC=51, ∠ACB=75,求A、B两点间的距离(精确到0.1m)
分析:已知两角一边,可以用正弦定理解三角形
基线:根据测量需要适当确定的线段.
例6 一艘海轮从A出发,沿北偏东75°的方向航行67.5n mile后到达海岛B,然后从B出发,沿北偏东32°的方向航行54.0n mile后到达海岛C.如果下次航行直接从A出发到达C,此船应该沿怎样的方向航行,需要航行多少距离(角度精确到0.1°,距离精确到0.01n mile)?
人教A版 (2019)必修 第二册第六章 平面向量及其应用6.4 平面向量的应用图片课件ppt: 这是一份人教A版 (2019)必修 第二册第六章 平面向量及其应用6.4 平面向量的应用图片课件ppt,共60页。PPT课件主要包含了余弦定理的推导,平方的,积的两倍,反思感悟,已知三边解三角形,注意点,随堂演练,设第三条边长为x,直角三角形,课时对点练等内容,欢迎下载使用。
湘教版(2019)必修 第二册1.7 平面向量的应用举例完美版课件ppt: 这是一份湘教版(2019)必修 第二册1.7 平面向量的应用举例完美版课件ppt,共30页。PPT课件主要包含了学习目标,新知学习,典例剖析,课堂小结等内容,欢迎下载使用。
人教A版 (2019)必修 第二册6.4 平面向量的应用课文配套ppt课件: 这是一份人教A版 (2019)必修 第二册6.4 平面向量的应用课文配套ppt课件,共12页。PPT课件主要包含了kmh,课堂小结等内容,欢迎下载使用。













