2021-2022学年北师大版八年级数学上册期中模拟训练题B卷（word版含答案）

期中考试模拟训练题B卷

考试时间：90分钟；总分：120

一、单选题（将唯一正确答案的代号填在题后括号内，每题3分，共36分）

1．下列变量之间的关系不是函数关系的是（    ）

A．长方形的宽一定，其长与面积 B．正方形的周长与面积

C．等腰三角形的底边与面积 D．速度一定时，行驶的路程与时间

2．在Rt△ABC中，，三边是a、b、c，则以下结论正确的是（    ）．

A． B． C． D．以上答案都不对

3．如果一次函数的图象经过一、二、四象限，则k的取值范围是（    ）

A． B． C． D．

4．计算等于（   ）

A． B． C． D．

5．下列计算正确的是（    ）

A． B． ﹣ ＝1

C．×＝ D．

6．如图，四个实数m，n，p，q在数轴上对应的点分别为M，N，P，Q，若n＋q＝0，则m，n，p，q四个实数中，绝对值最大的一个是（    ）

A．p B．q C．m D．n

7．以下说法中，正确的个数有（    ）

（1）在坐标轴上的点横坐标、纵坐标都是零；

（2）点P(2，﹣3)到x轴的距离为3；

（3）三角形的三条高都在三角形内部；

（4）平分三角形内角的射线叫三角形的角平分线．

A．1 B．2 C．3 D．4

8．两个一次函数y1＝ax+b与y2＝bx+a（a，b为常数，且ab≠0），它们在同一个坐标系中的图象可能是（　　）

A． B． 

C． D．

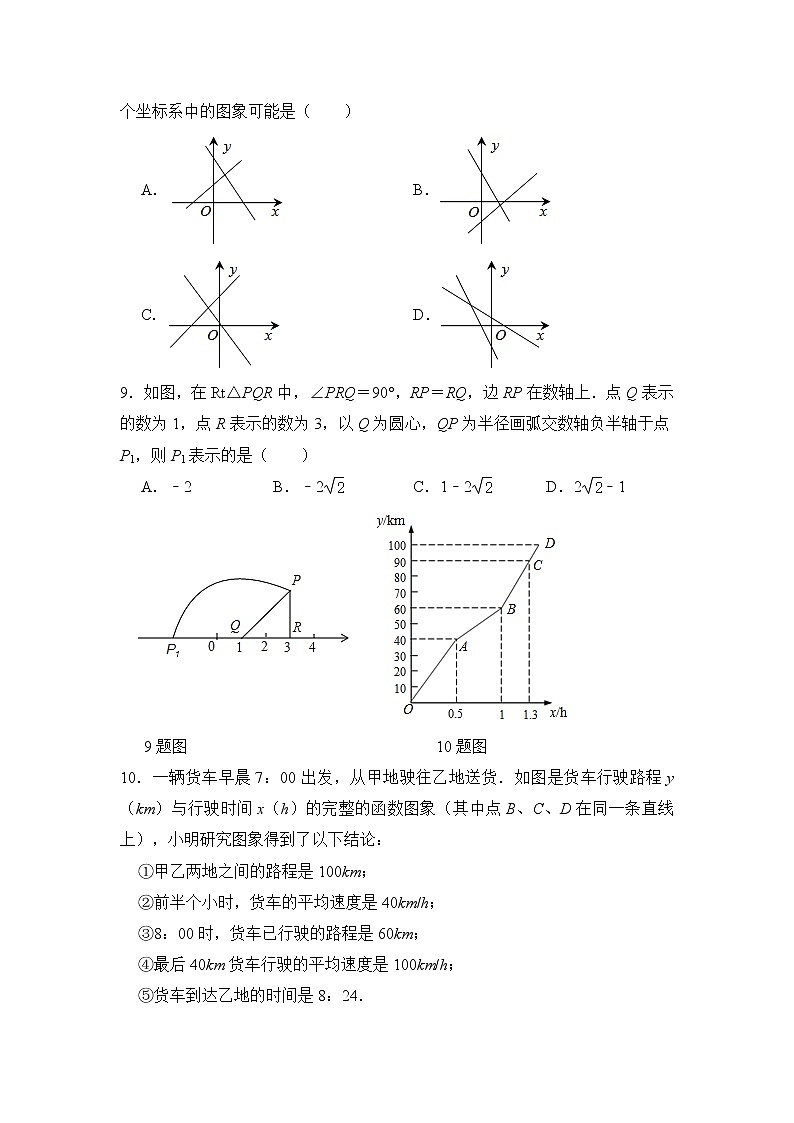
9．如图，在Rt△PQR中，∠PRQ＝90°，RP＝RQ，边RP在数轴上．点Q表示的数为1，点R表示的数为3，以Q为圆心，QP为半径画弧交数轴负半轴于点P1，则P1表示的是（　　）

A．﹣2 B．﹣2 C．1﹣2 D．2﹣1

   9题图                               10题图

10．一辆货车早晨7：00出发，从甲地驶往乙地送货．如图是货车行驶路程y（km）与行驶时间x（h）的完整的函数图象（其中点B、C、D在同一条直线上），小明研究图象得到了以下结论：

①甲乙两地之间的路程是100km；

②前半个小时，货车的平均速度是40km/h；

③8：00时，货车已行驶的路程是60km；

④最后40km货车行驶的平均速度是100km/h；

⑤货车到达乙地的时间是8：24．

其中，正确的结论是（　　）

A．①②③④ B．①③⑤ C．①③④ D．①③④⑤

11．如图，平面直角坐标系中，已知点，，，，动点P从点A出发，以每秒2个单位的速度按逆时针方向沿四边形ABCD的边做环绕运动；另一动点Q从点C出发，以每秒3个单位的速度按顺时针方向沿四边形CBAD的边做环绕运动，则第2020次相遇点的坐标是（    ）

A． B． C． D．

   11题图                                   12题图

12．如图，直线y＝x+2与x轴、y轴分别交于点A和点B，点C、D分别为线段AB、OB的中点，点P为OA上一动点，PC+PD值最小时点P的坐标为（　　）

A．（﹣，0） B．（﹣，0） C．（﹣，0） D．（﹣，0）

二、填空题（将正确答案填在题中横线上，每题3分，共24分）

13．若点在y轴上，则点P关于x轴对称的点为__________．

14．当x=-1时，代数式x2+2x+2的值是__________．

15．比较大小：3_____4．

16．如果线段能组成一个直角三角形，那么________组成直角三角形．(填“能”或“不能”)．

17．如图所示，有一块直角三角形纸片，两直角边AB＝6，BC＝8，将直角边AB折叠使它落在斜边AC上，折痕为AD，则BD＝______．

18．在一个长为13米，宽为8米的矩形草地上，如图堆放着一根长方体的木块，它的棱长和场地宽AD平行且大于AD，木块的正视图是边长为1米的正方形，一只蚂蚁从点A处，到达C处需要走的最短路程是________米．

       17题图                              18题图

19．如果将点（﹣b，﹣a）称为点（a，b）的“反称点”，那么点（a，b）也是点（﹣b，﹣a）的“反称点”，此时，称点（a，b）和点（﹣b，﹣a）是互为“反称点”．容易发现，互为“反称点”的两点有时是重合的，例如（0，0）的“反称点”还是（0，0）．请再写出一个这样的点：　　．

20．如图，在一单位为1的方格纸上，△A1A2A3，△A3A4A5，△A5A6A7……都是斜边在x轴上，斜边长分别为2，4，6……的等腰直角三角形，若△A1A2A3的顶点坐标分别为A1（2，0），A2（1，﹣1），A3（0，0），则依图中所示规律，A2020的坐标为　   　．

三、解答题（本题共有8小题，共60分）

21．（本题6分）计算：   

（1） ；   

（2）[a3⋅a5+（3a4）2]÷a2 ．

22．（本题6分）已知实数，，在数轴上所对应的点的位置如图所示，化简：．

23．（本题6分）已知蜡烛燃烧时长度的变化与时间成正比例关系，一根长为的蜡烛点燃6分钟后，蜡烛变短了，设蜡烛点燃x分钟后变短了．

（1）求函数y关于自变量x的解析式，并写出自变量的取值范围；

（2）画出此函数的图象．

24．（本题8分）如图是一台雷达探测相关目标得到的结果，若记图中目标C的位置为，则其余各目标的位置分别是多少？

25．（本题8分）在直角坐标系中，已知直线交x轴于点A，交y轴于点B，直线上的点在第一象限内，设的面积是S．

（1）写出S与m之间的函数关系式，并写出m的取值范围；

（2）当S=3时，求点P的坐标；

（3）若直线OP平分的面积时，求点P的坐标．

26．（本题8分）观察下列等式：

第一个等式：

第二个等式：

第三个等式：，

…

请回答下列问题：

（1）则第四个等式为______．

（2）用含（为正整数）的式子表示出第个等式为______．

27．（本题8分）如图（1），是两个全等的直角三角形（直角边分别为a，b，斜边为c）．

（1）用这样的两个三角形构造成如图（2）的图形（B，E，C三点在一条直线上），利用这个图形，求证：a2+b2＝c2

（2）当a＝1，b＝2时，将其中一个直角三角形放入平面直角坐标系中（如图（3）），使直角顶点与原点重合，两直角边a，b分别与x轴、y轴重合．

①请在坐标轴上找一点C，使△ABC为等腰三角形．

写出一个满足条件的在x轴上的点的坐标：　  　；

写出一个满足条件的在y轴上的点的坐标：　  　，这样的点有　  　个．

28．（本题10分）如图，在等腰Rt△ABC中，AB＝AC，D为斜边BC的中点E，F分别为AB、AC边上的点，且DE⊥DF，若BE＝8，CF＝6．

（1）判断△DEF的形状，并说明理由；

（2）求△DEF的面积．

期中考试模拟训练题B卷参考答案

1．C. 解析：长方形的宽一定，其长与面积，符合函数定义，故不符合题意；

正方形的周长与面积，符合函数定义，故不符合题意；

等腰三角形的底边与面积，在这个变化过程中，还有底边上的高是变量，所以不符合函数定义，故符合题意；

速度一定时，行驶的路程与时间，符合函数定义，故不符合题意；

故选：

2．A. 解析：∵在中，，的三边是a、b、c，

∴斜边为b，∴，故选：A．

3．D. 解析：如果一次函数的图象经过第一、二、四象限，
则解得-1＜k＜0．故选：D．

4．A. 解析：

=.

故选：A．

5．C. 解析：A选项错误，不是同类二次根式不可以加减；

B选项错误，不是同类二次根式不可以加减；

C选项正确；

D选项错误，．

故选：C．

6．A. 解析：∵n＋q＝0，

∴n和q互为相反数，0在线段NQ的中点处，

∴绝对值最大的点P表示的数p，

故选A．

7．A. 解析：（1）在轴上的点横坐标为0，纵坐标不一定为0，轴上的点的纵坐标都是0，横坐标不一定为0，坐标原点的横坐标、纵坐标都为0，故（1）的说法错误；

（2）点P（，）到轴的距离为，故（2）的说法正确；

（3）锐角三角形的三条高都在三角形内部，直角三角形有两条高为直角边，一条高在三角形内部，钝角三角形有两条高在三角形外部，一条高在三角形内部，故（3）说法错误；

（4）平分三角形内角的射线与对边相交，其顶点与对边交点之间的线段叫三角形的角平分线．故（4）的说法错误；

故选：A．

8．解：A、可知：a＞0，b＞0．

∴直线经过一、二、三象限，故A错误；

B、可知：a＜0，b＞0．

∴直线经过一、二、四象限，故B正确；

C、∵ab≠0，故直线不经过原点，故C错误；

D、可知：a＜0，b＞0，

∴直线经过一、三、四象限，故D错误．

故选：B．

9．解：QP＝＝＝2，

∵Q表示1，∴P1表示的是1﹣2，故选：C．

10．解：①由图象可知到达D点货车到达乙地了，

∴甲乙两地之间的路程是100km；

②由图象可知，x＝0.5时y＝40，

∴货车的平均速度是40÷0.5＝80km/h；

③当x＝1时，y＝60，

∴8：00时，货车已行驶的路程是60km；

④由图可知B（1，60），C（1.3，90），

∴货车在BC段行驶的速度为v＝＝100km/h；

⑤从C点到D点行驶的路程是100﹣90＝10km，

∴时间为＝0.1h，

∴从C点到D点行驶的时间为0.1h，

∴货车到达乙地的总行驶时间为1.3+0.1＝1.4，

∴货车到达乙地的时间是8：24；

∴①③④⑤正确，

故选：D．

11．B. 解析：∵，，，，

∴，，即，

∴经过1秒钟时，P与Q在处相遇，接下来两个动点运动的路程和为10的倍数时，两点会相遇，

∴第2次相遇在CD的中点，

第3次相遇在，

第4次相遇在，

第5次相遇在，

第6次相遇在，

每五次相遇为一个循环周期，

∵，

∴第2020次相遇点的坐标与第5次相遇点的坐标重合，即，

故选：B．

12．解：作点D关于x轴的对称点D′，连接CD′交x轴于点P，此时PC+PD值最小，如图．

令y＝x+2中x＝0，则y＝2，

∴点B的坐标为（0，2）；

令y＝x+2中y＝0，则x+2＝0，解得：x＝﹣3，

∴点A的坐标为（﹣3，0）．

∵点C、D分别为线段AB、OB的中点，

∴点C（﹣，1），点D（0，1）．

∵点D′和点D关于x轴对称，

∴点D′的坐标为（0，﹣1）．

设直线CD′的解析式为y＝kx+b，

∵直线CD′过点C（﹣，1），D′（0，﹣1），

∴有，解得：，

∴直线CD′的解析式为y＝﹣x﹣1．

令y＝0，则0＝﹣x﹣1，解得：x＝﹣，

∴点P的坐标为（﹣，0）．

故选：A．

13．. 解析：∵点P（−2a，a−1）在y轴上，
∴−2a＝0，解得：a＝0，∴点P坐标为（0，−1），
∴点P关于x轴对称的点的坐标为（0，1），
故答案为：（0，1）．

14．6. 解析：当时，

故答案为：6．

15．＜. 解析：（1）＝45，（4）2＝48，

∵45＜48，∴3＜4．故答案为：＜．

16．能. 解析：设c为斜边，则由勾股定理得：

，两边同乘以，得，即 ，

根据勾股定理的逆定理可得能组成直角三角形．

故答案为：能

17．3. 解析：∵△ABC为直角三角形，AB=6，BC=8，

∴根据勾股定理得：，

设BD=x，由折叠可知：ED=BD=x，AE=AB=6，∠A=∠AED=90°

可得：CE=AC-AE=10-6=4，CD=BC-BD=8-x，∠DEC=90°

在Rt△CDE中，

根据勾股定理得：（8-x）2 =42+x2，

解得：x=3，则BD=3．

故答案为:3．

18．17. 解析：由题意可知，将木块展开，相当于是AB+2个正方形的宽，

∴长为13+1×2=15米；宽为8米

于是最短路径为： (米)．

故答案为：17．

19. （3，﹣3）. 解析：根据题意可得这样的点是（3，﹣3），

故答案为：（3，﹣3）；

20. （2，1010）．解：∵各三角形都是等腰直角三角形，

∴直角顶点的纵坐标的长度为斜边的一半，

A2（1，﹣1），A4（2，2），A6（1，﹣3），A8（2，4），A10（1，﹣5），A12（2，6），…，

∵2020÷4＝505，

∴点A2020在第一象限，横坐标是2，纵坐标是2020÷2＝1010，

∴A2020的坐标为（2，1010）．

故答案为：（2，1010）．

21．（1）解：原式＝2+4+1+3＝10；

（2）解：原式＝（a8+9a8）÷a2＝10a8÷a2＝10a6；

22．解：由数轴可得：，，，

则原式

．

23．解：（1）设，把点（6，3.6）代入得：，

解得，

∴函数y关于自变量x的解析式为：，自变量的取值范围为：；

（2）列表如下：

函数图像如下所示：

24．解： 图中目标C的位置为，

目标A的位置为，目标B的位置为，

目标D的位置为，目标E的位置为，

25．解：（1）∵直线交轴于点，交轴于点，

∴，，∵，

，∴，

∵点在第一象限内，

∴，

解得：；

（2）当时，，解得：，

此时，

∴点P的坐标为；

（3）若直线平分的面积，则点为的中点，

∵，，∴点的坐标为．

26．解：（1）根据题中式子规律可得

（2）．

27. 解：（1）由图可得，×（a+b）（a+b）＝ab+c2+ab，

整理得＝，

∴a2+2ab+b2＝2ab+c2，∴a2+b2＝c2．

（2）一个满足条件的在x轴上的点的坐标：（﹣1，0）；

一个满足条件的在y轴上的点的坐标：（0，2+），这样的点有 4个．

故答案为：（﹣1，0）；（0，2+），4．

28. 解：（1）连接AD，

∵AB＝AC，D为BC的中点，

∴AD⊥BC，AD＝CD＝BD，∠DAE＝45°＝∠C，

∵DE⊥DF，∴∠CDF+∠ADF＝∠EDA+∠ADF，

即∠CDF＝∠ADE，

在△DCF和△ADE中，

，

∴△DCF≌△ADE（ASA），

∴DF＝DE，

又∵DE⊥DF，

∴△DEF为等腰直角三角形；

（2）由△DCF≌△ADE可得：AE＝CF＝6，

∴AF＝BE＝8．

∵∠EAF＝90°，

∴EF2＝AE2+AF2＝62+82＝100，

又∵△DEF为等腰直角三角形，

∴DE2+DF2＝EF2＝100，即2DE2＝100，

∴DE2＝50，

∴S△DEF＝×DE×DF＝×DE2＝25．