初中数学青岛版九年级上册2.1 锐角三角比教案

锐角三角比

一、教与学目标：

1.通过实验、观察、探究、交流、猜想等数学活动，探索锐角三角比的意义.

2.能叙述锐角三角比的概念，记住三角比的符号，让学生能说出锐角三角比的文字语言与符号语言.

3.会求直角三角形中指定锐角的三角比.

二、教与学重点难点：

重点：探索锐角三角比的意义.

难点：求直角三角形中指定锐角的三角比.

三、教与学方法：

   自主探究、合作交流

四、教与学过程：

（一）知识回顾

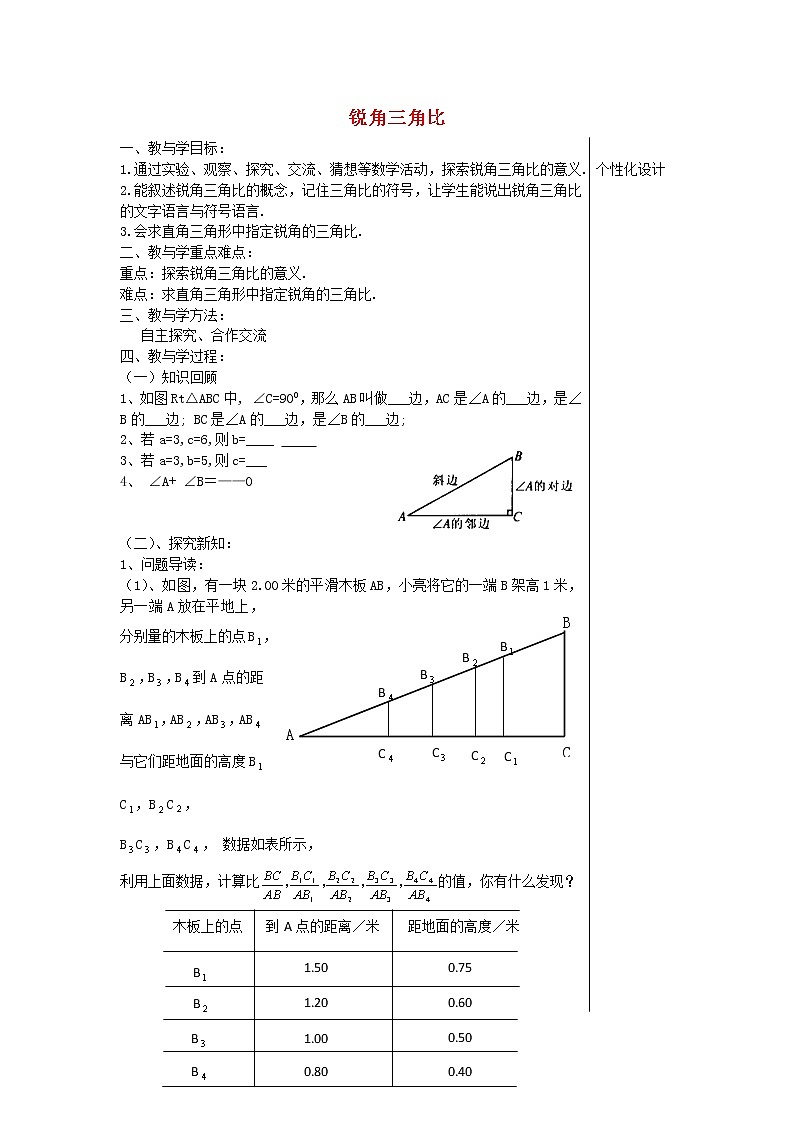
1、如图Rt△ABC中, ∠C=900，那么AB叫做___边，AC是∠A的___边，是∠B的___边; BC是∠A的___边，是∠B的___边;

2、若a=3,c=6,则b=____     

3、若a=3,b=5,则c=___

4、 ∠A+ ∠B＝——0

（二）、探究新知：

1、问题导读：

（1）、如图，有一块2.00米的平滑木板AB，小亮将它的一端B架高1米，另一端A放在平地上，分别量的木板上的点B，B，B，B到A点的距离AB，AB，AB，AB与它们距地面的高度BC，BC，

BC，BC， 数据如表所示，

利用上面数据，计算比的值，你有什么发现？

个性化设计

（2）、如图9-2（1），作一个锐角A，在∠A的一边上任意取两个点B,B′,经过这两个点分别向∠A的另一边作垂线，垂足分别为C，C′，比值相等吗?为什么？

（3）、如果设，那么对于确定的锐角A来说，比值K的大小与

点B′在AB边上的位置有关吗？

（4）、如图9-2（2），以点A为端点，在锐角A的内部作一条射线，在这条射线上取点B″，使AB″=AB′,这样又得到了一个锐角∠CAB″.过B″作B″C″⊥AC，垂足为C″.比与K的值相等吗？为什么？由此你得到怎样的结论？

2、合作交流：三角比的定义

在Rt△ABC中，如果锐角A确定，那么∠A的对边与斜边的比、邻边与斜边的比也随之确定.

∠A的对边与斜边的比叫做∠A的正弦(sine)，记作sinA，

即sinA＝

∠A的邻边与斜边的比叫做∠A的余弦(cosine)，记作cosA，

即cosA=

∠A的对边与∠A的邻边的比叫做∠A的正切(tangent)，记作tanA，

即

锐角A的正弦、余弦和正切统称锐角A的三角比.

注意：sinA，cosA，tanA都是一个完整的符号，单独的 “sin”没有意义，其中A前面的“∠”一般省略不写.

3、精讲点拨：

 在Rt△ABC，∠C=90°，把∠A的对边记作a, 把∠B的对边记作b, 把

个性化设计

∠C的对边记作c,你能分别用a，b，c表示∠A的正弦、余弦和正切吗？

sinA＝，cosA=，tanA=

仿照如此，你能分别用a，b，c表示∠B的正弦、余弦和正切吗？

例1：（课本64页，图略）如图,在Rt△ABC中,∠C=90°，AC=4,BC=2, 求∠A的正弦,余弦和正切的值.

分析：由勾股定理求出AB的长度，再根据直角三角形中锐角三角比与三边之间的关系求出各函数值.

生：独立思考，交流结果，举手板演． 

（三）、学以致用：

1、巩固新知：

（1）、在△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边，下列关系式中错误的是（  ）

    A．b=c cosB    B．b=a tanB    C．a=c sinA    D．a=b cosB

（2）、在△ABC中，∠C=90°，AB=2，AC=1，则Sin B的值是（    ）

A.        B.      C.     D.2

（3）、如图，已知正方形ABCD的边长为2，如果将线段BD绕着点B旋转后，点D落在CB的延长线上的D′处，那么tan∠BAD′等于（     ）      

A．1       B．      

C．    D．

2、能力提升：

（1）、如果是锐角，且，那么的值是（ ）．

A.               B.       C.                D.

（2）、在⊿ABC中，∠C = ，∠A，∠B，∠C的对边分别是，，，且，则；；；

（四）、达标测评：

1、选择题：

（1）、直角三角形的两条边长分别为3、4，则第三条边长为  (    )A．5    B．7    C．    D．5或

（2）、如图，在Rt△ABC中，∠C＝90°，

个性化设计

BC＝4，AC＝3，CD⊥AB于D，设∠ACD＝a，则cos的值为    (    )

A．  B．   C．   D．

2、填空题：

（3）、在△ABC中，∠C=90°，若4a=5b，则sinA=_____，cosA=_____，tanA=_______．

（4）、在⊿ABC中，∠C = ，若则；

3、解答题：

（5）、在Rt△ABC中，∠C = ，BC=8，sinA＝，求cosA和tanB的值.

（6）、在Rt△ABC中，∠C = ，AB=2AC, 求cosB和tanA的值.

五、课堂小结：

在RtΔABC中,设∠C=900，∠α为RtΔABC的一个锐角，则

∠α的正弦 ， ∠α的余弦 ，

∠α的正切.

六、作业布置：

必做题：习题2.1 A组，

选做题: 习题2.1 B组