初中数学湘教版七年级下册2.2.2完全平方公式教学ppt课件

这是一份初中数学湘教版七年级下册2.2.2完全平方公式教学ppt课件，共18页。PPT课件主要包含了学习目标，知识回顾，方法一，直接求，方法二，间接求，情境引入，p2+2p+1，m2+4m+4，p2－2p+1等内容，欢迎下载使用。

1.理解并掌握完全平方公式的推导过程、结构特点;（重点）2.会运用公式进行运算；(难点)
平方差公式 ( a + b )( a – b )=a2 - b2
那么(a+b)(a+b)和(a-b)(a-b)是否也能用一个公式来表示呢？
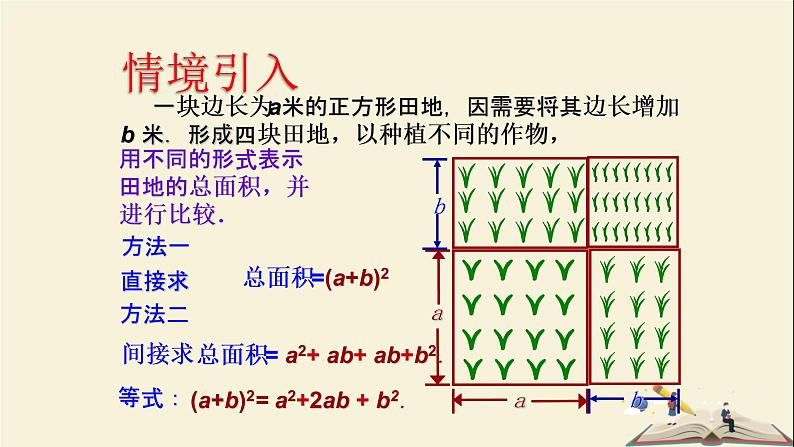
一块边长为a米的正方形田地，因需要将其边长增加 b 米．形成四块田地，以种植不同的作物，
用不同的形式表示田地的总面积，并进行比较．
总面积=(a+b)2
总面积= a2+ ab+ ab+b2．
(a+b)2= a2+2ab + b2．
计算下列多项式的积，你能发现什么规律？
（1） （p+1)2=(p+1)(p+1)= .
（2） （m+2)2=(m+2)(m+2)= .
（3） （p－1)2=(p－1)(p－1)= .
（4） （m－2)2=(m－2)(m－2)= .
根据上面的规律，你能直接下面式子的写出答案吗？
(a＋b)2= .
(a－b)2= .
两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍.这两个公式叫作完全平方公式.
简记为：“首平方，尾平方， 积的 2倍放中间”
2.积中的两项为两数的平方；
3.另一项是两数积的2倍，且与乘式中间的符号相同.
4.公式中的字母a，b可以表示数，单项式和多项式.
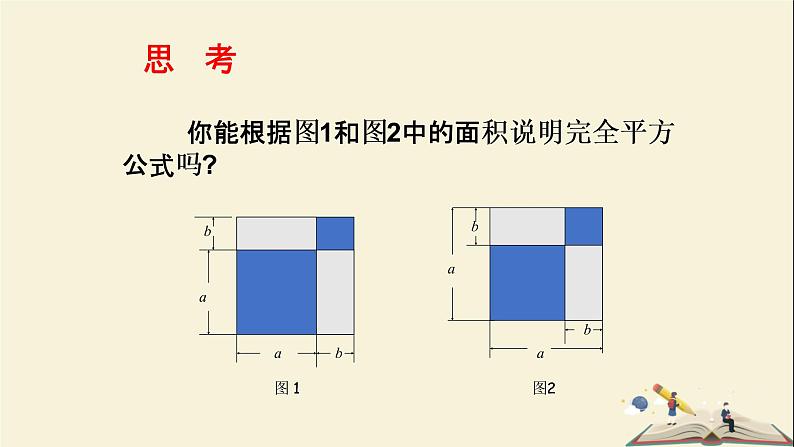
你能根据图1和图2中的面积说明完全平方公式吗?
完全平方公式 的几何意义
( 2x + y )2
( + )2
= ( )2 + · ( )· + 2
= 4x2+4xy+y2，
= a 2 + 2 · a · b + b 2 .
可以用类似的方法直接得到(2x-y)2的结果吗？
你能利用完全平方公式快速地计算出(2x+y)2吗？
(a+b)2=a2+2ab+b2.
把2x与y分别看成上式的a与b，也就是把它们按下面的方法对应起来，就可以直接得到结果.
（1）(3m+n)2；
= (3m)2+2 · 3m · n + n2
= 9m2+6mn+n2.
例1.运用完全平方公式计算：
例2 如果36x2＋(m＋1)xy＋25y2是一个完全平方式，求m的值．
解：∵36x2＋(m＋1)xy＋25y2 ＝(±6x)2＋(m＋1)xy＋(±5y)2， ∴(m＋1)xy＝±2·6x·5y， ∴m＋1＝±60， ∴m＝59或－61.
1. 下面各式的计算对不对？如果不对，应怎样改正？
（1）(x+2)2 = x2+4；
（2）(-a-b)2 = a2-2ab+b2.
不对，应是：x2+4x+4；
不对；应是：a2+2ab+b2；
(3) (x -y)2 =x2 -y2；
不对，应是：x2 -2xy+y2
（4）(x+y)2 = x2+xy+y2.
不对，应是：x2 +2xy+y2
（3）若2a2-2ab+b2-2a+1=0则a、b分别（ ）
A．1，-1 B．1，1 C．-1，1 D． 0，0
（4）已知x=a+2b，y=a-2b，求：x2 +xy+y2．
解： x2 +xy+y2=(a+2b)2＋（a＋2b）（a-2b）＋(a-2b)2=(a2＋4ab＋4b2) +(a2－4b2) +(a2－4ab＋4b2)=3a2＋ 4b2
A．4 B．-4 C．0 D．4或-4
（1）已知(a+b)2 = 21， (a-b)2 =5，则ab=( )
A．14 B．9 C．10 D．11