华师大版八年级上册第13章 全等三角形13.3 等腰三角形2 等腰三角形的判定课文课件ppt

这是一份华师大版八年级上册第13章 全等三角形13.3 等腰三角形2 等腰三角形的判定课文课件ppt，共12页。PPT课件主要包含了BAD，CAD，它是真命题吗等内容，欢迎下载使用。

1、等腰三角形是怎样定义的？
有两条边相等的三角形,叫做等腰三角形。
①等腰三角形是轴对称图形。
③等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称为“三线合一”)，它们所在的直线就是等腰三角形的对称轴。
②等腰三角形的两个底角相等(简写成“等边对等角”) 。
2、等腰三角形有哪些性质？
如图，在△ABC中， AB=AC时，
(1) ∵AD⊥BC，∴∠____= ∠____，___= ___.
(2) ∵AD是中线，∴___⊥___ ，∠____ =∠____.
(3) ∵AD是角平分线，∴___ ⊥___ ，____ =____.
几何语言：∵AB=AC(已知) ∴∠B=∠C (等边对等角)
对于命题〝等腰三角形的两个底角相等〞.请先把它改写成〝如果…那么…〞的形式,然后说出它的逆命题.
逆命题:如果一个三角形有两个角相等，那么这个三角形是等腰三角形.
如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
操作一：请在纸上任意画线段BC，分别以点B和点C为顶点，以BC为一边，在BC的同侧画两个相等的角，两角的终边相交于点A。
此时△ABC中，保证了什么条件成立？
操作二：量一量，线段AB与AC的长度。
你发现了什么结论？其他同学的结果与你的相同吗？
如果一个三角形有两个角相等，那么这个三角形是等腰三角形。
（1）已知什么？需要说明的结论是什么？
（2）要说明两条边相等，我们已经有哪些经验？
（3）怎样添加一条辅助线，把△ABC分成两个全等的三角形？
（4）添加顶角的平分线AD，你能说明△ABD与△ACD全等吗？根据什么？
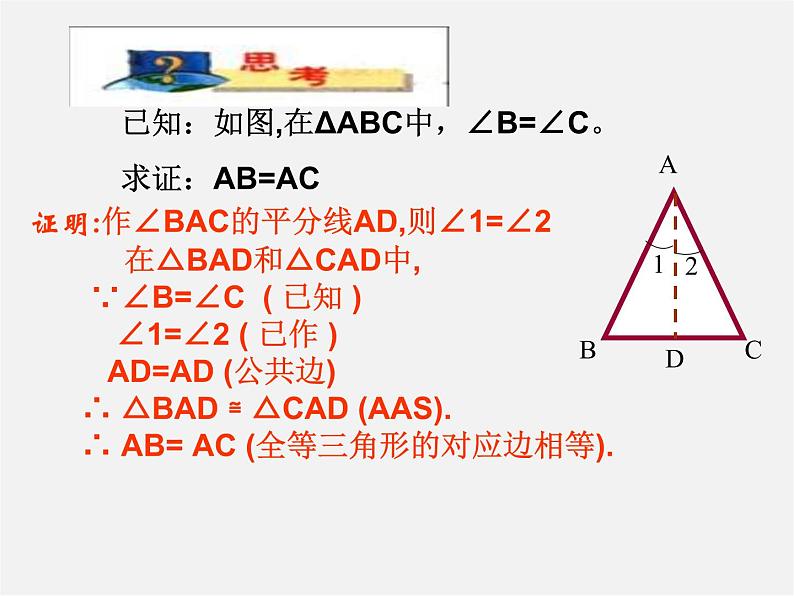
已知：如图,在ΔABC中，∠B=∠C。求证：AB=AC
证明:作∠BAC的平分线AD,则∠1=∠2 在△BAD和△CAD中, ∵∠B=∠C ( 已知 ) ∠1=∠2 ( 已作 ) AD=AD (公共边) ∴ △BAD ≌ △CAD (AAS). ∴ AB= AC (全等三角形的对应边相等).
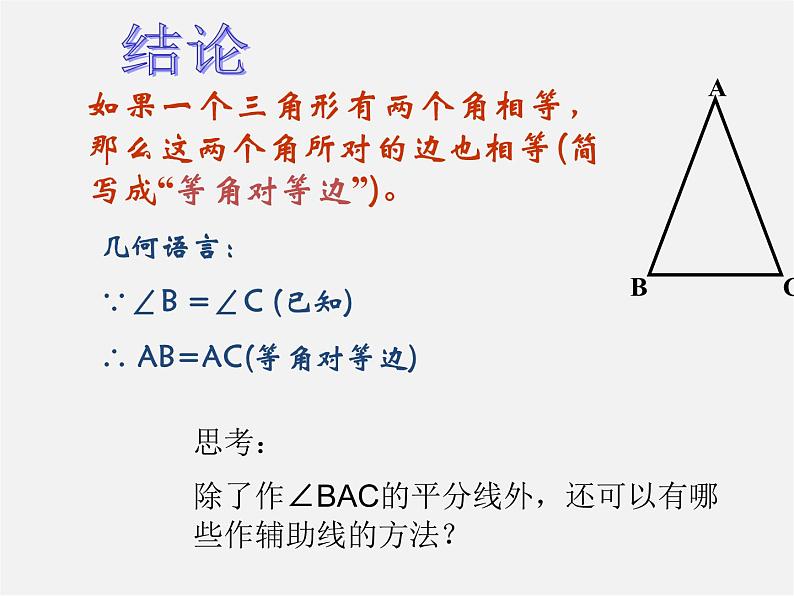
如果一个三角形有两个角相等，那么这两个角所对的边也相等(简写成“等角对等边”)。
几何语言： ∵∠B =∠C (已知) ∴ AB=AC(等角对等边)
思考：除了作∠BAC的平分线外，还可以有哪些作辅助线的方法？
例：如果三角形一个角的外角的角平分线平行于三角形的第三边，那么这个三角形是等腰三角形吗？为什么？
解：∠CAB是ΔABC的外角，AD∥BC， ∴∠1=∠B ∠2=∠C ∴∠B=∠C ∴AB=AC，即ΔABC是等腰三角形
例2：如图,上午10 时，一条船从A处出发以20海里每小时的速度向正北航行，中午12时到达B处，从A、B望灯塔C，测得∠NAC=40°， ∠NBC=80°求从B处到灯塔C的距离
解：∵∠NBC=∠A+∠C∴∠C=80°- 40°= 40° ∴ BA=BC（等角对等边）∵AB=20（12-10）=40∴BC=40答：B处到达灯塔C40海里
1、如图，∠A=36°，∠DBC=36°，∠C=72°。分别计算∠1、∠2的度数，并说明图中有哪些等腰三角形。
2、如图，把一张矩形的纸沿对角线折叠，重合部分是一个等腰三角形吗？
3、如图，AC和BD相交于点O，且AB∥DC，OA=OB。求证：OC=OD。
∠1=72°，∠2=36°
等腰三角形有：△ABC，△ABD， △BCD。
5、已知：如图，AD ∥BC，BD平分∠ABC。求证：AB=AD
证明：∵ AD ∥BC ∴∠ADB=∠DBC ∵ BD平分∠ABC ∴∠ABD=∠DBC ∴∠ABD=∠ADB ∴AB=AD
4、已知：如图，CD是等腰直角三角形ABC斜边上的高，找出图中有哪些等腰直角三角形。
等腰直角三角形有： △ABC ，△ACD ，△BCD。
有两边相等的三角形是等腰三角形
1.两腰相等
运用等腰三角形的判定定理时，应注意在同一个三角形中.