初中数学华师大版八年级上册2 等腰三角形的判定作业ppt课件

这是一份初中数学华师大版八年级上册2 等腰三角形的判定作业ppt课件，共33页。

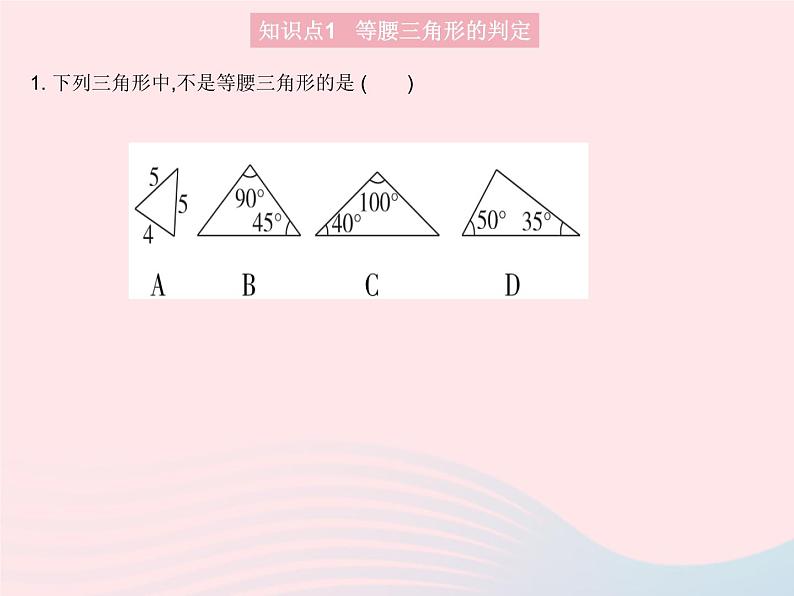
1. 下列三角形中,不是等腰三角形的是 (　　)
知识点1 等腰三角形的判定
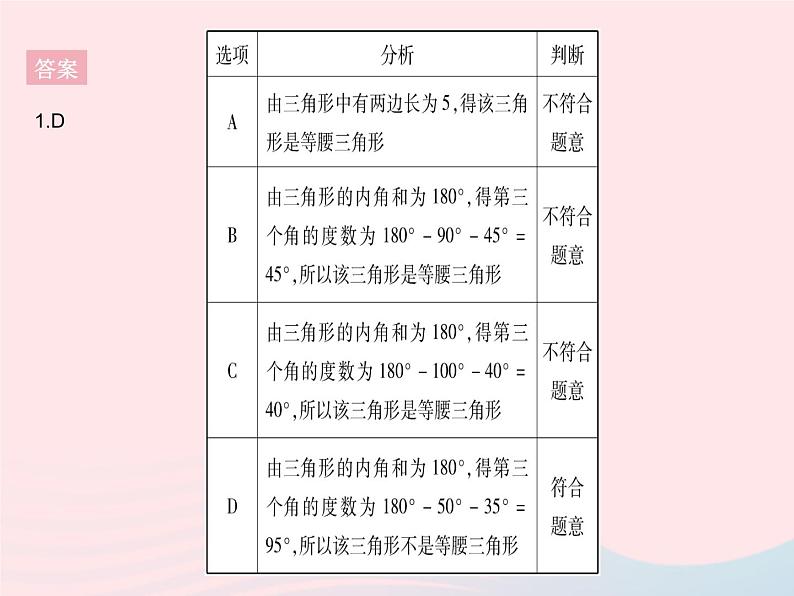
2. 如图,∠BAC=100°,∠B=40°,∠D=20°,AB=3,则CD= (　　)A.2B.2.5C.3D.3.5
2.C　∵∠BAC=100°,∠B=40°,∴∠ACB=180°-∠BAC-∠B=40°,∴AC=AB=3.∵∠D=20°,∴∠CAD=∠ACB-∠D=20°,∴CD=AC=3.
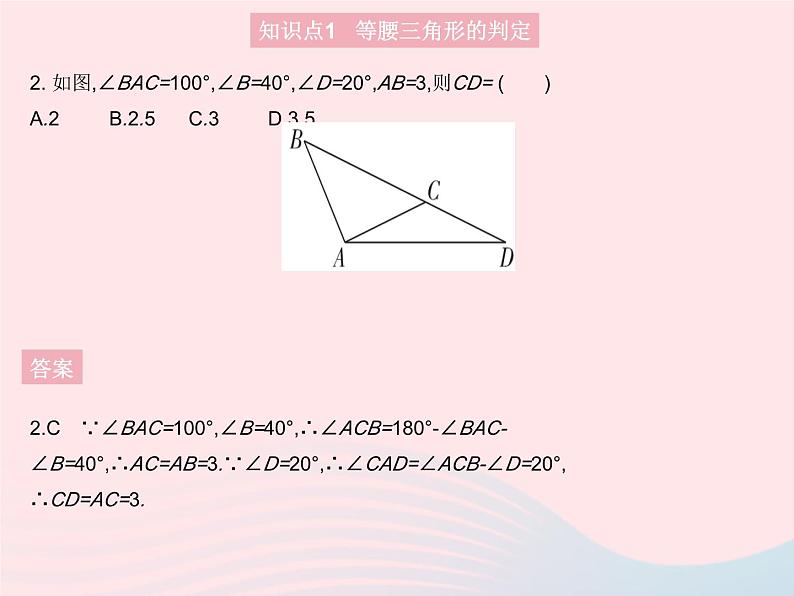
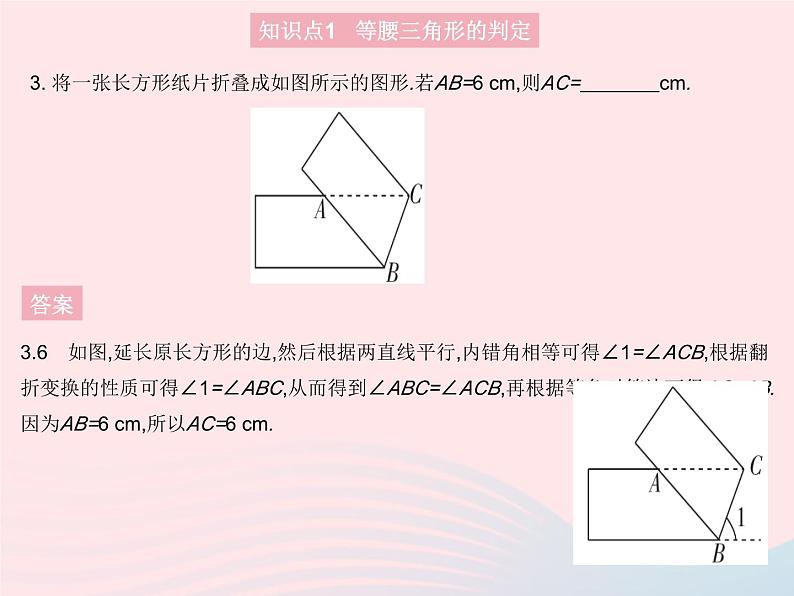
3. 将一张长方形纸片折叠成如图所示的图形.若AB=6 cm,则AC=　　　　cm. 
3.6　如图,延长原长方形的边,然后根据两直线平行,内错角相等可得∠1=∠ACB,根据翻折变换的性质可得∠1=∠ABC,从而得到∠ABC=∠ACB,再根据等角对等边可得AC=AB.因为AB=6 cm,所以AC=6 cm.
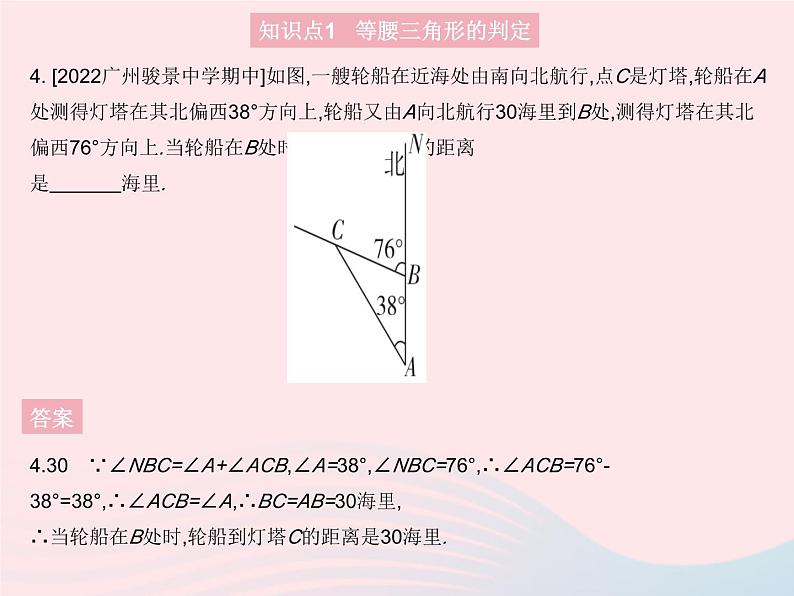
4. [2022广州骏景中学期中]如图,一艘轮船在近海处由南向北航行,点C是灯塔,轮船在A处测得灯塔在其北偏西38°方向上,轮船又由A向北航行30海里到B处,测得灯塔在其北偏西76°方向上.当轮船在B处时,轮船到灯塔C的距离是 海里. 
4.30　∵∠NBC=∠A+∠ACB,∠A=38°,∠NBC=76°,∴∠ACB=76°-38°=38°,∴∠ACB=∠A,∴BC=AB=30海里,∴当轮船在B处时,轮船到灯塔C的距离是30海里.
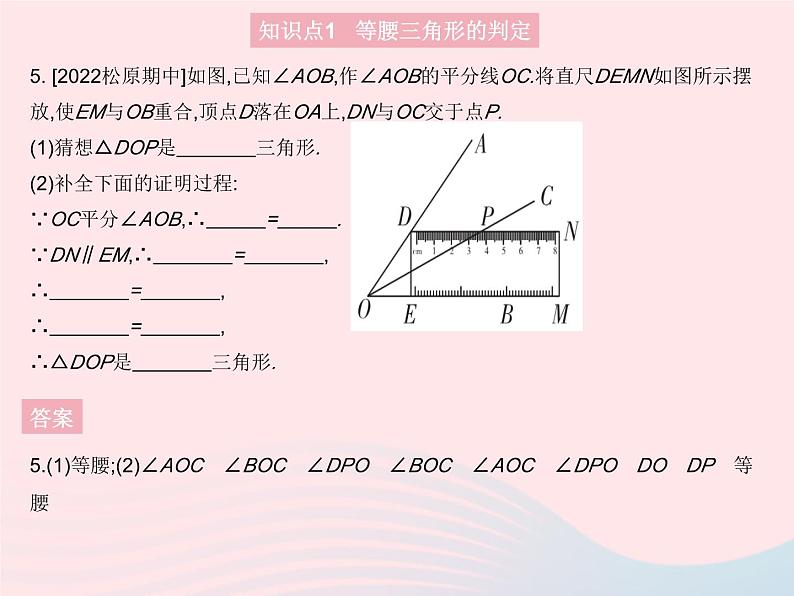
5. [2022松原期中]如图,已知∠AOB,作∠AOB的平分线OC.将直尺DEMN如图所示摆放,使EM与OB重合,顶点D落在OA上,DN与OC交于点P.(1)猜想△DOP是　　　　三角形. (2)补全下面的证明过程:∵OC平分∠AOB,∴　　　=　　　. ∵DN∥EM,∴　　　　=　　　　, ∴　　　　=　　　　, ∴　　　　=　　　　, ∴△DOP是　　　　三角形. 
5.(1)等腰;(2)∠AOC　∠BOC　∠DPO　∠BOC　∠AOC　∠DPO　DO　DP　等腰
6. [2020广东中考]如图,在△ABC中,点D,E分别是AB,AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F.求证:△ABC是等腰三角形.
6.证明:在△BDF与△CEF中,∵∠DBF=∠ECF(已知),∠BFD=∠CFE(对顶角相等),BD=CE(已知),∴△BDF≌△CEF(),∴BF=CF(全等三角形的对应边相等),∴∠FBC=∠FCB(等边对等角),∴∠ABE+∠FBC=∠ACD+∠FCB,∴∠ABC=∠ACB,∴AB=AC(等角对等边),∴△ABC是等腰三角形.
7. [2020宜昌中考改编]如图,在一个池塘两旁有一条笔直小路(B,C为小路端点)和一棵小树(A为小树位置).测得的相关数据为∠ABC=60°,∠ACB=60°,BC=48 米,则AC= (　　)A.45 米B.48 米C.50 米D.52 米
知识点2 等边三角形的判定
7.B　∵∠ABC=60°,∠ACB=60°,∴△ABC是等边三角形,∴AC=BC=48米.
8. 如图,在△ABC中,∠BAC=120°,AD平分∠BAC交BC于点D,DE∥AB,AD=3,CE=5,则AC的长为 (　　)A.9B.8C.6D.7
9. [2021平顶山期末]如图,等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点,分别过点E,F沿着平行于BA,CA方向各剪一刀,则剪下的△DEF的周长是　　　　. 
9.6　∵等边三角形纸片ABC的边长为6,E,F是边BC上的三等分点,∴EF=2.∵DE∥AB,DF∥AC,∴△DEF是等边三角形,∴剪下的△DEF的周长是2×3=6.
10. 给出下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)相等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形.其中是等边三角形的是　　　　.(填序号) 
10.①②③④　①三角形有两个角为60°,则第三个角也是60°,所以这个三角形是等边三角形,故符合题意;②根据等边三角形的判定定理,知符合题意;③三角形三个外角相等,则三个内角相等,所以这个三角形是等边三角形,故符合题意;④易证该三角形三边相等,故符合题意.
11. 教材P85习题T7变式已知:如图,在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为E,F,且DE=DF.求证:△ABC是等边三角形.
11.证明:∵D为AC的中点(已知),∴AD=CD(中点的定义).∵DE⊥AB,DF⊥BC(已知),∴∠AED=∠CFD=90°(垂直的定义).在Rt△AED和Rt△CFD中,∵AD=CD(已证),DE=DF(已知),∴Rt△AED≌Rt△CFD(H.L.),∴∠A=∠C(全等三角形的对应角相等).由(1)知,∠B=∠C,∴∠A=∠B=∠C,∴△ABC是等边三角形(三个角都相等的三角形是等边三角形).
1. 教材P84习题T3变式四张形状不同的纸片如图,用剪刀沿一条直线将它们分别剪开(只允许剪一次),不能够得到两个等腰三角形纸片的是 (　　)
1.B　对于选项A,如图1,△ACD和△BCD都是等腰三角形;对于选项B,△ABC不能够分成两个等腰三角形;对于选项C,如图2,△ACD和△BCD都是等腰三角形;对于选项D,如图3,△ACD和△BCD都是等腰三角形.
3. 已知∠ABC=30°,O是∠ABC内的一点,点O关于AB,BC的对称点分别为P,Q,则△PBQ一定是 (　　)A.等边三角形B.钝角三角形C.直角三角形D.等腰直角三角形
3.A　根据题意画出图形如图所示(其中E为OP与AB的交点,F为OQ与BC的交点).∵点O关于AB,BC的对称点分别为P,Q,∴AB⊥OP,PE=OE,BC⊥OQ,OF=FQ,易得∠OBF=∠QBF,∠OBE=∠PBE,PB=BO=BQ.∵∠ABC=30°,∴∠OBF+∠OBE=30°,∴∠PBQ=60°.又∵PB=BQ,∴△PBQ为等边三角形.
4. [2022哈尔滨萧红中学期中]在△ABC中,∠A=80°,当∠B的度数为　　　　时,△ABC是等腰三角形. 
4.50°或20°或80°
5. 如图,一个六边形的六个内角都是120°,连续四条边的长依次为1,3,3,2,则这个六边形的周长是　　　　. 
5.15　如图,分别作AB,CD,EF的延长线和反向延长线使它们交于点G,H,I.因为六边形ABCDEF的六个角都是120°,所以六边形ABCDEF的每一个外角的度数都是60°,所以△AFI,△BGC,△DHE,△GHI都是等边三角形,所以AI=AF=3,BG=BC=1,所以GI=GH=AI+AB+BG=3+3+1=7,DE=HE=HI-EF-FI=7-2-3=2,CD=HG-CG-HD=7-1-2=4,所以六边形的周长为3+1+4+2+2+3=15.
6. 教材P84习题T4变式[2020哈尔滨中考]已知:在△ABC中,AB=AC,点D、点E在边BC上,BD=CE,连接AD,AE.(1)如图1,求证:AD=AE.(2)如图2,当∠DAE=∠C=45°时,过点B作BF∥AC交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中的四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.
6.(1)证明:∵AB=AC,∴∠B=∠C.在△ABD和△ACE中,∵AB=AC,∠B=∠C,BD=CE,∴△ABD≌△ACE(),∴AD=AE.(2)解:∵AD=AE,∴∠ADE=∠AED.∵BF∥AC,∴∠FBD=∠C=45°.∵∠ABC=∠C=∠DAE=45°,∠BDF=∠ADE,∴∠F=∠BDF,∠BEA=∠BAE,∠CDA=∠CAD,∴满足条件的等腰三角形有△ABE,△ACD,△DAE,△DBF.
素养提升7. 如图1,若△ABC和△ADE均为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形.(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等,请证明;若不相等,请说明理由.(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是,请证明;若不是,请说明理由.
7.解:(1)CD=BE.证明如下:∵△ABC和△ADE均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠EAD=60°.∵∠BAE=∠BAC-∠EAC=60°-∠EAC,∠DAC=∠DAE-∠EAC=60°-∠EAC,∴∠BAE=∠DAC.在△ABE和△ACD中,∵AB=AC,∠BAE=∠CAD,AE=AD,∴△ABE≌△ACD(),∴CD=BE.
(2)△AMN是等边三角形.证明如下:∵△ABC和△ADE均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠EAD=60°.在△ABE和△ACD中,∵AB=AC,∠BAE=∠CAD,AE=AD,∴△ABE≌△ACD(),∴∠ABE=∠ACD,BE=CD.∵M,N分别是BE,CD的中点,BE=CD,∴BM=CN.在△ABM和△ACN中,∵BM=CN,∠ABM=∠ACN,AB=AC,∴△ABM≌△ACN(),∴AM=AN,∠MAB=∠NAC.∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°,∴△AMN是等边三角形.
一题练透 等边三角形的性质与判定的综合运用
如图,在等边三角形ABC的边AC的延长线上取一点E,以CE为边作等边三角形CDE,使B,D在AE的同侧,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC.[问题1]求证:△ACD≌△BCE.[问题2]求∠AOB的度数.[问题3]写出图中其他的全等三角形,并选一个说明理由.[问题4]猜想PQ和AE的位置关系,并说明理由.[问题5]求证:OC平分∠AOE.
[问题1]证明:∵△ABC和△DCE都是等边三角形,∴BC=AC,DE=DC,∠DEC=∠BCA=∠DCE=60°,∴∠ACD=∠BCE.在△ACD和△BCE中,∵AC=BC,∠ACD=∠BCE,DC=EC,∴△ACD≌△BCE().
[问题2]解:∵△ACD≌△BCE,∴∠DAC=∠CBE.∵∠ACB=∠DCE=60°,∴∠BCD=60°.∵△DCE是等边三角形,∴∠EDC=60°=∠BCD,∴BC∥DE,∴∠CBE=∠DEO,∴∠DAC=∠DEO,∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.
[问题3]解:△ACP≌△BCQ,△CQE≌△CPD.选择证明△ACP≌△BCQ,过程如下:∵△ACD≌△BCE,∴∠CAD=∠CBE,∵∠ACB=∠ECD=60°,∴∠BCQ=180°-60°×2=60°,∴∠ACB=∠BCQ=60°.在△ACP与△BCQ中,∵∠CAP=∠CBQ,AC=BC,∠ACP=∠BCQ,∴△ACP≌△BCQ().[问题4]解:PQ∥AE.理由如下:∵△ACP≌△BCQ,∴PC=QC,又∵∠BCD=60°,∴△PCQ是等边三角形,∴∠CPQ=60°,∴∠ACB=∠CPQ,∴PQ∥AE.