




初中数学沪科版九年级上册23.2解直角三角形及其应用教课内容课件ppt
展开(1) 有角先求角 无角先求边(2) 有斜用弦, 无斜用切; 宁乘毋除, 取原避中。
仰角:水平线与在它上方的视线所成的角.俯角:水平线与在它下方的视线所成的角
例1.一艘轮船在A处观测灯塔S在船的北偏东30度,轮船向正北航行15海里后到达B处,这时灯塔S恰好在船的正东.求灯塔S与B处的距离.(精确到0.1海里)
例2.在地面上,利用测角仪CD,测得旗杆顶A的仰角为45度,已知点D到旗杆底部的距离BD=28米,测角仪高CD=1.3米.求旗杆高AB(精确到0.1米)
例3.一铁路路基的横断面是等腰梯形,路基顶部的宽为9.8米,路基高为5.8米,斜坡与地面所成的角A为60度.求路基低部的宽(精确到0.1米)
坡角:坡面与水平的夹角.通常指锐角或直角.坡度(或坡比):坡面的垂直高度h与水平宽度l的比.
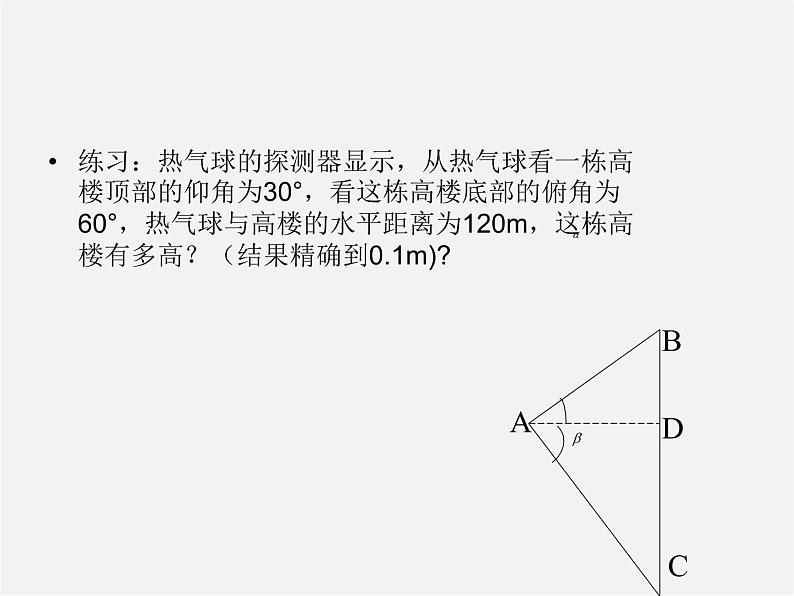
练习:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高?(结果精确到0.1m)?
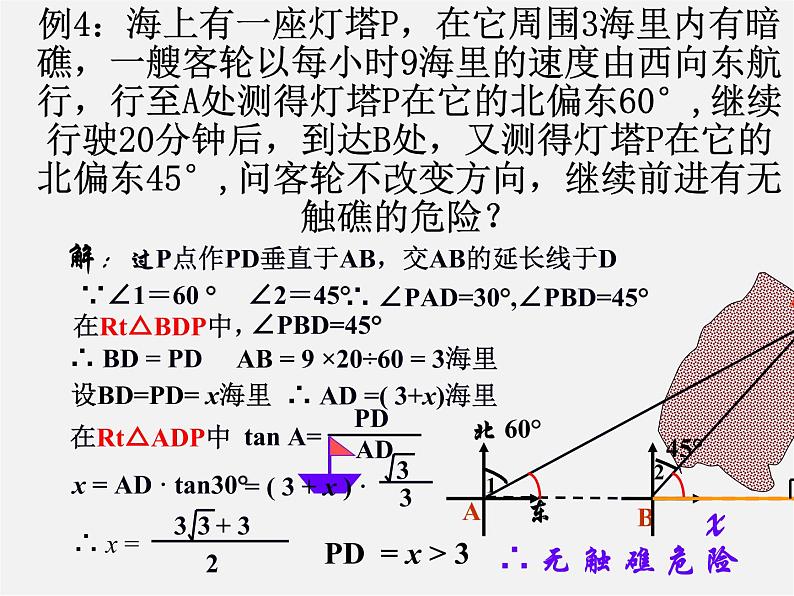
例4:海上有一座灯塔P,在它周围3海里内有暗礁,一艘客轮以每小时9海里的速度由西向东航行,行至A处测得灯塔P在它的北偏东60°,继续行驶20分钟后,到达B处,又测得灯塔P在它的北偏东45°,问客轮不改变方向,继续前进有无触礁的危险?
解:过P点作PD垂直于AB,交AB的延长线于D
∴ ∠PAD=30°,∠PBD=45°
AB = 9 ×20÷60 = 3海里
设BD=PD= x海里
∴ AD =( 3+x)海里
x = AD · tan30°
PD = x > 3
∴ 无 触 礁 危 险
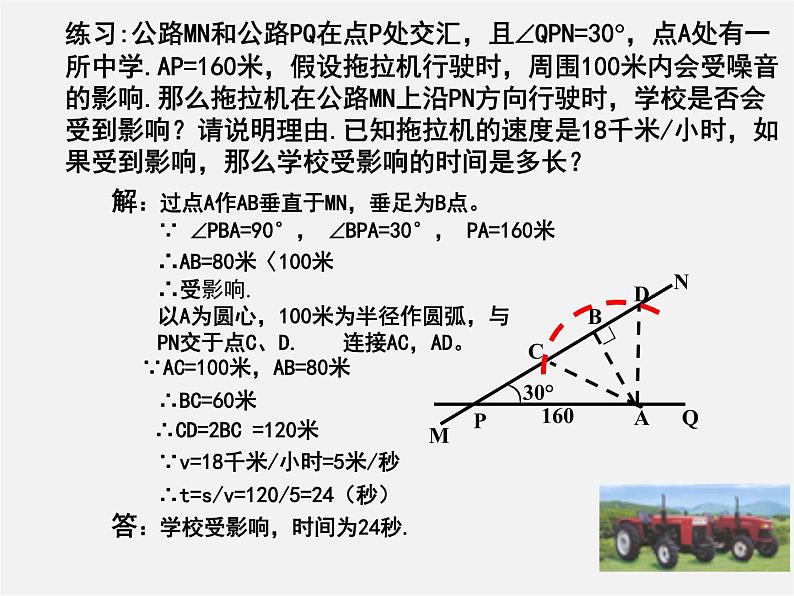
练习:公路MN和公路PQ在点P处交汇,且QPN=30,点A处有一所中学.AP=160米,假设拖拉机行驶时,周围100米内会受噪音的影响.那么拖拉机在公路MN上沿PN方向行驶时,学校是否会受到影响?请说明理由.已知拖拉机的速度是18千米/小时,如果受到影响,那么学校受影响的时间是多长?
解:过点A作AB垂直于MN,垂足为B点。
∵ PBA=90°, BPA=30°, PA=160米
∴AB=80米〈100米
以A为圆心,100米为半径作圆弧,与PN交于点C、D.
∵AC=100米,AB=80米
∴CD=2BC =120米
∵v=18千米/小时=5米/秒
∴t=s/v=120/5=24(秒)
答:学校受影响,时间为24秒.
例5 :一船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西300,又航行了半小时到达D处,望见灯塔C在西北方向,若航速为每小时20海里,求AD两点的距离,(结果不取近似值)
解:过点B作BF垂直于AC,垂足为F点。
∵BFA=90°, A=30°,AB=50米
∵ BFC=90°, CBF=45°
答:外国侦察机由B到C的速度约是207米/秒。
设外国侦察机由B到C的速度是V米/秒
解直角三角形在几何中的应用,关键是通过作垂线的方法,合理地构造出将已知元素和未知元素包含在内的直角三角形,分析已知量与未知量在这个三角形中的联系。
练习: 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200米,从飞机上看低平面控制点B的俯角α=16031/,求飞机A到控制点B的距离.
练习 某人在A处测得大厦的仰角∠BAC为300 ,沿AC方向行20米至D处,测得仰角∠BDC 为450,求此大厦的高度BC.
一 选择题 1 在下列直角三角形中,不能求出解的水( ) A 已知一直角边和所对的角 B 已知两个锐角 C 已知斜边和一个锐角 D 已知两直角边(目标1) 2 在Rt△ABC中,∠C=900,csB=2/3,则 a:b:c=( ) A 2:√5:3 B 1:√2:√3 C 2:√5:√3 D 1:2:3 3 在Rt△ ABC中,CD为斜边AB上的高,则下列线段的比等于sinA的是( ) A AB/BC B CD/AC C BD/DC D BC/AC 4 在△ ABC中,C =900,A=600,两直角边的和为14,则a=( ) A 21-7√3 B 7√3-7 C 14√3 D 1+√3(目标2) 5 在△ ABC中,∠B=450,∠C=600,BC边上的高AD=3,则BC=( ) A 3+3√3 B 2+√3 C 3+√3 D √2+√6 6 在等腰△ ABC中,顶角为锐角,一腰上的高线为1 ,这条高线与 另一腰的夹角为450,则三角形ABC的面积为() A√2/2 B √3 C 1/2 D 1/4
二 填空题(目标1) 1 在在Rt△ABC中, ∠C=900,如果已知b和∠A,则a= c= (用锐角三角函数表示)(目标2) 2在△ ABC中,C =900,A=600,a+b=3+√3,则c= 3 山坡与地面成300的倾斜角,某人上坡走60米,则他(目标3) 上升 米,坡度是 4 如图已知堤坝的横断面为梯形,AD坡面的水平宽度为 3√3米,DC=4米,B=600,则 (1)斜坡AD 的铅直高度是 (2)斜坡AD 的长是 (3)坡角A的度数是 (4)堤坝底AB的长是 (5)斜坡BC的长是
(目标3) 6 如图从山 顶A望地面的C、D 两点,俯角分别时450、600, 测得 CD=100米,设山高AB=x则列出关于X的方程是 解得x= 三 解答题(目标2) 1在在Rt△ABC中, ∠C=900,a+b=12, tgB=2,求C的值及∠ABD的度数(目标3) 2 山顶上有一座电视塔,在塔顶B处测得地面上 一点A的俯角=600,在塔底C处测得A的俯角 α=450,已知塔高为β=60米,求山高(目标3)3 我军某部在一次野外训练中,有一辆坦克准备通过一座小山,已知 山脚和山顶的水平距离为1550米,山高为565米,如果这辆坦克能够爬250的斜坡,试问:它能部能通过这座小山 ?
沪科版九年级上册23.2解直角三角形及其应用教学演示课件ppt: 这是一份沪科版九年级上册23.2解直角三角形及其应用教学演示课件ppt,共8页。PPT课件主要包含了正南或,正北方向等内容,欢迎下载使用。
初中数学23.2解直角三角形及其应用课文配套ppt课件: 这是一份初中数学23.2解直角三角形及其应用课文配套ppt课件,共15页。PPT课件主要包含了a2+b2=c2,∠A+∠B=90°等内容,欢迎下载使用。
沪科版九年级上册23.2解直角三角形及其应用教学演示课件ppt: 这是一份沪科版九年级上册23.2解直角三角形及其应用教学演示课件ppt,共17页。













