沪科版九年级上册22.3 相似三角形的性质说课ppt课件

这是一份沪科版九年级上册22.3 相似三角形的性质说课ppt课件，共13页。PPT课件主要包含了回顾与思考，议一议，相似三角形的性质，例题解析，巩固练习，作业作业本等内容，欢迎下载使用。

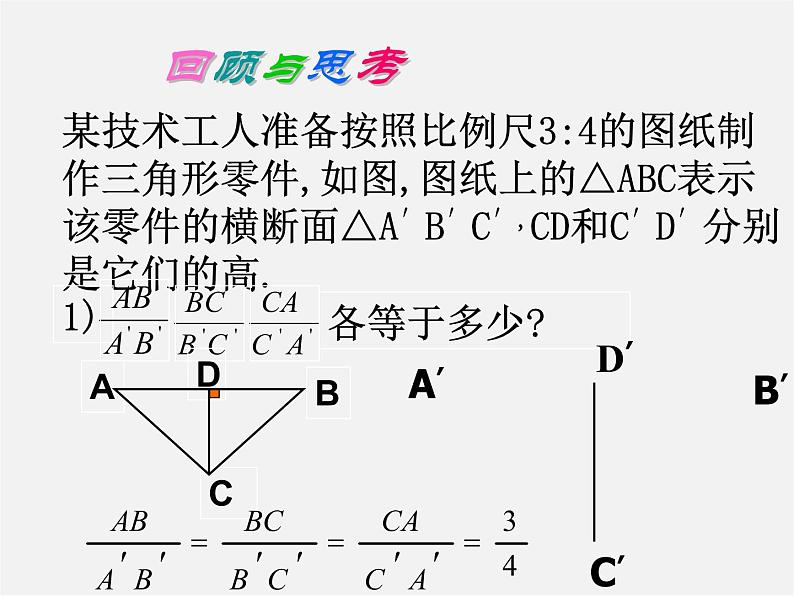
某技术工人准备按照比例尺3:4的图纸制作三角形零件,如图,图纸上的△ABC表示该零件的横断面△A′B′C′,CD和C′D′分别是它们的高.
2)△ABC与△A′B′C′相似吗?如果相似请说明理由,并指出它们的相似比.
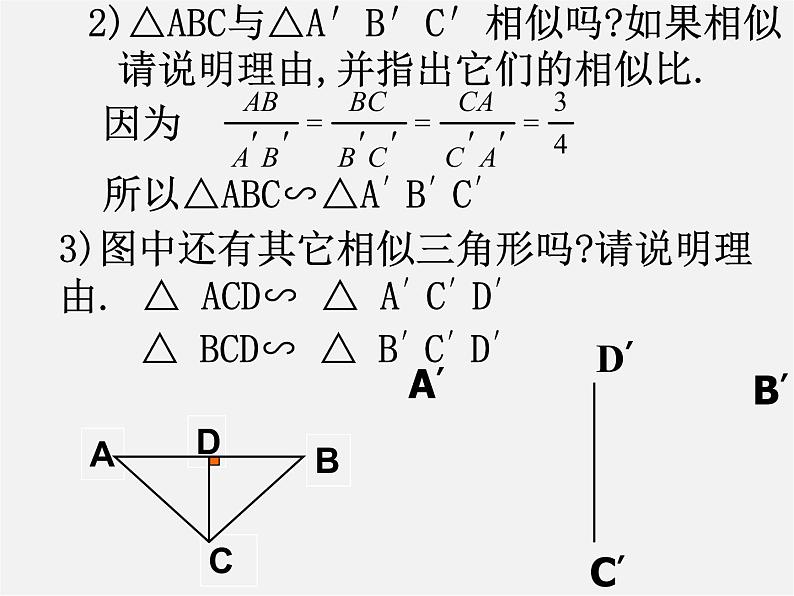
所以△ABC∽△A′B′C′
△ ACD∽ △ A′C′D′
△ BCD∽ △ B′C′D′
3)图中还有其它相似三角形吗?请说明理由.
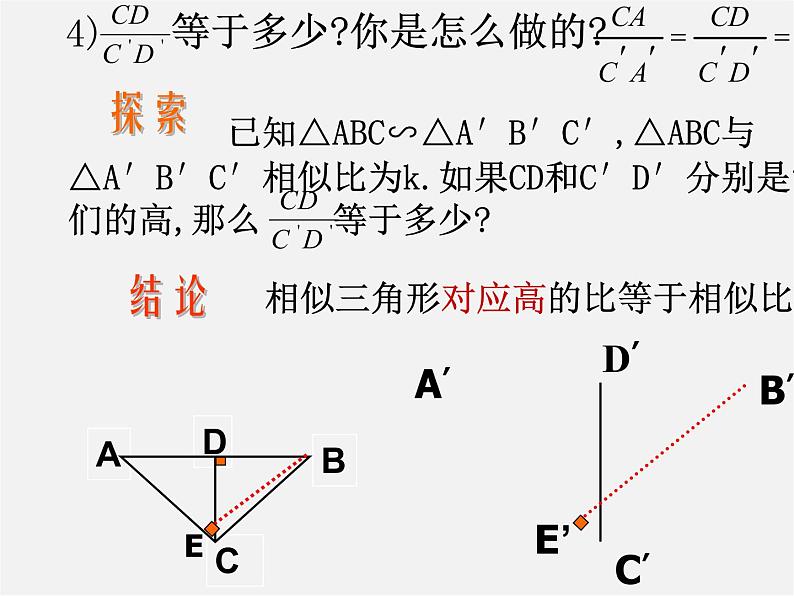
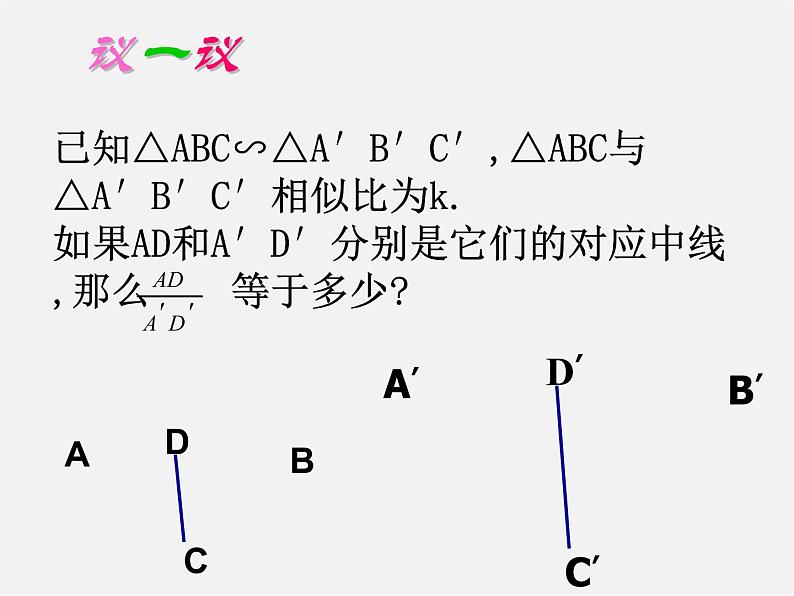
等于多少?你是怎么做的?
相似三角形对应高的比等于相似比.
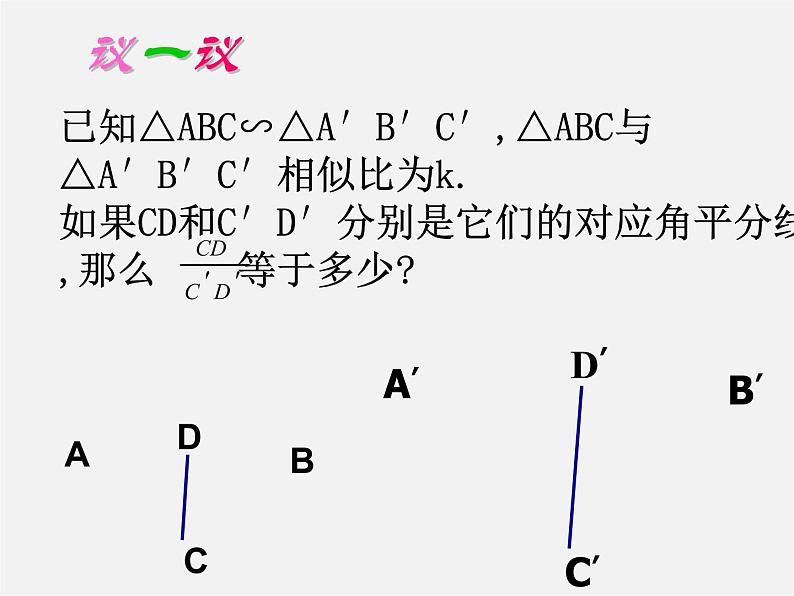
已知△ABC∽△A′B′C′,△ABC与△A′B′C′相似比为k.如果CD和C′D′分别是它们的对应角平分线,那么 等于多少?
定理1：相似三角形对应高的比，对应中线的比，对应角平分线的比都等于相似比。
1．如果两个相似三角形的对应高的比为2:3，那么对应角平分线的比是_____，对应边上的中线的比是______ 。2．△ABC与△A'B'C'的相似比为3:4，若BC边上的高AD＝12cm，则B'C'边上的高A'D'＝_____ 。
4．如图，△ABC∽△A’B′C′，对应中线AD＝6cm，A’D’＝10cm，若BC＝12cm，则B’C′＝______ 。
3、已知△ABC∽△A’B′C′，如果AD和A′D′分别是它们的对应角平分线， AD＝8cm，A’D’＝3cm，则△ABC与△A′B′C′对应高的比
如图所示,在等腰△ABC中,底边BC=60cm,高 AD=40cm,四边形PQRS是正方形.(1)△ASR与△ABC相似吗?为什么?(2)求正方形PQRS的边长.解:(1) △ASR∽△ABC.理由是:
(2)由(1)可知, △ASR∽△ABC.
四边形PQRS是正方形
∠ASR= ∠B∠ARS= ∠C
设正方形PQRS的边长为x cm, 则AE=(40-x)cm,
解得,x=24.所以正方形PQRS的边长为24cm.
(相似三角形对应高的比等于相似比)
如图所示,在矩形DEFG内接于△ABC,点D、E在BC上，点F，G分别在AC，AB上，且DE=2EF，BC=21mm， △ABC的高AH=14mm，求矩形DEFG的面积。
(特别注意“对应”二字)