初中数学湘教版七年级下册5.2 旋转课前预习课件ppt

这是一份初中数学湘教版七年级下册5.2 旋转课前预习课件ppt，共28页。PPT课件主要包含了旋转中心，旋转角，旋转的基本性质，4连接DE，作法二等内容，欢迎下载使用。

1.经历对生活中有关图形的旋转现象进行观察、分析以及动手操作、画图等过程，掌握有关画图的操作技能，发展初步的审美能力，增强对图形欣赏的意识.
2.通过具体实例认识旋转，理解旋转前后两个图形对应点到旋转中心的距离相等、对应点与旋转中心的连线所成的角彼此相等的性质.
将一个平面图形上的每一个点绕这个平面内一定点沿某个方向旋转同一个角度，这样的图形变换称为 ，这个定点称为 ，转动的角称为 .
旋转不改变图形的形状和大小.
【例1】如图所示，如果把钟表的指针看成四边形AOBC，它绕O点按顺时针方向旋转得到四边形DOEF．在这个旋转过程中：
１.旋转中心是什么？旋转角 是什么？２.经过旋转，点A，B分别移 动到什么位置？３.线段OA与OD的长有什么关系？ 线段OB与OE呢？４.∠AOD与∠BOE有什么大小 关系？
解析：1.旋转中心是O点，旋转角是∠AOD.旋转角还可以是∠BOE.
2.点A旋转到点D的位置，点B旋转到点E的位置.
3.钟表的指针长短、形状没有变化，所以线段OA与OD是相等的.同样，线段OB与OE也是相等的.
4.因为四边形AOBC绕O点旋转到四边形DOEF的位置，在旋转的过程中，图形上的每个点同时都按相同的方向旋转相同的角度，所以∠AOD与∠BOE是相等的.
经过旋转，图形上的每一点都绕旋转中心沿相同方向转动了相同的角度.任意一对对应点与旋转中心的连线所成的角都是旋转角，旋转角彼此相等.对应点到旋转中心的距离相等.
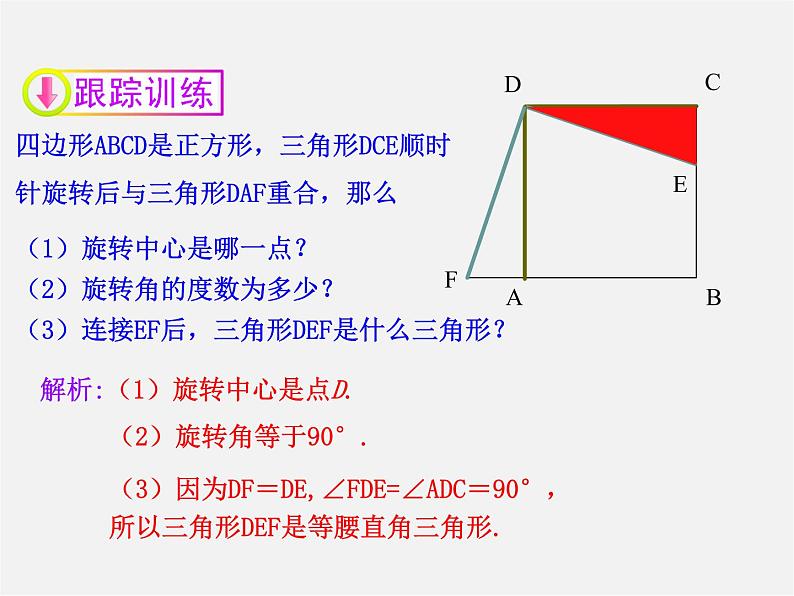
四边形ABCD是正方形，三角形DCE顺时针旋转后与三角形DAF重合，那么
（1）旋转中心是哪一点？
（2）旋转角的度数为多少？
（3）连接EF后，三角形DEF是什么三角形？
解析:（1）旋转中心是点D.
（2）旋转角等于90°.
（3）因为DF＝DE,∠FDE=∠ADC＝90°， 所以三角形DEF是等腰直角三角形.
【例2】钟表的分针匀速旋转一周需要60分．（１）指出它的旋转中心.（２）经过20分，分针旋转了多少度？解析：（１）它的旋转中心是钟表的轴心. （２）分针匀速旋转一周需要60分，因此旋转20分，分针旋转的角度为 .
1.将一个四边形进行旋转可得到右下图(1)这个四边形旋转了几次?(2)每次旋转了多少度?
解析：（1）旋转了5次.
（2）每次旋转的角度为60°.
2.在图中，正方形ABCD与正方形EFGH边长相等，这个图案可以看成是哪个“基本图案”通过旋转得到的？
【解析】（法1）整个图形可以看成是图形的八分之一(一组大小不等的三个“角”)绕中心位置，按照同一方向连续旋转45°,90°,135°,180°,225°,270°,315°，前后的图形共同组成的.
（法2）整个图形也可以看成是图形的四分之一(两组相邻的“角”)绕中心位置连续旋转90°，180°，270°，前后的图形共同组成的.
（法3）整个图形还可以看成是图形的二分之一(四组相邻的“角”)绕中心位置旋转180°，前后的图形共同组成的.
【例3】你能作出 “将方格中的小旗子绕 O点按顺时针方向旋转90˚”后的图案吗？
解析：在原图上找了四个点即O点、A点、B点、C点，四个点是表示这面小旗子的关键点.因为旋转前后两个图形的对应点到旋转中心的距离相等，对应点与旋转中心的连线所组成的旋转角彼此相等，所以根据已知：要把这面小旗绕O点按顺时针旋转90°.在方格中找到点A，B，C的对应点A1，B1，C1，然后连接，就得到了所求作的图形.
【例4】如图,三角形ABC绕C点旋转后,顶点A的对应点为点D.试确定顶点B的对应位置,以及旋转后的三角形.
1.明确旋转中心、旋转的方向与大小.
2.假设顶点B的对应点为E,则∠BCE 、 ∠ACD 都是旋转角， 且 ∠BCE =∠ACD 、CE=CB 、CD=CA.
解析：作法一（1）连接CD,
（2）以CB 为一边作∠BCF,使 得∠BCF=∠ACD.
（3）在射线CF上截取CE=CB.
则顶点B的对应位置为E点.三角形DEC就是三角形ABC绕C点旋转后的图形.
（1）以点C为圆心、CB长为半径画弧.
（2）以点D为圆心、AB长为半径画弧.
（3）两弧的交点E 即为点B的 对应点 .
（4）连接 CE，ED，DC.
在旋转过程中,确定一个三角形旋转后的位置，除需要原来的位置外，还需要什么条件？
(1)旋转中心. (2)旋转角.
在下图中，将大写字母 N 绕它右下侧的顶点按顺时针方向旋转 90°，作出旋转后的图案.
1. 如图,在等腰直角三角形ABC中∠B＝90°，将三角形ABC绕顶点A逆时针方向旋转60°后得到三角形A B′C′，则∠BAC′等于( )
A.60° 　　　 B.105°C.120° 　 　 D.135°
【解析】选B.将三角形ABC绕顶点A逆时针方向旋转60°，则∠CAC′=60°，因为三角形ABC是等腰直角三角形,所以∠BAC=45°, 所以∠BAC′= ∠CAC′+ ∠BAC=105°.
2.（天津·中考）如图，已知正方形ABCD的边长是3，E为CD边上一点，DE=1，以点A为中心，把三角形ADE顺时针旋转90°得三角形ABE′，连接EE′，则EE′的长等于 .
【解析】三角形ADE顺时针旋转90°得三角形ABE′, 所以AE＝AE′,因为∠BAD=∠EAE′＝90°，所以三角形EAE′是等腰直角三角形.因为AE2=AD2+DE2=10，所以 , EE′=　　
3.（上海·中考）已知正方形ABCD中，点E在边DC上，DE=2，EC=1（如图所示）.把线段AE绕点A旋转，使点E落在直线BC上的点F处，则F，C两点的距离为_____.
【解析】题目里只说“旋转”，并没有说顺时针还是逆时针，而且说的是“直线BC上的点”，所以有两种情况.如图所示：顺时针旋转得到F1C=1，逆时针旋转得到F2，则F2B=DE=2，F2C=F2B+BC=5.答案：1或5
【规律方法】利用旋转解决问题紧紧抓住旋转的性质，经过旋转，利用旋转角彼此相等，对应点到旋转中心的距离相等，是用来证明角、线段相等的常用方法.
1.旋转中心在旋转过程中保持不动.2.图形中每一点都绕着旋转中心旋转了同样大小的角度，对应点到旋转中心的距离相等，对应线段、角均相等.3.旋转一定角度后能与自身重合.4.旋转作图要找准原图形的位置、旋转中心、旋转角.