初中数学浙教版八年级上册1.5 三角形全等的判定图文ppt课件

这是一份初中数学浙教版八年级上册1.5 三角形全等的判定图文ppt课件，共24页。PPT课件主要包含了等边三角形的判定，判一判并说明理由，变一变，练一练，试一试，提高题等内容，欢迎下载使用。

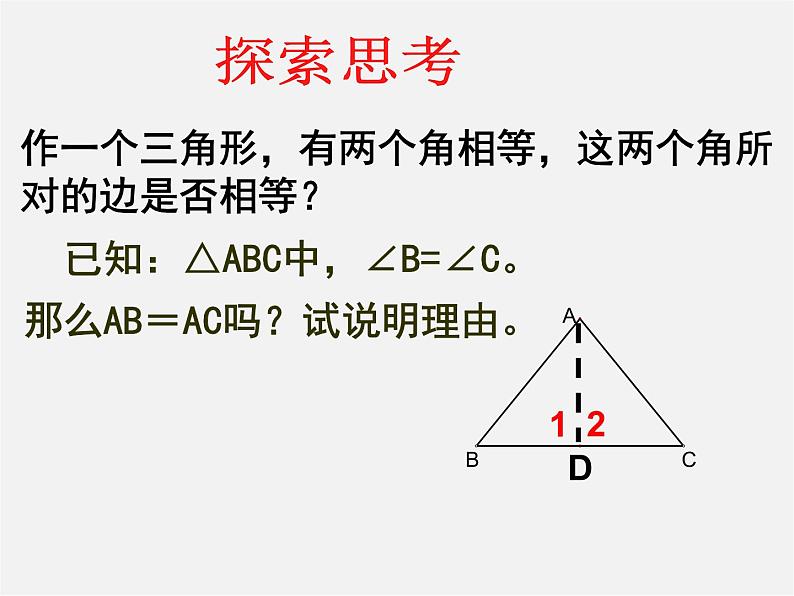
作一个三角形，有两个角相等，这两个角所对的边是否相等？
已知：△ABC中，∠B=∠C。那么AB＝AC吗？试说明理由。
2、如果一个三角形有两个角相等，那么这个三角形是等腰三角形。
即：在同一个三角形中，等角对等边。
在△ABC中， ∵ ∠B=∠C （ ）∴ AC=AB( ）
在一个三角形中，等角对等边
1、定义；有两边相等的三角形叫做等腰三角形
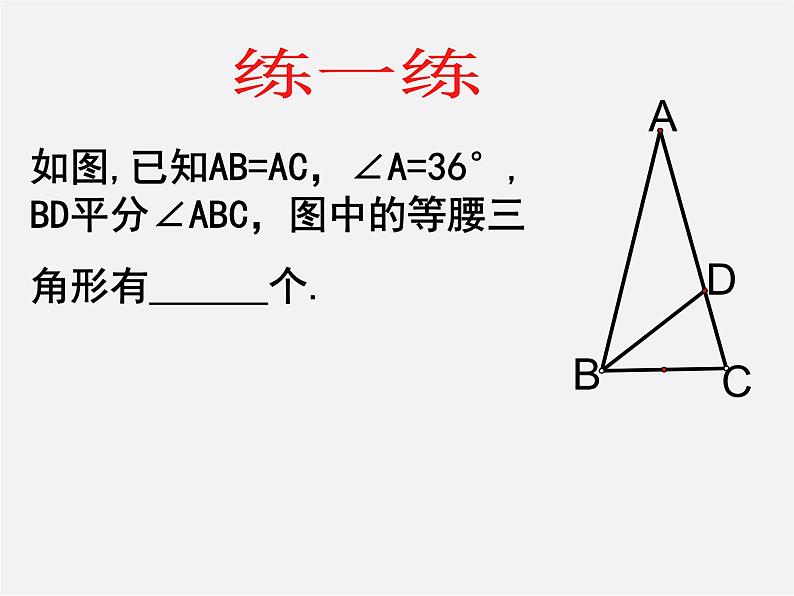
如图,已知AB=AC，∠A=36°, BD平分∠ABC，图中的等腰三角形有 个.
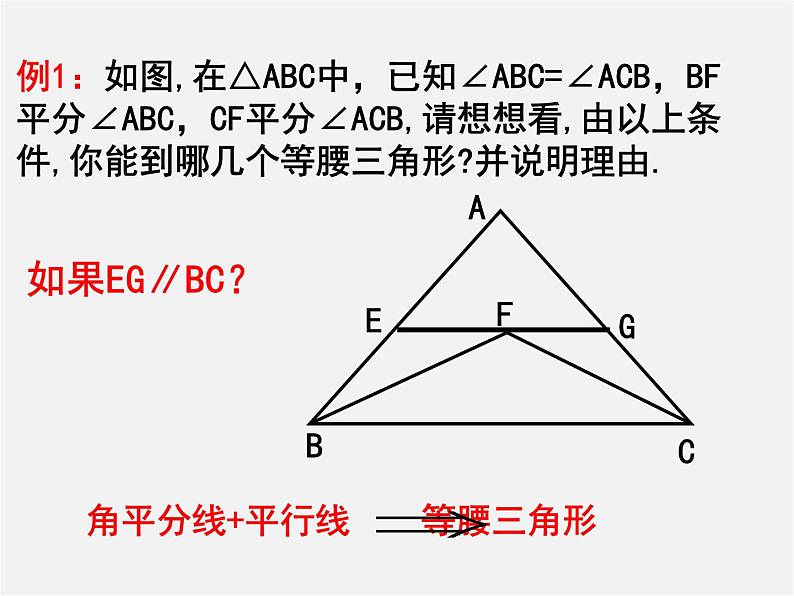
例1：如图,在△ABC中，已知∠ABC=∠ACB，BF平分∠ABC，CF平分∠ACB,请想想看,由以上条件,你能到哪几个等腰三角形?并说明理由.
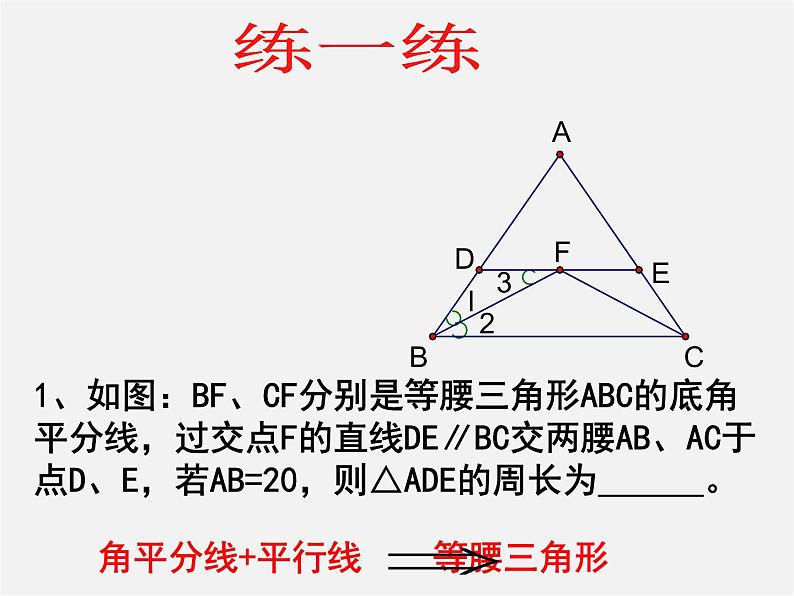
1、如图：BF、CF分别是等腰三角形ABC的底角平分线，过交点F的直线DE∥BC交两腰AB、AC于点D、E，若AB=20，则△ADE的周长为 。
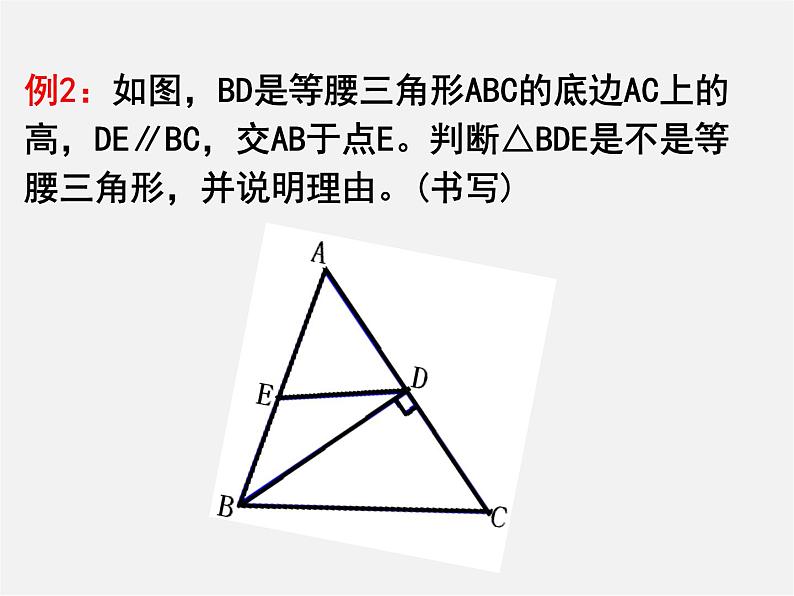
例2：如图，BD是等腰三角形ABC的底边AC上的高，DE∥BC，交AB于点E。判断△BDE是不是等腰三角形，并说明理由。(书写)
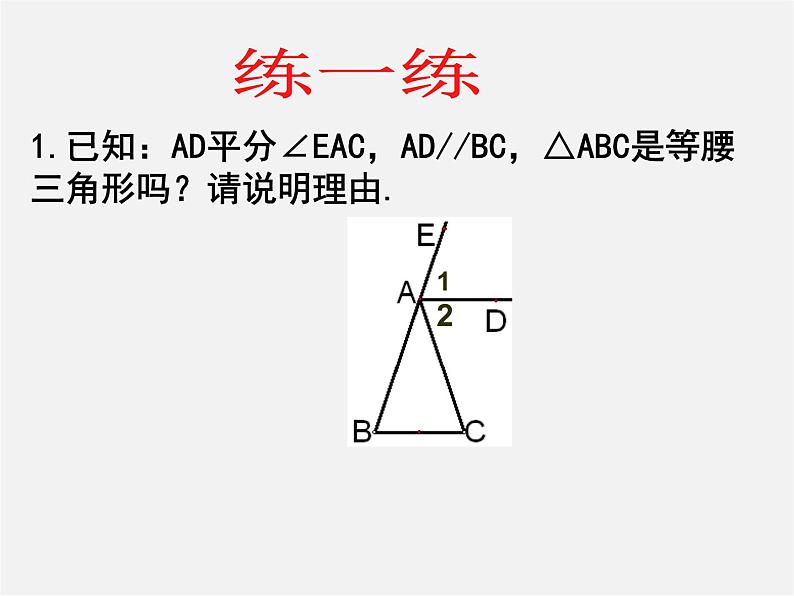
1.已知：AD平分∠EAC，AD//BC，△ABC是等腰三角形吗？请说明理由.
三条边都相等的三角形叫做等边三角形
等边三角形是特殊的等腰三角形。
三个内角都相等的三角形
有一个内角等于60 °的等腰三角形
１.在△ABC 中，AB=BC=6, ∠C=600,则CA=______
４.若三角形中最大角是600,那么这个三角形 是____ .
三条角平分线所在的直线
５.等边三角形两条高线所夹的锐角的度数是
1、三个角都是600的三角形是等边三角形.( )
5、一个角是600的等腰三角形是等边三角形.( )
4、一个底角是600的等腰三角形是等边三角形.( )
3、一个顶角是600的等腰三角形是等边三角形.( )
2、两个角都是600的三角形是等边三角形.( )
已知△ABC是等边三角形,D,E,F分别是各边上的一点,且AD=BE=CF.试说明△ DEF是等边三角形.
DE⊥BC,EF⊥AC,FD⊥AB
如图, △ABC为等边三角形, ∠ 1= ∠ 2= ∠ 3(1)求∠BEC的度数.(2) △DEF为等边三角形吗?为什么?
有两边相等的三角形是等腰三角形。
2.在同一个三角形中，等边对等角,
4.等腰三角形三线合一
2.在同一个三角形中，等角对等边。
1.两腰相等.
1.等边三角形的定义.
3.等边三角形的判定.（边、角、边+角）
4.数学思想：类比思想.
2.等边三角形的性质（边、角、三线、对称性）
5.对几何图形两方面的理解—静、动
2、已知正方形ABCD和等边三角形EAD,试求∠BEC的度数。
提高题:如图，已知AB=AC，CE=BD，则FE=FD.说明理由.
如图△ABC与△DCE都是正三角形，且B、C、E共线，连接BD、AE分别交AC、DC于F、G。(1)求证△FCG是等边三角形
(2) BD、AE交于点H，求证CH平分∠BHE
1. 已知，如图所示，在△ABC中，∠B=2∠C，AD是△ABC的角平分线，求证：AC=AB+BD。
分析：遇到关于线段的等式，需要将所有线段转化到一条线段上。
法一：在最长的线段上截取短的线段的长
法二：在短的线段上延长至长线段等长
证明：法一：在线段AC上截取点E，使AE=AB，连结DE。∵AD平分∠BAC ∴∠BAD=∠DAE 在△ABD和△AED中∴△ABD≌△AED ∴BD=DE，∠B=∠AED ∵∠B=2∠C ∴∠AED=2∠C ∵∠AED=∠C+∠EDC ∴∠C=∠EDC∴ED=EC∴BD=EC∵AC=AE+EC ∴AC=AB+BD；
法二：延长线段AB至点F，使AF=AC，连结DF。∵AD平分∠BAC∴∠FAD=∠CAD 又∵AC=AF AD=AD∴△AFD≌△ACD ∴∠F=∠C ∵∠ABC=2∠C∴∠ABC=2∠F 又∵∠ABC=∠F+∠BDF∴∠F=∠BDF ∴BF=BD ∵AF=AB+BF ∴AF=AB+BD∴AC=AB+BD。
变式：如图所示，已知AD是∠BAC的平分线，AC=AB+BD，求证：∠B=2∠C.