

2020-2021学年湖北省武汉市东西湖区七年级(上)期末数学试卷
展开1.(3分)武汉地区冬季某日最高气温5℃,最低﹣4℃,则最高气温比最低气温高( )
A.9℃B.1℃C.﹣1℃D.20℃
2.(3分)中国的领水面积约为370000km2,将数370000用科学记数法表示为( )
A.37×104B.3.7×104C.0.37×106D.3.7×105
3.(3分)将式子(﹣20)+(+3)﹣(﹣5)﹣(+7)省略括号和加号后变形正确的是( )
A.20﹣3+5﹣7B.﹣20﹣3+5+7C.﹣20+3+5﹣7D.﹣20﹣3+5﹣7
4.(3分)下列各组中的项为同类项的是( )
A.3x2y和﹣3xy2 B.﹣0.2a2b和﹣0.2x2bC.3abc 和ab D.﹣x和πx
5.(3分)如图是一个正方体的表面展开图,则原正方体中与“的”字所在的面相对的面上标的汉字是( )
A.祖B.国C.厉D.害
6.(3分)下列等式变形正确的是( )
A.如果s=ab,那么b= B.如果x=2y+1,那么mx=2my+1
C.如果x﹣3=y﹣3,那么x﹣y=0 D.如果mx=my,那么x=y
7.(3分)观察下列图形,依此规律,则第8个图形中三角形的个数是( )
A.18B.28C.32D.36
8.(3分)整理一批图书,由一个人做要40h完成,现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?如果设安排x人先做4h,下列四个方程中正确的是( )
A.+=1 B.+=1 C.+=1 D.+=1
9.(3分)如图,把一长方形纸片ABCD的一角沿AE折叠,点D的对应点D'落在∠BAC内部.若∠CAE=2∠BAD',且∠CAD'=15°,则∠DAE的度数为( )
A.12°B.24°C.39°D.45°
10.(3分)学校组织学生参加知识问答,问答活动共设有20道选择题,各题分值相同,每题必答,如表记录了A、B、C三名学生的得分情况,按此规则,参赛学生D的得分可能是( )
A.75B.63C.56D.44
二、耐心填一填(本题有6个小题,每小题3分,共18分)
11.(3分)﹣3的相反数是 .
12.(3分)如图,建筑工人在砌墙时,为了使砌的墙是直的,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的细线绳作参照线.这样做的依据是: .
13.(3分)已知x=1是关于x的方程3x﹣m=﹣3的解,则m的值是 .
14.(3分)已知多项式2x﹣y﹣1的值为5,则代数式1﹣x+y的值为 .
15.(3分)小明晚上放学到家时间是6点到7点之间,某天回家看到时钟的分针与时针所成用的度数是90°,此时的时间是 .
16.(3分)一般情况下不成立,但也有数可以使得它成立,例如:m=n=0.能使得成立的一对数m、n我们称为“相伴数对”,记为(m,n).若(x,3)是“相伴数对”,则x的值为 .
三、用心答一答。(本大题共72分,解答要求写出文字说明,证明过程或计算步骤)
17.(8分)计算:
(1)(﹣5)﹣(﹣8); (2)(﹣2)2×5﹣(﹣2)3÷4.
18.(8分)化简
(1)(2x﹣3y)+(5x+4y) (2)5a2﹣[a2+(5a2﹣2a)﹣2(a2﹣3a)]
19.(8分)解下列一元一次方程:
(1)2x﹣(x+10)=5x+2(x﹣1); (2)=.
20.(8分)某车间22名工人,生产一种食品盒子,每人每天平均生产盒身1200个或盒底2000个,一个盒身要配两个盒底,为了使每天的产品刚好配套,应该分配多少工人生产盒身,多少工人生产盒底?
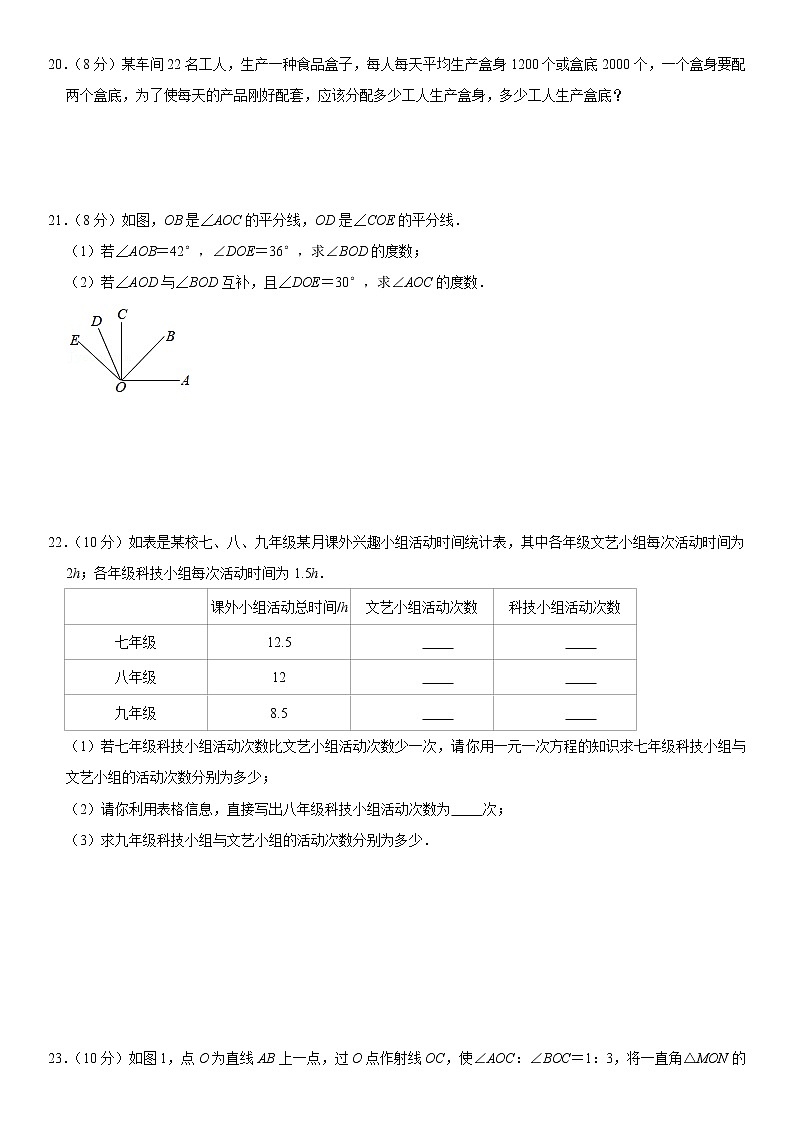
21.(8分)如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=42°,∠DOE=36°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=30°,求∠AOC的度数.
22.(10分)如表是某校七、八、九年级某月课外兴趣小组活动时间统计表,其中各年级文艺小组每次活动时间为2h;各年级科技小组每次活动时间为1.5h.
(1)若七年级科技小组活动次数比文艺小组活动次数少一次,请你用一元一次方程的知识求七年级科技小组与文艺小组的活动次数分别为多少;
(2)请你利用表格信息,直接写出八年级科技小组活动次数为 次;
(3)求九年级科技小组与文艺小组的活动次数分别为多少.
23.(10分)如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:3,将一直角△MON的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方,绕点O逆时针旋转△MON,其中旋转的角度为α(0<α<360°)
(1)将图1中的直角△MON旋转至图2的位置,使得ON落在射线OB上,此时α为 度.
(2)将图1中的直角△MON旋转至图3的位置,使得ON在∠AOC的内部,试探究∠AOM与∠NOC之间满足什么样的等量关系,并说明理由.
(3)若直角△MON绕点O按每秒5°的速度顺时针旋转,当直角△MON的直角边ON所在直线恰好平分∠AOC时,求此时直角△MON绕点O的运动时间t的值.
24.(12分)点A、B在数轴上对应的数分别为a、b,且a、b满足|a+1|+(b﹣3)2=0.
(1)如图1,求线段AB的长;
(2)若点C在数轴上对应的数为x,且x是方程2x+1=x﹣2的根,在数轴上是否存在点P使PA+PB=BC,若存在,求出点P对应的数,若不存在,说明理由;
(3)如图2,点P在B点右侧,PA的中点为M,N为PB靠近于B点的四等分点,当P在B的右侧运动时,有两个结论:①PM﹣2BN的值不变;②PM﹣BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值.
2020-2021学年湖北省武汉市东西湖区七年级(上)期末数学试卷
参考答案与试题解析
一、细心选一选(本题有10个小题,每小题3分,满分30分)
1.(3分)武汉地区冬季某日最高气温5℃,最低﹣4℃,则最高气温比最低气温高( A )
A.9℃B.1℃C.﹣1℃D.20℃
2.(3分)中国的领水面积约为370000km2,将数370000用科学记数法表示为( D )
A.37×104B.3.7×104C.0.37×106D.3.7×105
3.(3分)将式子(﹣20)+(+3)﹣(﹣5)﹣(+7)省略括号和加号后变形正确的是( C )
A.20﹣3+5﹣7B.﹣20﹣3+5+7C.﹣20+3+5﹣7D.﹣20﹣3+5﹣7
4.(3分)下列各组中的项为同类项的是( D )
A.3x2y和﹣3xy2 B.﹣0.2a2b和﹣0.2x2b C.3abc 和ab D.﹣x和πx
5.(3分)如图是一个正方体的表面展开图,则原正方体中与“的”字所在的面相对的面上标的汉字是( B )
A.祖B.国C.厉D.害
6.(3分)下列等式变形正确的是( C )
A.如果s=ab,那么b= B.如果x=2y+1,那么mx=2my+1
C.如果x﹣3=y﹣3,那么x﹣y=0 D.如果mx=my,那么x=y
7.(3分)观察下列图形,依此规律,则第8个图形中三角形的个数是( C )
A.18B.28C.32D.36
【分析】根据图示,第1个图形中三角形的个数为:4个;第2个图形中三角形的个数为:4+4=8 (个);第3个图形中三角形的个数为:4+4+4=12 (个).第n个图形中三角形的个数为:4n个,从而求得第8个图形中三角形的个数.
【解答】解:第1个图形中三角形的个数为:4×1=4个;
第2个图形中三角形的个数为:4+4=4×2=8 (个);
第3个图形中三角形的个数为:4+4+4=4×3=12 (个);
第n个图形中三角形的个数为:4n个,
当n=8时,4×8=32个,
故选:C.
【点评】此题主要考查了数字变化规律,解决此类探究性问题,关键在观察、分析已知数据.
8.(3分)整理一批图书,由一个人做要40h完成,现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人工作?如果设安排x人先做4h,下列四个方程中正确的是( B )
A.+=1 B.+=1 C.+=1 D.+=1
【分析】由一个人做要40小时完成,即一个人一小时能完成全部工作的,就是已知工作的速度.本题中存在的相等关系是:这部分人4小时的工作+增加2人后8小时的工作=全部工作.设全部工作是1,这部分共有x人,就可以列出方程.
【解答】解:设应先安排x人工作,
根据题意得:+=1
故选:B.
【点评】本题考查了由实际问题抽象出一元二次方程,是一个工作效率问题,理解一个人做要40小时完成,即一个人一小时能完成全部工作的,这一个关系是解题的关键.
9.(3分)如图,把一长方形纸片ABCD的一角沿AE折叠,点D的对应点D'落在∠BAC内部.若∠CAE=2∠BAD',且∠CAD'=15°,则∠DAE的度数为( C )
A.12°B.24°C.39°D.45°
【分析】由折叠性质得∠DAE=∠EAD′,由长方形的性质得∠DAE+∠EAD′+∠BAD′=90°,根据角的和差倍分关系得∠BAD′=12°,最后根据∠DAE=∠EAD′=∠CAE+∠CAD′可得答案.
【解答】解:∵长方形纸片ABCD的一角沿AE折叠,
∴∠DAE=∠EAD′,
∵ABCD是长方形,
∴DA⊥AB,
∴∠DAE+∠EAD′+∠BAD′=90°,即2∠EAD′+∠BAD′=90°,
∴2(∠CAE+∠CAD′)+∠BAD′=90°,
∵∠CAE=2∠BAD′,∠CAD′=15°,
∴2(2∠BAD′+15°)+∠BAD′=90°,
∴30°+5∠BAD′=90°,
∴∠BAD′=12°,
∴∠DAE=∠EAD′=∠CAE+∠CAD′
=2∠BAD′+∠CAD′
=2×12°+15°
=39°,
∴∠DAE=39°.
故选:C.
【点评】此题考查的是角的计算、折叠性质、数形结合思想,掌握折叠性质是解决此题关键.
10.(3分)学校组织学生参加知识问答,问答活动共设有20道选择题,各题分值相同,每题必答,如表记录了A、B、C三名学生的得分情况,按此规则,参赛学生D的得分可能是( D )
A.75B.63C.56D.44
【分析】根据表格中3名参赛学生的得分情况,可知答错一题倒扣2分,设参赛学生E答错x道题(0≤x≤20,且x为整数),则其得分值为:100﹣7x,然后逐个选项进行计算,结果符合x的取值范围的为正确答案.
【解答】解:根据表格数据,A学生答对20道得分100,由B、C同学得分情况可知答错一题倒扣2分,
故设参赛学生D答错x道题(0≤x≤20,且x为整数),则其得分值为:100﹣7x
选项A:令100﹣7x=75,解得x=,故本选项不符合题意;
选项B:令100﹣7x=63,解得x=,故本选项不符合题意;
选项C:令100﹣7x=56,解得x=,故本选项不符合题意;
选项D:令100﹣7x=44,解得x=8,故本选项符合题意.
故选:D.
【点评】本题为一元一次方程的实际应用,根据表格求出答错一题倒扣2分,正确列方程是解题的关键.
二、耐心填一填(本题有6个小题,每小题3分,共18分)
11.(3分)﹣3的相反数是 3 .
12.(3分)如图,建筑工人在砌墙时,为了使砌的墙是直的,经常在两个墙脚的位置分别插一根木桩,然后拉一条直的细线绳作参照线.这样做的依据是: 两点确定一条直线 .
13.(3分)已知x=1是关于x的方程3x﹣m=﹣3的解,则m的值是 6 .
14.(3分)已知多项式2x﹣y﹣1的值为5,则代数式1﹣x+y的值为 ﹣ .
15.(3分)小明晚上放学到家时间是6点到7点之间,某天回家看到时钟的分针与时针所成用的度数是90°,此时的时间是 6时分或6时分 .
【分析】可设此时的时间是6时x分,根据时钟的分针与时针所成用的度数是90°,列出方程计算即可求解.
【解答】解:设此时的时间是6时x分,依题意有
180+x﹣6x=90,
解得x=;
或6x﹣(180+x)=90,
解得x=.
故此时的时间是6时分或6时分.
故答案为:6时分或6时分.
【点评】本题考查一元一次方程的应用,钟表分针所转过的角度计算.在钟表问题中,常利用时针与分针转动的度数关系:分针每转动1°时针转动( )°,并且利用起点时间时针和分针的位置关系建立角.
16.(3分)一般情况下不成立,但也有数可以使得它成立,例如:m=n=0.能使得成立的一对数m、n我们称为“相伴数对”,记为(m,n).若(x,3)是“相伴数对”,则x的值为 ﹣ .
【分析】利用新定义“相伴数对”列出算式,计算即可求出x的值.
【解答】解:根据题意得:,
去分母,得:15x+30=6x+18,
移项,得:15x﹣6x=18﹣30,
合并同类项,得:9x=﹣12,
解得:x=﹣.
故答案为:﹣.
【点评】此题考查了等式的性质,弄清题中的新定义,能够正确解一元一次方程是解本题的关键.
三、用心答一答。(本大题共72分,解答要求写出文字说明,证明过程或计算步骤)
17.(8分)计算:
(1)(﹣5)﹣(﹣8);(2)(﹣2)2×5﹣(﹣2)3÷4.
【解答】解:(1)(﹣5)﹣(﹣8)
=﹣5+8
=3;
(2)(﹣2)2×5﹣(﹣2)3÷4
=4×5﹣(﹣8)÷4
=20+2
=22.
18.(8分)化简
(1)(2x﹣3y)+(5x+4y)(2)5a2﹣[a2+(5a2﹣2a)﹣2(a2﹣3a)]
【解答】解:(1)(2x﹣3y)+(5x+4y)=7x+y;
(2)5a2﹣[a2+(5a2﹣2a)﹣2(a2﹣3a)]=5a2﹣a2﹣5a2+2a+2a2﹣6a=a2﹣4a.
19.(8分)解下列一元一次方程:
(1)2x﹣(x+10)=5x+2(x﹣1);
(2)=.
【解答】解:(1)去括号得:2x﹣x﹣10=5x+2x﹣2,
移项得:2x﹣x﹣5x﹣2x=﹣2+10,
合并得:﹣6x=8,
解得:x=﹣;
(2)去分母,得:10(3x+2)﹣20=5(2x﹣1)﹣4(2x+1),
去括号,得:30x+20﹣20=10x﹣5﹣8x﹣4,
移项合并,得:28x=﹣9,
解得:x=﹣.
【点评】此题考查了解一元一次方程,熟练掌握解一元一次方程的步骤是解本题的关键.
20.(8分)某车间22名工人,生产一种食品盒子,每人每天平均生产盒身1200个或盒底2000个,一个盒身要配两个盒底,为了使每天的产品刚好配套,应该分配多少工人生产盒身,多少工人生产盒底?
【分析】根据“一个盒身要配两个盒底”,生产盒底的数量应是盒身的2倍,所以本题中的等量关系是:每人每天平均生产盒身的个数×生产盒身的人数×2=每人每天平均生产盒底的个数×生产盒底的人数.据此等量关系式可列方程解答.
【解答】解:设应分配x名工人生产盒身,则生产盒底的工人应是(22﹣x)名,根据题意得
1200x×2=2000×(22﹣x),
解得:x=10,
22﹣x=22﹣10=12,
答:应该分配10工人生产盒身,12名工人生产盒底.
【点评】此题考查一元一次方程的实际运用,根据一个盒身要配两个盒底,找出题目中的等量关系,再列方程解答.
21.(8分)如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)若∠AOB=42°,∠DOE=36°,求∠BOD的度数;
(2)若∠AOD与∠BOD互补,且∠DOE=30°,求∠AOC的度数.
【分析】(1)根据角平分线的性质可得∠AOB=∠BOC==42°,∠COD=∠DOE=36°,易得结果;
(2)根据互补的定义可得∠AOD+∠BOD=180°,利用角的加减运算即可.
【解答】解:(1)∵OB是∠AOC的平分线,OD是∠COE的平分线,∠AOB=42°,∠DOE=36°,
∴∠AOB=∠BOC==42°,∠COD=∠DOE=36°,
∴∠BOD=∠BOC+∠DOC=42°+36°=78°;
(2)∵∠AOD与∠BOD互补,∠BOC=,
∴∠AOD+∠BOD=180°,
∴∠AOC+∠COD+∠AOC+∠COD=180°,
∵∠DOE=30°,
∴∠COD=30°,
∴,
∴=180°,
∴∠AOC=80°.
【点评】本题主要考查了角平分线的定义,互补的性质等,根据图形运用角的加减运算是解答此题的关键.
22.(10分)如表是某校七、八、九年级某月课外兴趣小组活动时间统计表,其中各年级文艺小组每次活动时间为2h;各年级科技小组每次活动时间为1.5h.
(1)若七年级科技小组活动次数比文艺小组活动次数少一次,请你用一元一次方程的知识求七年级科技小组与文艺小组的活动次数分别为多少;
(2)请你利用表格信息,直接写出八年级科技小组活动次数为 4 次;
(3)求九年级科技小组与文艺小组的活动次数分别为多少.
【分析】(1)设七年级科技小组活动次数为x次,则文艺小组活动次数为(x+1)次,根据七年级课外小组活动总时间为12.5h,即可得出关于x的一元一次方程,解之即可得出结论;
(2)设八年级文艺小组活动次数为m次,科技小组活动次数为n次,根据八年级课外小组活动总时间为12h,即可得出关于m,n的二元一次方程,再结合m,n均为正整数即可得出结论;
(3)设九年级文艺小组活动次数为a次,科技小组活动次数为b次,根据九年级课外小组活动总时间为8.5h,即可得出关于a,b的二元一次方程,再结合a,b均为正整数即可得出结论.
【解答】解:(1)设七年级科技小组活动次数为x次,则文艺小组活动次数为(x+1)次,
依题意得:1.5x+2(x+1)=12.5,
解得:x=3,
∴x+1=4.
故答案为:4;3.
(2)设八年级文艺小组活动次数为m次,科技小组活动次数为n次,
依题意得:2m+1.5n=12,
∴n=8﹣m.
又∵m,n均为正整数,
∴.
故答案为:4.
(3)设九年级文艺小组活动次数为a次,科技小组活动次数为b次,
依题意得:2a+1.5b=8.5,
∴b=,
又∵a,b均为正整数,
∴.
故答案为:2;3.
【点评】本题考查了二元一次方程的应用以及一元一次方程的应用,解题的关键是:(1)找准等量关系,正确列出一元一次方程;(2)找准等量关系,正确列出二元一次方程;(3)找准等量关系,正确列出二元一次方程.
23.(10分)如图1,点O为直线AB上一点,过O点作射线OC,使∠AOC:∠BOC=1:3,将一直角△MON的直角顶点放在点O处,边OM在射线OB上,另一边ON在直线AB的下方,绕点O逆时针旋转△MON,其中旋转的角度为α(0<α<360°)
(1)将图1中的直角△MON旋转至图2的位置,使得ON落在射线OB上,此时α为 90 度.
(2)将图1中的直角△MON旋转至图3的位置,使得ON在∠AOC的内部,试探究∠AOM与∠NOC之间满足什么样的等量关系,并说明理由.
(3)若直角△MON绕点O按每秒5°的速度顺时针旋转,当直角△MON的直角边ON所在直线恰好平分∠AOC时,求此时直角△MON绕点O的运动时间t的值.
【分析】首先根据∠AOC:∠BOC=1:3,∠AOC+∠BOC=180°,求出∠AOC=45°和∠BOC135°;
(1)根据旋转角等于∠NOB=90°,即可求解;
(2)根据∠AOM+∠AON=90°,∠AON+∠CON=∠45°,即可求解;
(3)先求出旋转角,再除以5即可求解.
【解答】解:∵∠AOC:∠BOC=1:3,∠AOC+∠BOC=180°,
∴∠AOC=45°,∠BOC=135°
(1)由ON落在射线OB上,可知旋转角为:∠NOB=90°;
故答案为90.
(2)∵∠AOM+∠AON=90°,∠AON+∠NOC=∠AOC=45°,
∴∠AOM﹣∠NOC=45°;
(3)∵ON所在直线恰好平分∠AOC,
∴∠AON=∠AOC÷2=45°÷2=22.5°,
此时旋转角为:90°+22.5°=112.5°
112.5÷5=22.5(秒),
或(112.5+180)÷5=58.5(秒)
所以直角△MON绕点O的运动时间是22.5秒或58.5秒.
【点评】此题主要考查角的运算和旋转的基础知识,理清图形中的角的和差关系,以及旋转的意义是解题的关键.
24.(12分)点A、B在数轴上对应的数分别为a、b,且a、b满足|a+1|+(b﹣3)2=0.
(1)如图1,求线段AB的长;
(2)若点C在数轴上对应的数为x,且x是方程2x+1=x﹣2的根,在数轴上是否存在点P使PA+PB=BC,若存在,求出点P对应的数,若不存在,说明理由;
(3)如图2,点P在B点右侧,PA的中点为M,N为PB靠近于B点的四等分点,当P在B的右侧运动时,有两个结论:①PM﹣2BN的值不变;②PM﹣BN的值不变,其中只有一个结论正确,请判断正确的结论,并求出其值.
【分析】(1)利用非负数的性质求出a与b的值,即可得到线段AB的长;
(2)求出已知方程的解确定出x,得到C表示的点,设点P在数轴上对应的数是m,由PA+PB=BC确定出P位置,即可做出判断;
(3)设P点所表示的数为n,就有PA=n+1,PB=n﹣3,根据条件就可以表示出PM=(n+1),PN=(n﹣3),再分别代入①PM﹣2BN和②PM﹣BN求出其值即可.
【解答】解:(1)∵|a+1|+(b﹣3)2=0,
∴a+1=0,b﹣3=0,
∴a=﹣1,b=3,
∵点A、B在数轴上对应的数分别为a、b,
∴AB=3﹣(﹣1)=4;
(2)解方程方程2x+1=x﹣2,得x=﹣2,
即C在数轴上对应的数为﹣2.
设点P在数轴上对应的数是m,
∵PA+PB=BC,
∴|m+1|+|m﹣3|=3﹣(﹣2),
令m+1=0,m﹣3=0,
解得m=﹣1,m=3.
①当m≤﹣1时,
﹣m﹣1+3﹣m=5,
m=﹣1.5;
②当﹣1<m≤3时,
m+1+3﹣m=5,m无解;
③当m>3时,
m+1+m﹣3=5,
m=3.5.
∴点P对应的数为﹣1.5或3.5时,PA+PB=BC;
(3)设P点所表示的数为n,
∴PA=n+1,PB=n﹣3.
∵PA的中点为M,
∴PM=PA=(n+1),
∵N为PB的四等分点且靠近于B点,
∴BN=PB=(n﹣3),
∴①PM﹣2BN=(n+1)﹣2×(n﹣3)=2(不变);
②PM﹣BN=(n+1)﹣×(n﹣3)=n+1(随点P的变化而变化).
即正确的结论为①PM﹣2BN的值不变,其值为2.
【点评】本题考查了一元一次方程的运用,分类思想的运用,数轴的运用,数轴上任意两点间的距离公式的运用,去绝对值的运用,解答时灵活运用两点间的距离公式求解是关键.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2021/12/14 13:39:18;用户:刘富良;邮箱:287520833@qq.cm;学号:13137786参赛学生
答对题数
答错题数
得分
A
20
0
100
B
19
1
93
C
15
5
65
课外小组活动总时间/h
文艺小组活动次数
科技小组活动次数
七年级
12.5
八年级
12
九年级
8.5
参赛学生
答对题数
答错题数
得分
A
20
0
100
B
19
1
93
C
15
5
65
课外小组活动总时间/h
文艺小组活动次数
科技小组活动次数
七年级
12.5
4
3
八年级
12
3
4
九年级
8.5
2
3
2021-2022学年湖北省武汉市东西湖区七年级(上)期中数学试卷(含答案): 这是一份2021-2022学年湖北省武汉市东西湖区七年级(上)期中数学试卷(含答案),共14页。试卷主要包含了选一选,比比谁细心,填一填,看看谁仔细,解一解,试试谁更棒等内容,欢迎下载使用。
2022-2023学年湖北省武汉市东西湖区七年级(下)期末数学试卷(含解析): 这是一份2022-2023学年湖北省武汉市东西湖区七年级(下)期末数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
2022-2023学年湖北省武汉市东西湖区七年级(下)期末数学试卷: 这是一份2022-2023学年湖北省武汉市东西湖区七年级(下)期末数学试卷,共20页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。












