





2021学年第八章 二元一次方程组综合与测试复习ppt课件
展开这是一份2021学年第八章 二元一次方程组综合与测试复习ppt课件,共30页。PPT课件主要包含了有关概念,方程组的解法,知识应用,解得K14,依题意x+y12,解法2根据题意得,行程问题,图表问题,总量不变问题,解这个方程组得等内容,欢迎下载使用。
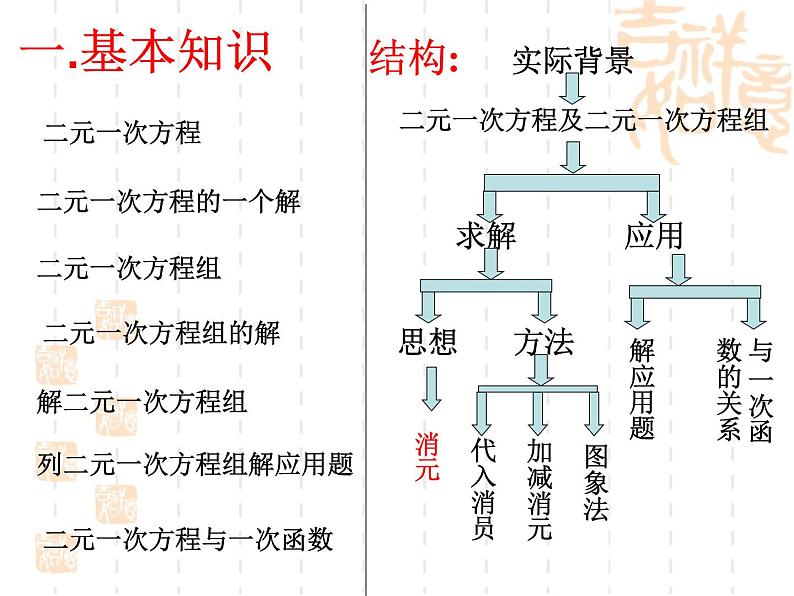
二元一次方程及二元一次方程组
列二元一次方程组解应用题
二元一次方程与一次函数
1.二元一次方程:通过化简后,只有两个未知数,并且所含未知数的项的次数都是1,系数都不是0的整式方程,叫做二元一次方程.
2.二元一次方程的解:使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
3.二元一次方程组:由两个一次方程组成,共有两个未知数的方程组,叫做二元一次方程组.
4.二元一次方程组的解:二元一次方程组中各个方程的公共解,叫做二元一次方程组的解.
根据方程未知数的系数特征确定用哪一种解法.
基本思想或思路——消元
常用方法————代入法和加减法
用代入法解二元一次方程组的步骤:
(1).求表达式:从方程组中选一个系数比较简单的方程,将此方程中的一个未知数,如y,用含x的代数式表示;
(2).把这个含x的代数式代入另一个方程中,消去y,得到一个关于x的一元一次方程;
(3).解一元一次方程,求出x的值;
(4).再把求出的x的值 代入变形后的方程,求出y的值.
用加减法解二元一次方程组的步骤:
(1).利用等式性质把一个或两个方程的两边都乘以适当的数,变换两个方程的某一个未知数的系数,使其绝对值相等;
(2).把变换系数后的两个方程的两边分别相加或相减,消去一个未知数,得一元一次方程;
(3).解这个一元一次方程,求得一个未知数的值 ;
(4).把所求的这个未知的值代入方程组中较为简便的一个方程,求出另一个未知数,从而得到方程的解 .
6.列二元一次方程解决实际问题的一般步骤: 审: 设: 列: 解: 答:
审清题目中的等量关系.
根据等量关系,列出方程组.
解方程组,求出未知数.
检验所求出未知数是否符合题意,写出答案.
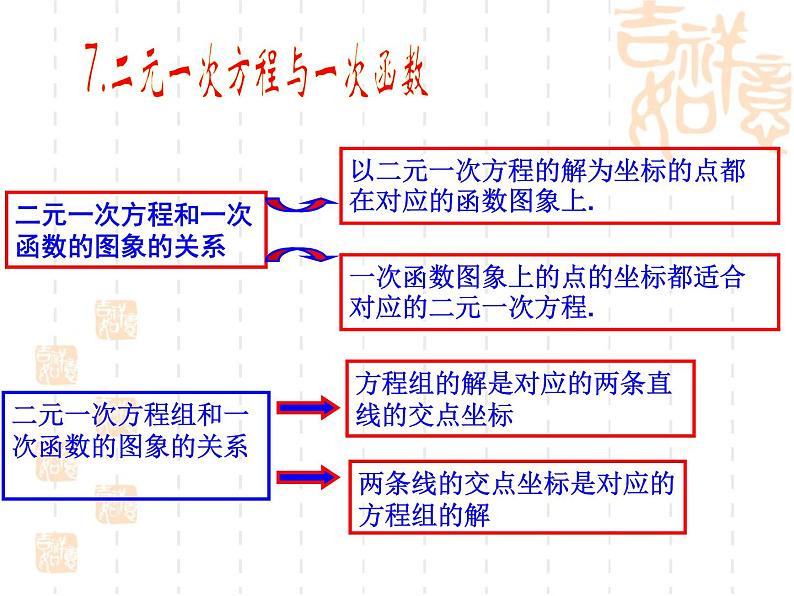
7.二元一次方程与一次函数
5.二元一次方程2m+3n=11 ( )A.任何一对有理数都是它的解.B.只有两组解.C.只有两组正整数解.D.有负整数解.
6.若点P(x-y,3x+y)与点Q(-1,-5)关于X轴对称,则x+y=______.
7.已知|2x+3y+5|+(3x+2Y-25)2=0,则x-y=______.
8.若两个多边形的边数之比是2:3,两个多边形的内角和是1980°,求这两个多边形的边数.
解法1:解这个方程组,得
所以(2k-6) +(4-k)=12
解这个方程组,得k=14
四.列二元一次方程组解应用题专题训练:
1.相遇问题:甲的路程+乙的路程=总的路程 (环形跑道):甲的路程+乙的路程=一圈长
2.追及问题:快者的路程-慢者的路程=原来相距路 程 (环形跑道): 快者的路程-慢者的路程=一圈长
3.顺逆问题:顺速=静速+水(风)速 逆速=静速-水(风)速
例1.某人要在规定的时间内由甲地赶往乙地,如果他以每小时50千米的速度行驶,就会迟到24分钟,如果他以每小时75千米的速度行驶,就会提前24分钟 到达乙地,求甲、乙两地间的距离.
解:设甲、乙两地间的距离为S千米,规定时间为t小时,根据题意得方程组
例2.甲、乙二人以不变的速度在环形路上跑步,如果同时同地出发,相向而行,每隔2分钟相遇一次;如果同向而行,每隔6分钟相遇一次.已知甲比乙跑得快,甲、乙每分钟各跑多少圈?
解:设甲、乙二人每分钟各跑x、y圈,根据题意得方程组
1.某学校现有甲种材料35㎏,乙种材料29㎏,制作A.B两种型号的工艺品,用料情况如下表:
(1)利用这些材料能制作A.B两种工艺品各多少件?(2)若每公斤甲.乙种材料分别为8元和10元,问制作A.B两种型号的工艺品各需材料多少钱?
1.入世后,国内各汽车企业展开价格大战,汽车价格大幅下降,有些型号的汽车供不应求。某汽车生产厂接受了一份订单,要在规定的日期内生产一批汽车,如果每天生产35辆,则差10辆完成任务,如果每天生产40辆,则可提前半天完成任务,问订单要多少辆汽车,规定日期是多少天?
解:设订单要辆x汽车,规定日期是y天,根据题意得方程组
答:订单要220辆汽车,规定日期是6天
4.销售问题:标价×折扣=售价售价-进价=利润利润率=
1.已知甲.乙两种商品的标价和为100元,因市场变化,甲商品打9折,乙商品提价5﹪,调价后,甲.乙两种商品的售价和比标价和提高了2﹪,求甲.乙两种商品的标价各是多少?
答:甲种商品的标价是20元,乙种商品的标价是80元.
解:设甲、乙两种商品的标价分别为x、y元,根据题意,得
例:某车间每天能生产甲种零件120个,或者乙种零件100个,或者丙种零件200个,甲,乙,丙3种零件分别取3个,2个,1个,才能配一套,要在30天内生产最多的成套产品,问甲,乙,丙3种零件各应生产多少天?
1.已知函数 的图象交于点P,则点P的坐标为( ).(A)(-7,-3) (B)(3,-7) (C)(-3,-7) (D)(-3,7)2.已知直线 与 直线相交于点,则的值分别为( ).(A) 2,3 (B) 3,2 (C) (D)
五.二元一次方程与一次函数专题训练:
4.在同一直角坐标系内分别作出一次函数 和 的图象, 观察图象并回答问题:
(1)这两个图象有交点吗?交点坐标是什么?
(2)方程组 的解是什么?
(3)交点的坐标与方程组的解有什么关系?
例1.A、B两地相距36千米.甲从A地出发步行到B地,乙从B地出发步行到A地.两人同时出发,4小时相遇,6小时后 ,甲所余路程为乙所余路程的2倍,求两人的速度.
解:设甲、乙的速度分别为x千米/小时和y千米/小时.
答:甲、乙的速度分别为4千米/小时和5千米/小时.
2. 下表是某一周甲、乙两种股票的收盘价(股票每天交易结束时的价格)
张师傅在该周内持有若干甲、乙两种股票,若按照两种股票每天收盘价计算(不计手续费、税费行等),该人账户中星期二比星期一多获利200元,星期三比星期二多获利1300元,试问张师傅持有甲、乙股票各多少股?
解:设张师傅持有甲种股票x股,乙种股票y股,根据题意,得
答:张师傅持有甲种股票1000股,乙种股票1500股.
3.某中学组织初一学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出了一辆车,且其余客车恰好坐满.已知45座客车日租金为每辆220元, 60座客车日租金为每辆300元,试问:(1)初一年级的人数是多少?原计划租用45座客车多少辆?(2)若租用同一种车,要使每位同学都有座位,怎样租用更合算?
相关课件
这是一份第八章 二元一次方程组【知识梳理课件】——2022-2023学年人教版数学七年级下册单元综合复习,共46页。PPT课件主要包含了复习目标,知识要点,典例讲解,变式训练等内容,欢迎下载使用。
这是一份第八章 二元一次方程组【知识梳理课件】——2022-2023学年人教版数学七年级下册单元综合复习,共46页。PPT课件主要包含了复习目标,知识要点,典例讲解,变式训练等内容,欢迎下载使用。
这是一份第八章 二元一次方程组【知识梳理课件】——2022-2023学年人教版数学七年级下册单元综合复习,共46页。PPT课件主要包含了复习目标,知识要点,典例讲解,变式训练等内容,欢迎下载使用。













