人教版七年级上册第一章 有理数1.2 有理数1.2.1 有理数集体备课ppt课件

这是一份人教版七年级上册第一章 有理数1.2 有理数1.2.1 有理数集体备课ppt课件，共24页。PPT课件主要包含了谁是聪明的人，谁是优秀的人，有理数的基本概念，有理数的运算，相反数，0的相反数是0，0没有倒数，绝对值，有理数大小的比较，运算法则等内容，欢迎下载使用。

聪明的人，从不把同一个错误犯两次！
优秀是一种习惯，希望能从你身上看到这种习惯。 选择从现在开始，让良好的习惯成就自己的未来。
有 理 数 总 复 习
1.负数 2.有理数 3.数轴4.互为相反数5.互为倒数6.有理数的绝对值7.有理数大小的比较8.科学记数法、近似数与有效数字
加、减、乘、除、乘方运算
在正数前面加“—”的数；
0既不是正数，也不是负数.
判断： 1）a一定是正数 2）－a一定是负数 3）－（－a）一定大于0 4）0是正整数
整数和分数统称有理数.
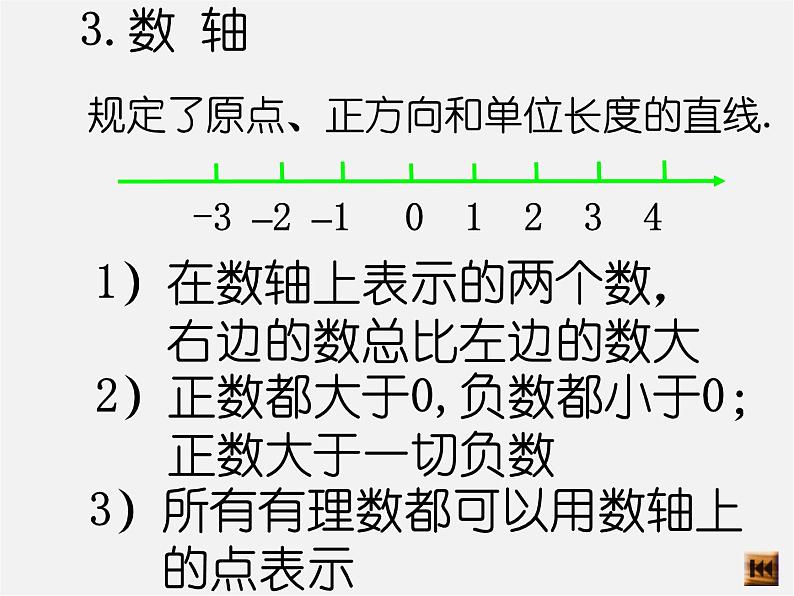
规定了原点、正方向和单位长度的直线.
1）在数轴上表示的两个数， 右边的数总比左边的数大
2）正数都大于0,负数都小于0； 正数大于一切负数
3）所有有理数都可以用数轴上 的点表示
只有符号不同的两个数， 其中一个是另一个的相反数.
1）数a的相反数是-a
3）若a、b互为相反数，则a+b=0
（a是任意一个有理数）
乘积是1的两个数互为倒数.
3）若a与b互为倒数，则ab=1
一个数a的绝对值就是数轴上 表示数a的点与原点的距离.
1）数a的绝对值记作︱a︱
3) 对任何有理数a,总有︱a︱≥0.
1）可通过数轴比较： 在数轴上的两个数，右边的数总比左边的数大； 正数都大于0，负数都小于0；正数大于一切负数.2）两个负数，绝对值大的反而小即:若a＜0,b＜0,且︱a︱＞︱b︱, 则a＜b.
8.科学记数法、近似数与有效数字
1.把一个大于10的数记成a×10n的形式，其中a是整数数位只有一位的数，这种记数法叫做科学记数法.
2.一个近似数，从左边第一个不是0的数字起，到精确到的数位止，所有的数字，都叫做这个数的有效数字.
二、有理数的五种运算
1.运算法则2.运算顺序3.运 算 律
1）有理数加法法则2）有理数减法法则3）有理数乘法法则4）有理数除法法则5）有理数的乘方
① 同号两数相加,取相同的符号,并把绝对值相加。
② 异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值；互为相反数的两数相加得0。
③ 一个数同0相加,仍得这个数。
若a>0,b<0,︱a︱>︱b︱, 则a+b=
用数学语言描述有理数加法法则：
①同号相加： 若a>0,b>0,则a+b=
若a<0,b<0,则a+b=
若a>0,b<0,︱a︱<︱b︱, 则a+b=
若a、b互为相反数，则a+b=
a是任一个有理数，则a+0=
减去一个数， 等于加上这个数的相反数. 即 a-b=a+(-b)
例：分别求出数轴上两点间的距离①表示2的点与表示-7的点②表示-3的点与表示-1的点
解：①︱2-（-7）︱=︱2+7︱=︱9︱=9 ②︱-3-（-1）︱=︱-3+1︱=︱-2︱=2
两数相乘，同号得正，异号得负，并把绝对值相乘； 任何数同0相乘，都得0.
①几个不等于0的数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积为负；当负因数有偶数个时，积为正.
②几个数相乘，有一个因数为0，积就为0.
用数学语言描述有理数乘法法则：
①同号相乘 若a>0,b>0,则 ab =
若a<0,b<0,则 ab =
②异号相乘 若a>0,b<0,则 ab =
若a<0,b>0,则 ab =
a为任何有理数，则 a×0 =
①除以一个数等于乘上这个数的倒数 即
②两数相除,同号得正,异号得负,并把绝对值相除0除以任何一个不等于0的数,都得0
①求n个相同因数的积的运算,叫做乘方.
②正数的任何次幂都是正数； 负数的奇次幂是负数， 负数的偶次幂是正数.
1）有括号，先算括号里面的2）先算乘方，再算乘除， 最后算加减3）对只含乘除，或只含加减的 运算，应从左往右运算
(a+b)+c=a+(b+c)
(ab)c=a(bc)
a(b+c)=ab+ac
1、相反数等于本身的数？
2、绝对值等于本身的数？
3、倒数等于本身的数？
4、平方等于本身的数？
5、立方等于本身的数？
6、非负数有哪些形式？
例题：已知︱a-1︱+( b+2)2 =0,则a=？ b=?