

某校八年级(上)第一次月考数学试卷
展开1. 如图,已知△ABC≅△CDA,则下列结论:
①AB=CD,BC=DA.
②∠BAC=∠DCA,∠ACB=∠CAD.
③AB // CD,BC // DA.
其中正确的是( )
A.①B.②C.①②D.①②③
2. 如图,AB=AC,BD=CD.若∠B=70∘,则∠BAC=( )
A.20∘B.30∘C.40∘D.50∘
3. 如图,已知AB=AC,AD=AE,欲证△ABD≅△ACE,须补充的条件是( )
A.∠B=∠CB.∠D=∠E
C.∠1=∠2D.∠CAD=∠DAC
4. 已知,如图,B,C,E三点在同一条直线上,AC=CD,∠B=∠E=90∘,AB=CE,则不正确的结论是( )
A.∠A与∠D互为余角B.∠A=∠2
C.△ABC≅△CEDD.∠1=∠2
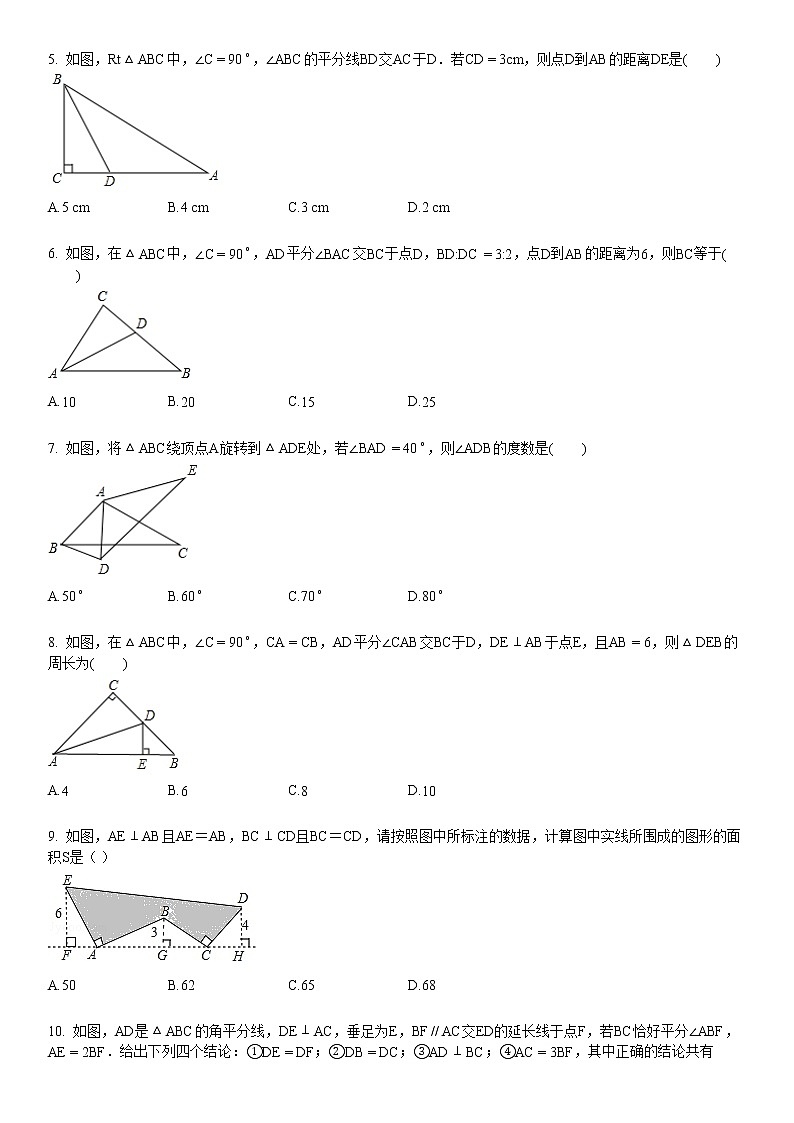
5. 如图,Rt△ABC中,∠C=90∘,∠ABC的平分线BD交AC于D.若CD=3cm,则点D到AB的距离DE是( )
A.5 cmB.4 cmC.3 cmD.2 cm
6. 如图,在△ABC中,∠C=90∘,AD平分∠BAC交BC于点D,BD:DC=3:2,点D到AB的距离为6,则BC等于( )
A.10B.20C.15D.25
7. 如图,将△ABC绕顶点A旋转到△ADE处,若∠BAD=40∘,则∠ADB的度数是( )
A.50∘B.60∘C.70∘D.80∘
8. 如图,在△ABC中,∠C=90∘,CA=CB,AD平分∠CAB交BC于D,DE⊥AB于点E,且AB=6,则△DEB的周长为( )
A.4B.6C.8D.10
9. 如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是( )
A.50B.62C.65D.68
10. 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF // AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
A.4个B.3个C.2个D.1个
二、填空题(本大题共6个小题,每小题3分,共18分)
−23⋅(−2)2=________,(103)2=________,(ab2)3=________.
如图,△ABC中,AD是中线,AC=3,AB=5,则AD的取值范围是________.
如图,OP平分∠MON,PA⊥ON于点A,点Q是射线OM上一个动点,若PA=3,则PQ的最小值为________.
如图,已知△ABC中,∠B=∠ACB,∠BAC和∠ACB的角平分线交于D点.∠ADC=100∘,那么∠CAB是________.
在△ABC中,∠ACB=90∘,AC=BC,点C的坐标为(−1, 0),点A的坐标为(−4, 2),则B点的坐标为________.
如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为60和38,则△EDF的面积为________.
三、解答题(共8题,共72分)
解下列方程组:
13x+5y=19,3x−5y=−1;
23x+y=8,3x+2=y.
解下列不等式组:2x−5<3x,x−22>x3.
计算:
12a2×(−2ab)×(−ab)3;
2(−12xy2)3⋅(2xy3)3⋅y2.
如图,在△ABC中,AC⊥BC,AD是∠BAC平分线,DE⊥AB于E,AB=7cm,AC=3cm,求BE的长.
如图,△ABC中,∠C=90∘,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BE=CF,求证:BD=DF.
黄冈某地“杜鹃节”期间,某公司70名职工组团前往参观欣赏,旅游景点规定:①门票每人60元,无优惠;②上山游玩可坐景点观光车,观光车有四座和十一座车,四座车每辆60元,十一座车每人10元.公司职工正好坐满每辆车且总费用不超过5000元,问公司租用的四座车和十一座车各多少辆?
1如图1,点E,F分别在正方形ABCD的边BC,CD上,∠EAF=45∘,求证:EF=BE+FD.
2如图2,四边形ABCD中,∠BAD≠90∘,AB=AD,∠B+∠D=180∘,点E,F分别在边BC,CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
3如图3,四边形ABCD中,∠BAD≠90∘,AB=AD,AC平分∠BCD,AE⊥BC于E,AF⊥CD交CD延长线于F,请直接写出线段BC,CD与CE之间的数量关系为________(不需证明).
在平面直角坐标系xOy中,已知A(−a, 0),B(0, b),a,b满足(a+b−6)2+|a−2b+3|=0.
1如图1,若C点坐标为(1, 0)且AH⊥BC于H,AH交OB于点P,求P点坐标;
2如图2,若∠APO=45∘,求证:PA⊥PB;
3如图3,若B(0, 3),点D在x轴负半轴上运动,点E在x轴正半轴上运动,满足S△BDE=24,分别以BE,BD为腰作等腰Rt△BEN、等腰Rt△BDM,连结MN交y轴于Q点,OQ的长度是否发生变化?若不变,求出OQ的值;若变化,求OQ的取值范围.
参考答案与试题解析
2016-2017学年湖北省某校八年级(上)第一次月考数学试卷
一、选择题(共10小题,每小题3分,共30分)
1.
【答案】
D
【考点】
全等三角形的性质
【解析】
根据全等三角形的性质得出AB=CD,BC=DA,∠BAC=∠DCA,∠ACB=∠CAD,根据平行线的判定推出即可.
【解答】
解:∵ △ABC≅△CDA,
∴ AB=CD,BC=DA,
∠BAC=∠DCA,∠ACB=∠CAD,
∴ AB // CD,BC // DA,
∴ ①②③都正确.
故选D.
2.
【答案】
C
【考点】
等腰三角形的判定与性质
【解析】
根据等腰三角形的性质即可得到结论
【解答】
解:∵ AB=AC,
∴ ∠C=∠B=70∘,
∴ ∠BAC=180∘−∠B−∠C=40∘,
故选C.
3.
【答案】
C
【考点】
全等三角形的判定
【解析】
已知两边相等,要使两三角形全等必须添加这两边的夹角,即∠BAD=∠CAE,因为∠CAD是公共角,则当∠1=∠2时,即可得到△ABD≅△ACE.
【解答】
解:∵ AB=AC,AD=AE,
∠B=∠C不是已知两边的夹角,A选项不可以;
∠D=∠E不是已知两边的夹角,B选项不可以;
由∠1=∠2得∠BAD=∠CAE,符合SAS,
可以为补充的条件;
∠CAD=∠DAC不是已知两边的夹角,D选项不可以;
故选C.
4.
【答案】
D
【考点】
全等三角形的性质与判定
【解析】
根据HL证Rt△ABC≅Rt△CED,根据全等三角形的性质即可求出答案.
【解答】
解:∵ ∠B=∠E=90∘,
∴ 在Rt△ABC和Rt△CED中
AC=CD,AB=CE,
∴ Rt△ABC≅Rt△CED(HL),故C正确,
∴ ∠A=∠2,∠1=∠D,
∵ ∠1+∠A=90∘,
∴ ∠A+∠D=90∘,∠1+∠2=90∘,
∴ ∠A与∠D互为余角,故A,B正确;D 错误,
故选D.
5.
【答案】
C
【考点】
角平分线的性质
【解析】
过D作DE⊥AB于E,由已知条件,根据角平分线上的点到角的两边的距离相等解答.
【解答】
解:过D作DE⊥AB于E,如图:
∵ BD是∠ABC的平分线,
∠C=90∘,DE⊥AB,
∴ DE=CD,
∵ CD=3cm,
∴ DE=3cm.
故选C.
6.
【答案】
C
【考点】
角平分线的性质
【解析】
先根据角平分线的性质得出CD的长,再由BD:DC=3:2求出BD的长,进而可得出结论.
【解答】
解:∵ 在△ABC中,∠C=90∘,
AD平分∠BAC交BC于点D,
点D到AB的距离为6,
∴ CD=6.
∵ BD:DC=3:2,
∴ BD=32CD=32×6=9,
∴ BC=6+9=15.
故选C.
7.
【答案】
C
【考点】
旋转的性质
【解析】
先根据图形旋转的性质得出AB=AD,再根据等腰三角形的性质即可得出∠ADB的度数.
【解答】
解:∵ △ADE由△ABC旋转而成,
∴ AB=AD,
∵ ∠BAD=40∘,
∴ ∠ADB=180∘−∠BAD2
=180∘−40∘2=70∘.
故选C.
8.
【答案】
B
【考点】
等腰直角三角形
角平分线的性质
全等三角形的性质
【解析】
因为AC和BC相等,所以△ACB是等腰直角三角形,然后又利用角平分线,推出全等,最后得出结果.
【解答】
解:∵ CA=CB,∠C=90∘,
AD平分∠CAB,DE⊥AB于点E,
∴ △ACB为等腰直角三角形,
BC=AC=AE,
∴ Rt△ACD≅Rt△AED(HL),
∴ CD=DE,
∴ △DEB的周长=DE+EB+DB
=CD+DB+EB=CB+EB
=AE+EB=AB=6,
∴ 周长为6.
故选B.
9.
【答案】
A
【考点】
梯形的面积
全等三角形的性质与判定
三角形的面积
直角梯形
【解析】
由AE⊥AB,EF⊥FH,BG⊥AG,可以得到∠EAF=∠ABG,而AE=AB,∠EFA=∠AGB,由此可以证明△EFA≅△ABG,所以AF=BG,AG=EF;
同理证得△BGC≅△DHC,GC=DH,CH=BG.
故FH=FA+AG+GC+CH=3+6+4+3=16,然后利用面积的割补法和面积公式即可求出图形的面积.
【解答】
解:∵ AE⊥AB且AE=AB,
EF⊥FH,BG⊥FH,
⇒∠EAB=∠EFA=∠BGA=90∘,
∠EAF+∠BAG=90∘,
∠ABG+∠BAG=90∘,
⇒∠EAF=∠ABG,
∴ AE=AB,∠EFA=∠AGB,
∠EAF=∠ABG,
⇒△EFA≅△ABG,
∴ AF=BG,AG=EF.
同理证得△BGC≅△CHD.
得GC=DH,CH=BG.
故FH=FA+AG+GC+CH
=3+6+4+3=16,
故S=12(6+4)×16−3×4−6×3
=50.
故选A.
10.
【答案】
A
【考点】
全等三角形的性质
三角形的角平分线
等腰三角形的性质
【解析】
根据等腰三角形的性质三线合一得到BD=CD,AD⊥BC,故②③正确;通过△CDE≅△DBF,得到DE=DF,CE=BF,故①④正确.
【解答】
解:∵ BF // AC,
∴ ∠C=∠CBF,
∵ BC平分∠ABF,
∴ ∠ABC=∠CBF,
∴ ∠C=∠ABC,
∴ AB=AC,
∵ AD是△ABC的角平分线,
∴ BD=CD,AD⊥BC,故②③正确,
在△CDE与△BDF中,
∠C=∠CBF,CD=BD,∠EDC=∠BDF,
∴ △CDE≅△BDF,
∴ DE=DF,CE=BF,故①正确;
∵ AE=2BF,
∴ AC=3BF,故④正确.
故选A.
二、填空题(本大题共6个小题,每小题3分,共18分)
【答案】
−32,106,a3b6
【考点】
幂的乘方与积的乘方
积的乘方及其应用
【解析】
直接利用有理数的乘方运算法则结合幂的乘方运算法则和积的乘方运算法则分别化简求出答案.
【解答】
解:−23⋅(−2)2=−8×4=−32,
(103)2=106,
(ab2)3=a3b6.
故答案为:−32,106,a3b6.
【答案】
1
三角形三边关系
全等三角形的性质
【解析】
延长AD到点E,使AD=ED,连接CE,可证明△ABD≅△ECD,可求得CE=AB,在△ACE中可利用三角形三边关系可求得AE的取值范围,则可求得AD的取值范围.
【解答】
解:延长AD到点E,
使AD=ED,连接CE.
如图:
∵ AD是△ABC的中线,
∴ BD=CD.
在△ABD和△ECD中
AD=ED,∠ADB=∠EDC,BD=CD,
∴ △ABD≅△ECD(SAS),
∴ AB=EC,
在△AEC中,AC+EC>AE,
且EC−AC
∴ 2<2AD<8,
∴ 1
3
【考点】
角平分线的性质
垂线段最短
【解析】
根据垂线段最短可知PQ⊥OM时,PQ的值最小,再根据角平分线上的点到角的两边的距离相等可得PQ=PA.
【解答】
解:根据垂线段最短,PQ⊥OM时,PQ的值最小,
∵ OP平分∠MON,PA⊥ON,
∴ PQ=PA=3.
故答案为:3.
【答案】
140∘
【考点】
三角形内角和定理
角平分线的性质
【解析】
设∠CAB=x,根据已知可以分别表示出∠ACD和∠DAC,再根据三角形内角和定理即可求得∠CAB的度数.
【解答】
解:设∠CAB=x
∵ 在△ABC中,
∠B=∠ACB=12(180∘−x),
∵ CD是∠ACB的角平分线,
AD是∠BAC的角平分线,
∴ ∠ACD=14(180∘−x),∠DAC=12x,
∵ ∠ACD+∠DAC+∠ADC=180∘,
∴ 14(180∘−x)+12x+100∘=180∘,
∴ x=140∘.
故答案是:140∘.
【答案】
(1, 3)
【考点】
等腰直角三角形
全等三角形的性质
坐标与图形性质
【解析】
作辅助线,构建全等三角形,根据AAS证明△AEC≅△CFB,得AE=CF,EC=BF,根据A(−4, 2),C(−1, 0)得出线段的长,从而写出点B的坐标.
【解答】
解:如图,
过A,B作x轴的垂线,垂足分别为E,F,
∴ ∠AEC=∠CFB=90∘,
∴ ∠EAC+∠ACE=90∘,
∵ ∠ACB=90∘,
∴ ∠ACE+∠BCF=90∘,
∴ ∠EAC=∠BCF,
在△AEC和△CFB中,
∵ ∠EAC=∠BCF,∠AEC=∠CFB,AC=BC,
∴ △AEC≅△CFB(AAS),
∴ AE=CF,EC=BF,
∵ A(−4, 2),C(−1, 0),
∴ AE=2,OE=4,OC=1,
∴ BF=EC=4−1=3,
CF=AE=2,
∴ OF=CF−OC=2−1=1,
∴ B点坐标为(1, 3).
故答案为:(1, 3).
【答案】
11
【考点】
全等三角形的性质与判定
角平分线的性质
【解析】
过点D作DH⊥AC于H,根据角平分线上的点到角的两边距离相等可得DF=DH,再利用“HL”证明Rt△ADF和Rt△ADH全等,Rt△DEF和Rt△DGH全等,然后根据全等三角形的面积相等列方程求解.
【解答】
解:过点D作DH⊥AC于H,
如图:
∵ AD是△ABC的角平分线,
DF⊥AB,DH⊥AC,
∴ DF=DH,
在Rt△ADF和Rt△ADH中,
DF=DH,AD=AD,
∴ Rt△ADF≅Rt△ADH(HL),
∴ SRt△ADF=SRt△ADH,
在Rt△DEF和Rt△DGH中,
DE=DG,DF=DH,
∴ Rt△DEF≅Rt△DGH(HL),
∴ SRt△DEF=SRt△DGH,
∵ △ADG和△AED的面积分别为60和38,
∴ 38+SRt△DEF=60−SRt△DGH,
∴ SRt△DEF=11.
故答案为:11.
三、解答题(共8题,共72分)
【答案】
解:13x+5y=19①,3x−5y=−1②,
①+②得:6x=18,
解得:x=3,
把x=3代入①得:y=2,
则方程组的解为x=3,y=2;
23x+y=8①,3x+2=y②,
把②代入①得:6x+2=8,
解得:x=1,
把x=1代入②得:y=5,
则方程组的解为x=1,y=5.
【考点】
加减消元法解二元一次方程组
代入消元法解二元一次方程组
【解析】
(1)方程组利用加减消元法求出解即可;
(2)方程组利用代入消元法求出解即可.
【解答】
解:13x+5y=19①,3x−5y=−1②,
①+②得:6x=18,
解得:x=3,
把x=3代入①得:y=2,
则方程组的解为x=3,y=2;
23x+y=8①,3x+2=y②,
把②代入①得:6x+2=8,
解得:x=1,
把x=1代入②得:y=5,
则方程组的解为x=1,y=5.
【答案】
解:2x−5<3x①,x−22>x3②,
解不等式①得:x>−5,
解不等式②得:x>6,
所以不等式组的解集为:x>6.
【考点】
解一元一次不等式组
【解析】
分别解出两个不等式,进而得出不等式组的解集即可.
【解答】
解:2x−5<3x①,x−22>x3②,
解不等式①得:x>−5,
解不等式②得:x>6,
所以不等式组的解集为:x>6.
【答案】
解:1原式=2a2×2ab×a3b3
=4a6b4;
2原式=−18x3y6⋅8x3y9⋅y2
=−8x6y17.
【考点】
单项式乘单项式
幂的乘方与积的乘方
【解析】
(1)根据单项式乘以单项式的法则进行计算即可;
(2)根据积的乘方和单项式乘以单项式的法则进行计算即可.
【解答】
解:1原式=2a2×2ab×a3b3
=4a6b4;
2原式=−18x3y6⋅8x3y9⋅y2
=−8x6y17.
【答案】
解:∵ AC⊥BC,
AD是∠BAC平分线,
DE⊥AB于E,
∴ DC=DE,
在Rt△ACD和Rt△AED中,
AD=AD,DC=DE,
∴ Rt△ACD≅Rt△AED(HL),
∴ AC=AE=3cm,
∵ AB=7cm,
∴ BE=7−3=4(cm).
【考点】
全等三角形的性质与判定
角平分线的性质
【解析】
直接利用角平分线的性质结合全等三角形的判定与性质得出AE的长,进而得出答案.
【解答】
解:∵ AC⊥BC,
AD是∠BAC平分线,
DE⊥AB于E,
∴ DC=DE,
在Rt△ACD和Rt△AED中,
AD=AD,DC=DE,
∴ Rt△ACD≅Rt△AED(HL),
∴ AC=AE=3cm,
∵ AB=7cm,
∴ BE=7−3=4(cm).
【答案】
证明:如图:
∵ AD是∠BAC的平分线,
DE⊥AB于E,DC⊥AC于C,
∴ DE=DC.
在Rt△CDF和Rt△EDB中,
DC=DE,∠C=∠DEB,CF=BE,
∴ Rt△CDF≅Rt△EDB(SAS),
∴ BD=DF.
【考点】
角平分线的性质
全等三角形的性质
【解析】
根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即DE=CD,再根据HL证明Rt△CDF≅Rt△EBD,从而得出DF=BD.
【解答】
证明:如图:
∵ AD是∠BAC的平分线,
DE⊥AB于E,DC⊥AC于C,
∴ DE=DC.
在Rt△CDF和Rt△EDB中,
DC=DE,∠C=∠DEB,CF=BE,
∴ Rt△CDF≅Rt△EDB(SAS),
∴ BD=DF.
【答案】
解:设四座车租x辆,十一座车租y辆,则有:
4x+11y=70,70×60+60x+11y×10≤5000,
将4x+11y=70变形为:4x=70−11y,
代入70×60+60x+11y×10≤5000,可得:
70×60+15(70−11y)+11y×10≤5000,
解得y≥5011,
又∵ x=70−11y4≥0,
∴ y≤7011,
故y=5,6.
当y=5时,x=154(不合题意舍去).
当y=6时,x=1.
故四座车租1辆,十一座车租6辆.
【考点】
二元一次方程组的应用——其他问题
一元一次不等式的实际应用
【解析】
设四座车租x辆,十一座车租y辆,先根据“共有70名职员”作为相等关系列出x,y的方程,再根据“公司职工正好坐满每辆车且总费用不超过5000元”作为不等关系列不等式,求x,y的整数解即可.注意求得的解要代入实际问题中检验.
【解答】
解:设四座车租x辆,十一座车租y辆,则有:
4x+11y=70,70×60+60x+11y×10≤5000,
将4x+11y=70变形为:4x=70−11y,
代入70×60+60x+11y×10≤5000,可得:
70×60+15(70−11y)+11y×10≤5000,
解得y≥5011,
又∵ x=70−11y4≥0,
∴ y≤7011,
故y=5,6.
当y=5时,x=154(不合题意舍去).
当y=6时,x=1.
故四座车租1辆,十一座车租6辆.
【答案】
1证明:把△ABE绕点A逆时针旋转90∘至△ADG,
如图所示:
则△ADG≅△ABE,
∴ AG=AE,∠DAG=∠BAE,DG=BE,
又∵ ∠EAF=45∘,
即∠DAF+∠BAE=∠EAF=45∘,
∴ ∠GAF=∠FAE,
在△GAF和△FAE中,
AG=AE,∠GAF=∠FAE,AF=AF,
∴ △GAF≅△FAE(SAS).
∴ GF=EF.
又∵ DG=BE,
∴ GF=BE+DF,
∴ BE+DF=EF.
2解:∠BAD=2∠EAF.
理由如下:
如图所示,
延长CB至M,使BM=DF,连接AM,
∵ ∠ABC+∠D=180∘,
∠ABC+∠ABM=180∘,
∴ ∠D=∠ABM,
在△ABM和△ADF中,
AB=AD,∠ABM=∠D,BM=DF,
∴ △ABM≅△ADF(SAS)
∴ AF=AM,∠DAF=∠BAM,
∵ ∠BAD=2∠EAF,
∴ ∠DAF+∠BAE=∠EAF,
∴ ∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
AE=AE,∠FAE=∠MAE,AF=AM,
∴ △FAE≅△MAE(SAS),
∴ EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
BC+CD=2CE
【考点】
全等三角形的性质与判定
四边形综合题
角平分线的性质
【解析】
(1)根据旋转的性质可以得到△ADG≅△ABE,则GF=BE+DF,只要再证明△AFG≅△AFE即可.
(2)延长CB至M,使BM=DF,连接AM,证△ADF≅△ABM,再证△FAE≅△MAE,即可得出答案;
(3)由角平分线的性质得出AE=AF,由HL证明Rt△ABE≅Rt△ADF,得出BE=DF,同理:Rt△ACE≅Rt△ACF,得出CE=CF,即可得出结论.
【解答】
1证明:把△ABE绕点A逆时针旋转90∘至△ADG,
如图所示:
则△ADG≅△ABE,
∴ AG=AE,∠DAG=∠BAE,DG=BE,
又∵ ∠EAF=45∘,
即∠DAF+∠BAE=∠EAF=45∘,
∴ ∠GAF=∠FAE,
在△GAF和△FAE中,
AG=AE,∠GAF=∠FAE,AF=AF,
∴ △GAF≅△FAE(SAS).
∴ GF=EF.
又∵ DG=BE,
∴ GF=BE+DF,
∴ BE+DF=EF.
2解:∠BAD=2∠EAF.
理由如下:
如图2所示,
延长CB至M,使BM=DF,连接AM,
∵ ∠ABC+∠D=180∘,
∠ABC+∠ABM=180∘,
∴ ∠D=∠ABM,
在△ABM和△ADF中,
AB=AD,∠ABM=∠D,BM=DF,
∴ △ABM≅△ADF(SAS)
∴ AF=AM,∠DAF=∠BAM,
∵ ∠BAD=2∠EAF,
∴ ∠DAF+∠BAE=∠EAF,
∴ ∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
AE=AE,∠FAE=∠MAE,AF=AM,
∴ △FAE≅△MAE(SAS),
∴ EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
3解:BC+CD=2CE;
理由如下:
∵ AC平分∠BCD,
AE⊥BC,AF⊥CD,
∴ ∠AEB=∠AFD=90∘,AE=AF,
在Rt△ABE和Rt△ADF中,
AB=AD,AE=AF,
∴ Rt△ABE≅Rt△ADF(HL),
∴ BE=DF,
同理:Rt△ACE≅Rt△ACF,
∴ CE=CF,
∴ BC+CD
=BE+CE+CF−DF=2CE.
故答案为:BC+CD=2CE.
【答案】
解:1由题意得,a+b−6=0,a−2b+3=0,
解得,a=3,b=3,
由题意得,AC=4,OB=3,OC=1,
由勾股定理得,
BC=OB2+OC2=10,
12×AC×OB=12×BC×AH,
即12×4×3=12×10×AH,
解得,AH=6105,
则HC=AC2−AH2=2105,
∵ ∠AHC=∠AOP=90∘,
∠OAP=∠HAC,
∴ △AOP∽△AHC,
∴ AOAH=OPHC,
即36105=OP2105,
解得,OP=1,
∴ 点P的坐标为:(0, 1);
2∵ OA=OB,
∴ ∠OAB=∠OBA=45∘,
∴ ∠APO=∠OBA,
∵ 共圆的四个点所连成同侧共底的两个三角形的顶角相等,
∴ P,A,O,B四点共圆,
∴ ∠APB=∠AOB=90∘,
∴ PA⊥PB;
3OQ的长度不会发生改变.
如图,
过N作NH // BM,交y轴于H,
则∠BNH+∠MBN=180∘,
∵ 等腰Rt△DBM、等腰Rt△EBN,
∴ ∠MBN+∠DBE=180∘,
∴ ∠BNH=∠DBE,
∵ ∠HBN+∠OBE=90∘,
∠DEB+∠OBE=90∘,
∴ ∠HBN=∠DEB,
在△HBN和△DEB中,
∠BNH=∠EDB,BN=BE,∠HBN=∠DEB,
∴ △HBN≅△DEB,
∴ HN=BD,BH=DE,
∴ HN=BM,
∵ NH // BM,
∴ BQ=QH,
∵ S△BDE=24,OB=3,
∴ DE=16,
∴ BH=16,
∴ BQ=QH=8,
∴ OQ=3+8=11.
【考点】
相似三角形的性质与判定
全等三角形的性质与判定
四点共圆
平行四边形的性质
勾股定理
等腰三角形的性质
【解析】
(1)根据非负数的性质求出a、b,得到AC=4,OB=3,OC=1,根据勾股定理求出BC,根据三角形的面积公式求出AH,利用小时三角形的性质求出OP,得到P点坐标;
(2)根据等腰直角三角形的性质、四点共圆证明;
(3)过N作NH // BM,交y轴于H,证明△HBN≅△DEB,根据全等三角形的性质、三角形的面积公式计算即可.
【解答】
解:1由题意得,a+b−6=0,a−2b+3=0,
解得,a=3,b=3,
由题意得,AC=4,OB=3,OC=1,
由勾股定理得,
BC=OB2+OC2=10,
12×AC×OB=12×BC×AH,
即12×4×3=12×10×AH,
解得,AH=6105,
则HC=AC2−AH2=2105,
∵ ∠AHC=∠AOP=90∘,
∠OAP=∠HAC,
∴ △AOP∽△AHC,
∴ AOAH=OPHC,
即36105=OP2105,
解得,OP=1,
∴ 点P的坐标为:(0, 1);
2∵ OA=OB,
∴ ∠OAB=∠OBA=45∘,
∴ ∠APO=∠OBA,
∵ 共圆的四个点所连成同侧共底的两个三角形的顶角相等,
∴ P,A,O,B四点共圆,
∴ ∠APB=∠AOB=90∘,
∴ PA⊥PB;
3OQ的长度不会发生改变.
如图,
过N作NH // BM,交y轴于H,
则∠BNH+∠MBN=180∘,
∵ 等腰Rt△DBM、等腰Rt△EBN,
∴ ∠MBN+∠DBE=180∘,
∴ ∠BNH=∠DBE,
∵ ∠HBN+∠OBE=90∘,
∠DEB+∠OBE=90∘,
∴ ∠HBN=∠DEB,
在△HBN和△DEB中,
∠BNH=∠EDB,BN=BE,∠HBN=∠DEB,
∴ △HBN≅△DEB,
∴ HN=BD,BH=DE,
∴ HN=BM,
∵ NH // BM,
∴ BQ=QH,
∵ S△BDE=24,OB=3,
∴ DE=16,
∴ BH=16,
∴ BQ=QH=8,
∴ OQ=3+8=11.
某校八年级(上)月考数学试卷(12月): 这是一份某校八年级(上)月考数学试卷(12月),共17页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
某校八年级(上)月考数学试卷(12月份): 这是一份某校八年级(上)月考数学试卷(12月份),共15页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
某校八年级(上)月考数学试卷(10月份): 这是一份某校八年级(上)月考数学试卷(10月份),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。












