初中北师大版4 二次函数的应用获奖ppt课件

回顾知识

导入新课

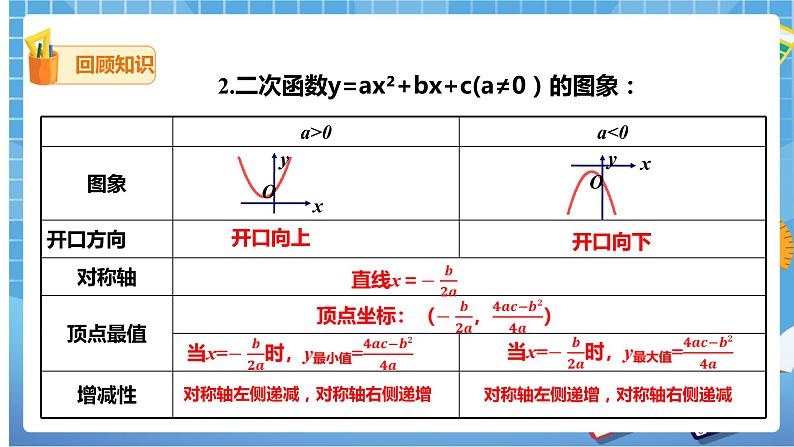
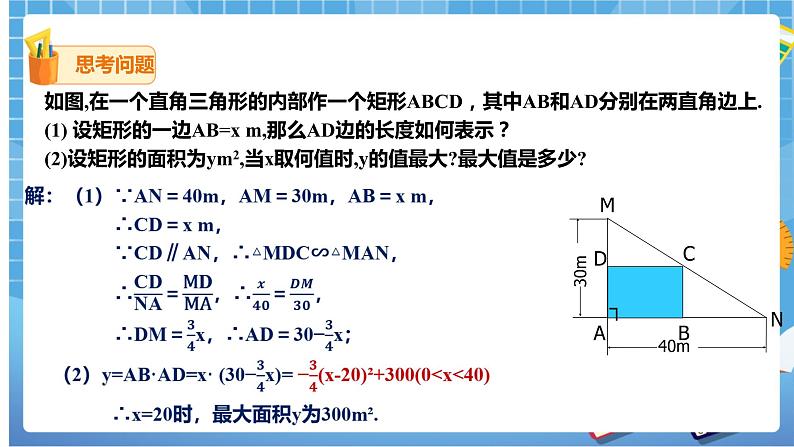
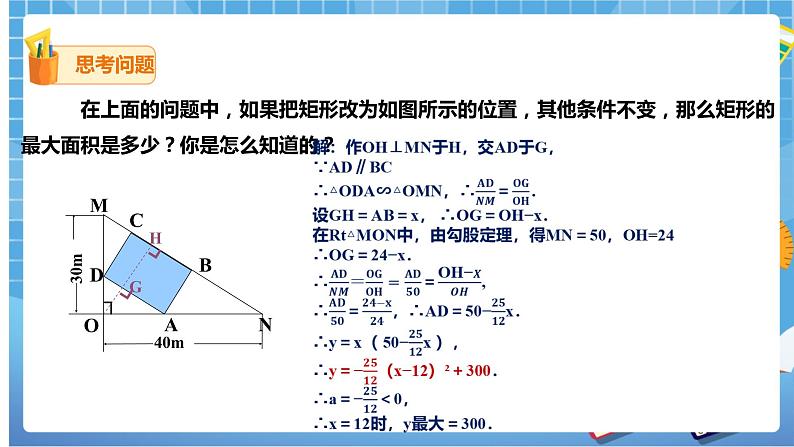
在上节课中，我们已经学习了有关二次函数的相关知识。我们一起回顾下：

1.二次函数表达式是什么呢？

 一般式：y = ax2+bx+c(a≠0)

 顶点式：y =a(x-h)2+k(a≠0)

 交点式：y= a(x-x1)+(x-x2) (a≠0)      

2.二次函数y=ax²+bx+c(a≠0）的图象：

如图,在一个直角三角形的内部作一个矩形ABCD，其中AB和AD分别在两直角边上.

(1) 设矩形的一边AB=x m,那么AD边的长度如何表示？

(2)设矩形的面积为ym2,当x取何值时,y的值最大?最大值是多少?

解：（1）∵AN＝40m，AM＝30m，AB＝x m，

∴CD＝x m，

∵CD∥AN，∴△MDC∽△MAN，

∴＝，∴＝，

∴DM＝x，∴AD＝30−x；

（2）y=AB·AD=x· (30−x)= −(x-20)²+300(0<x<40)

 ∴x=20时，最大面积y为300m².

 在上面的问题中，如果把矩形改为如图所示的位置，其他条件不变，那么矩形的最大面积是多少？你是怎么知道的？

解：作OH⊥MN于H，交AD于G，

∵AD∥BC

∴△ODA∽△OMN，∴＝．

设GH＝AB＝x， ∴OG＝OH−x．

在Rt△MON中，由勾股定理，得MN＝50，OH=24

∴OG＝24−x．

∴＝＝,

∴＝，∴AD＝50−x．

∴y＝x（ 50−x ），

∴y＝−（x−12）²＋300．

∴a＝−＜0，

∴x＝12时，y最大＝300．

学生思考并回答问题。并跟着教师的讲解思路思考问题，并探究知识。

导入新课，利用导入的例子引起学生的注意力。

讲授新课

例题讲解

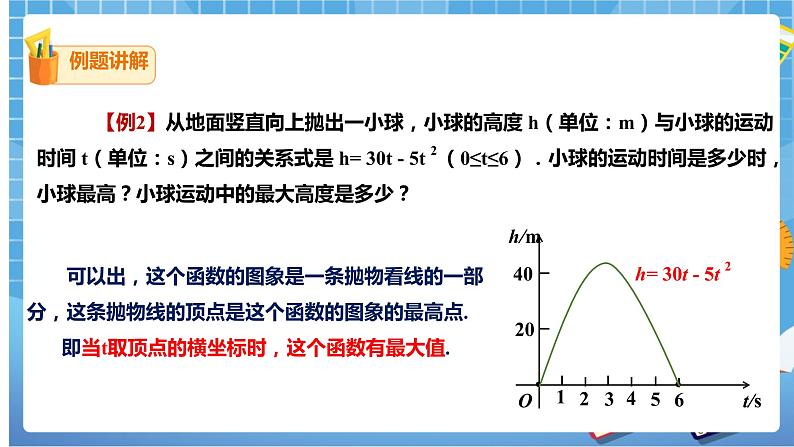
课堂小结

二次函数解决几何面积最值问题的方法

1.建：分析题目，建立二次函数模型，求出函数解析式；

2.求：求出自变量的取值范围；

3.最：配方变形，利用公式求它的最大值或最小值,

4.检：检查求得的最大值或最小值对应的自变量的值必须在自变量的取值范围内.

　　【例1】某建筑物的窗户如图所示,它的上半部是半圆,下半部是矩形,制造窗框的材料总长(图中所有的黑线的长度和)为15m.当x等于多少时,窗户通过的光线最多(结果精确到0.01m)?此时,窗户的面积是多少?

解:∵7x+4y+πx=15，

∴y=

∵0<x<15，且0<<15

∴0<x<1.479

设窗户的面积是Sm²，则

S=x²+2x·

=-x²+x= －x)²+ .

∴当x=≈1.07m时，S最大=≈4.02.

即当x≈1.07m时， S最大≈4.02m².此时，窗户通过的光线最多.

 【例2】从地面竖直向上抛出一小球，小球的高度 h（单位：m）与小球的运动时间 t（单位：s）之间的关系式是 h= 30t - 5t 2 （0≤t≤6）．小球的运动时间是多少时，小球最高？小球运动中的最大高度是多少？

    可以出，这个函数的图象是一条抛物看线的一部分，这条抛物线的顶点是这个函数的图象的最高点.当t取顶点的横坐标时，这个函数有最大值.

如图，在0≤t≤6间，抛物线有最高点.即此时h有最大值.t=- h=45.

小球运动的时间是 3s 时，小球最高.

小球运动中的最大高度是 45 m．

 变式1 如图，用一段长为60m的篱笆围成一个一边靠墙的矩形菜园，墙长32m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？

设垂直于墙的边长为x米，S＝x(60－2x)＝－2x2＋60x.0＜60－2x≤32，即14≤x＜30.

最值在其顶点处，即当x=15m时，S=450m2.

 变式2 如图，用一段长为60m的篱笆围成一个一边靠墙的矩形菜园，墙长18m，这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少？

解：设矩形面积为Sm2,与墙平行的一边为x米，则

S=(0 ＜ x ≤18).

∵30 ＞18，

∴只能利用函数的增减性求其最值.

当x=18时，S有最大值是378.

一起总结下本节课的知识点：

结合导入的思考和老师的讲解，利用探究学习并掌握会利用二次函数的知识解决面积最值问题。

老师在例题讲解的时候，自己先思考，然后再听老师讲解。

跟着老师一起进行本节课的小结，学习一些新的方法。

讲授知识，让学生熟练利用探究学习并掌握会利用二次函数的知识解决面积最值问题。

巩固加深对知识的理解与应用，也让学生知道本节课的学习内容和重点。

固加深对知识的理解与应用，也让学生知道本节课的学习内容和重点。

随堂练习

1.已知一个直角三角形两直角边之和为20cm，则这个直角三角形的最大面积（    B）       

 A.25cm²  A.50cm² A.100cm²  D.不确定

2.用长8cm的铝合金条制成使窗户的透光面积最大的矩形窗框（如图），（那么这个窗户的最大透光面积是（C）       

  A. m² A. cm²  A. m²  D.4m²

3.一个门洞为抛物线形，以门洞底部所在直线为x轴建立平面直角坐标系，抛物线所对应的函数表达式为y=-2x²+3，则2m高处门洞宽为（D ）       

 A.2 m  A. 1cm  A. m  D. m

4.用总长为60m的篱笆围成矩形场地，矩形面积S随矩形一边长l的变化而变化.当l是多少时，场地的面积S最大？

 解:根据题意得:

S=l(30-l),即S=-l2+30l   (0<l<30).

因此，当l=-

S有最大值，S=

也就是说，当l是15m时，场地的面积S最大.

 5.某广告公司设计一幅周长为12m的矩形广告牌，广告设计费用每平方米1000元，设矩形的一边长为x(m),面积为S(m2).

 (1)写出S与x之间的关系式，并写出自变量x的取值范围；

 (2）请你设计一个方案，使获得的设计费最多，并求出这个费用.

 解：（1）设矩形一边长为x，则另一边长为（6-x),

      ∴S=x(6-x)=-x2+6x,其中0＜x<6.

  (2)S=-x2+6x=-(x-3)2+9;

∴当x=3时，即矩形的一边长为3m时，矩形面积最大，为9m2.

这时设计费最多，为9×1000=9000（元）

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

中考链接

1. （2018•沈阳）如图，一块矩形土地ABCD由篱笆围着，并且由一条与CD边平行的篱笆EF分开．已知篱笆的总长为900m（篱笆的厚度忽略不计），当AB＝　      　m时，矩形土地ABCD的面积最大．

 解：设AB＝xm，则BC（900﹣3x），

由题意可得，S＝AB×BC＝x（900﹣3x）（x2﹣300x）（x﹣150）2+33750

∴当x＝150时，S取得最大值，此时，S＝33750，

∴AB＝150m，

故答案为：150．

  2. （2018•绵阳）如图是抛物线型拱桥，当拱顶离水面2m时，水面宽4m，水面下降2m，水面宽度增加　             　m．

 解：如图，建立平面直角坐标系，得抛物线顶点C坐标为（0，2），

设顶点式y＝ax2+2，根据A点坐标（﹣2，0），得出：a＝﹣0.5，

∴抛物线解析式为y＝﹣0.5x2+2，

当水面下降2米，通过抛物线在图上的观察可转化为：

当y＝-2时，对应的抛物线上两点之间的距离，即：

直线y＝-2与抛物线相交的两点之间的距离，此时抛物线解析式得出：﹣2＝﹣0.5x2+2，

解得：x＝±2，

∴水面宽度增加到4米，比原先的宽度当然是增加了（44）米，

故答案为：44．

学生自主完课堂练习中的练习，然后在做完之后根据老师的讲解进一步巩固知识。

借助练习，检测学生的知识掌握程度，同时便于学生巩固知识。

课堂小结

在课堂的最后，我们一起来回忆总结我们这节课所学的知识点：

跟着老师回忆知识，并记忆本节课的知识。

帮助学生加强记忆知识。

板书

图形面积的最大值

借助板书，让学生知识本节课的重点。

课后练习

教材第47页习题2.8第1、2、3题.