北师大版九年级上册4 探索三角形相似的条件图片课件ppt

这是一份北师大版九年级上册4 探索三角形相似的条件图片课件ppt，共22页。PPT课件主要包含了问题2等内容，欢迎下载使用。
问题1：这两个三角形是否为相似形？
相似形定义：我们把形状相同的两个图形称为相似形。
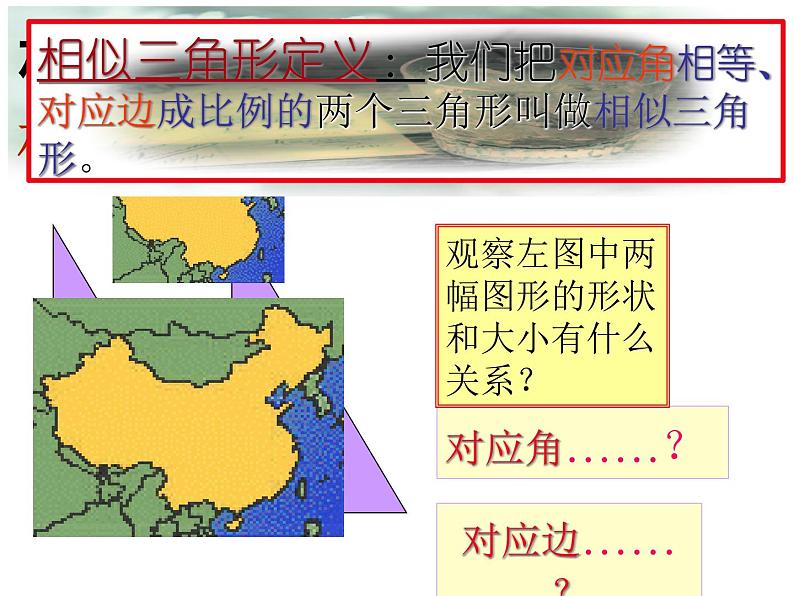
相似三角形定义：我们把对应角相等、对应边成比例的两个三角形叫做相似三角形。
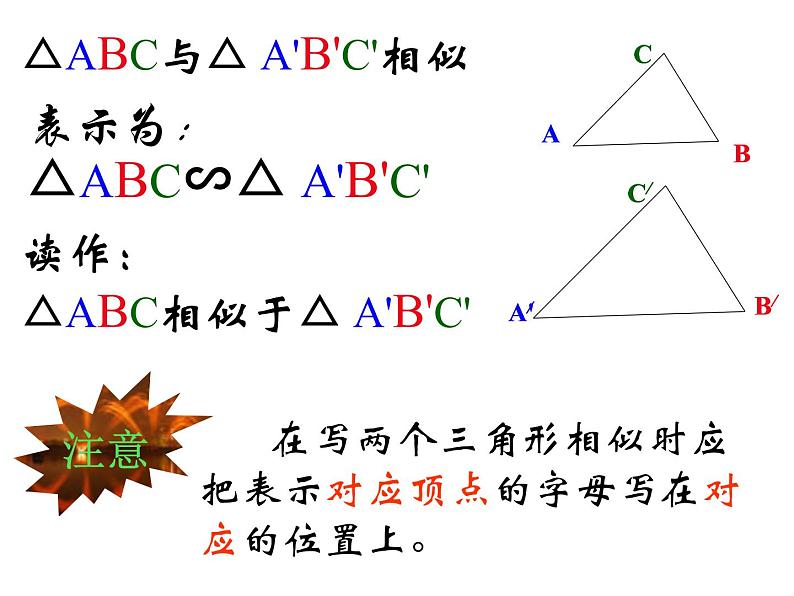
表示为：△ABC∽△ A'B'C'
在写两个三角形相似时应把表示对应顶点的字母写在对应的位置上。
读作：△ABC相似于△ A'B'C'
△ABC与△ A'B'C'相似
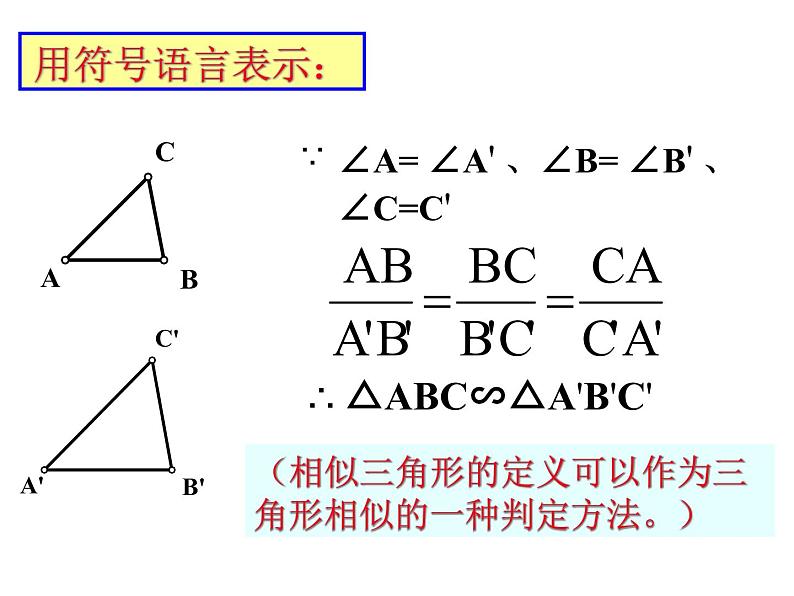
∴ △ABC∽△A'B'C'
（相似三角形的定义可以作为三角形相似的一种判定方法。）
∠ADE=∠B,∠AED=∠C，
∴ △ABC∽△ADE
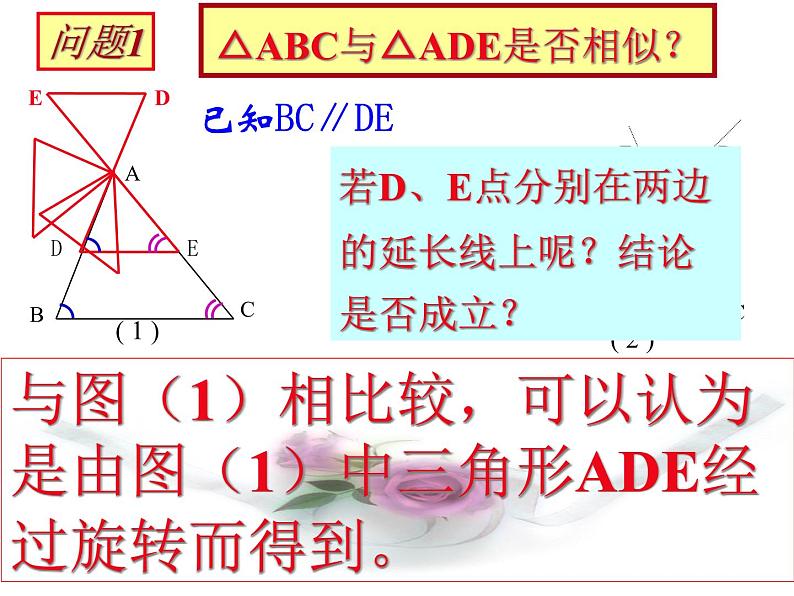
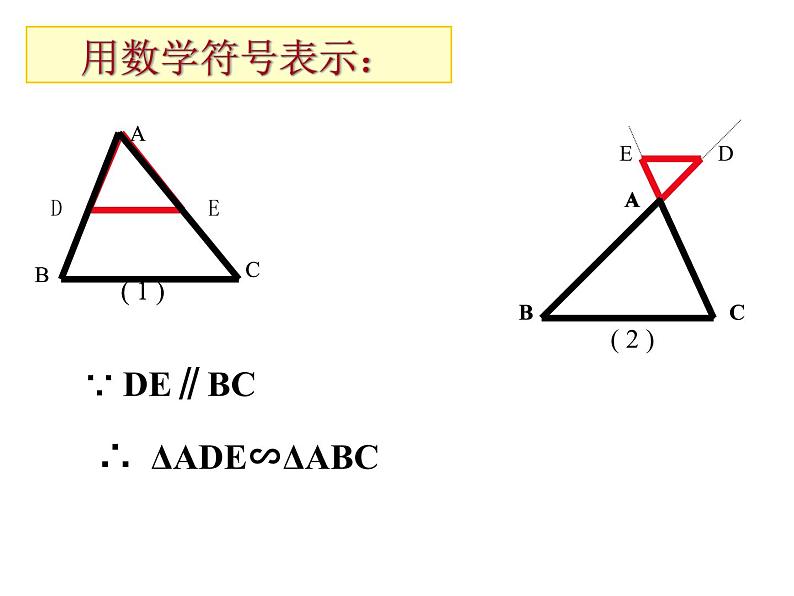
△ABC与△ADE是否相似？
若D、E点分别在两边的延长线上呢？结论是否成立？
与图（1）相比较，可以认为是由图（1）中三角形ADE经过旋转而得到。
相似三角形的预备定理：如果一条直线平行于三角形的一条边，且这条直线与原三角形的两条边 (或其延长线)分别相交，那么所构成的三 角形与原三角形相似。
∴ ΔADE∽ΔABC
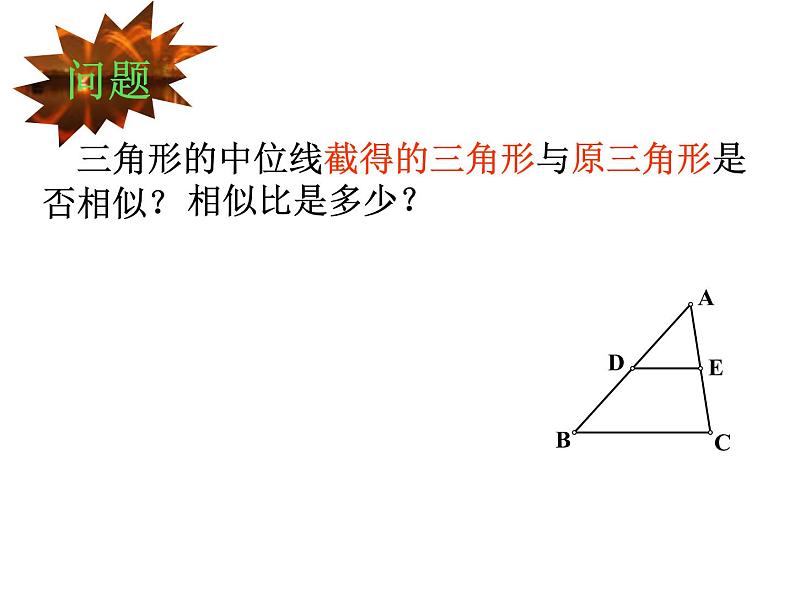
三角形的中位线截得的三角形与原三角形是否相似？
已知：如图，AB∥EF ∥CD，则△AOB与_______和_______都相似。
图中共有____对相似三角形。
△AOB∽ △FOE
在△ABC 和△ 中,
把小的三角形移动到大的三角形上。
利用相似三角形的定义？
利用相似三角形的预备定理？
怎样创造具备预备定理条件的图形？
∠A=∠A'， ∠B'=∠B
判定定理1：如果一个三角形的两个角与另一个三角形的两个角对应相等，那么这两个三角形相似。可以简单说成：两角对应相等，两三角形相似。
∵ AD=A'B',∠A=∠A'，AE=A'C'
∴ ΔA DE≌ΔA'B'C'，
∴ ∠ADE=∠B'，
又∵ ∠B'=∠B，
∴ ∠ADE=∠B，
∴ ΔADE∽ΔABC。
∴ ΔA'B'C'∽ΔABC
解：在AB，AC上分别截取AD= A'B' ，AE = A'C'
∵ ∠A=∠A'， ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
相似三角形的传递性：如果△ABC∽△A1B1C1 ， 而△A1B1C1 ∽△A2B2C2 那么△ABC∽△A2B2C2 。
如果△ABC∽△A1B1C1而△A1B1C1 ∽△A2B2C2那么△ABC与△A2B2C2
（1）ΔABC和ΔDEF中， ∠A=400，∠B=800，∠E=800， ∠F=600。ΔABC与ΔDEF （“相似”或“不相似”）。
(3)在ΔABC中，AB›AC，D为AB边上的一点，过D点作直线DE，交边AC于E点，使ΔADE和ΔABC相似，这样的直线可以作 条
（1）有一个锐角相等的两直角三角形是否为相 似 三角形？
（2）有一个角相等的两等腰三角形是否为相似 三角形？
（1）求证有一个锐角相等的两直角三角形为相似 三角形。
已知DE ∥BC 且∠1=∠B ，则图中共有 对 相似三角形。
∵ ∠1=∠B ，∠A=∠A
∴△ADE∽△ABC∽ △ACD
∵ ∠EDC=∠DCB，
 相似三角形的复习
 相似三角形判定的预备定理
 相似三角形的判定定理1