高考数学专项解题方法归纳探究（全国通用）模板16 空间向量与立体几何专项练习 （原卷版）

这是一份高考数学专项解题方法归纳探究（全国通用）模板16 空间向量与立体几何专项练习 （原卷版），共9页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
模板16空间向量与立体几何专项练习一、单选题1.如图，直三棱柱 中， ，点P在棱 上，且三棱锥A-PBC的体积为4，则直线 与平面PBC所成角的正弦值等于(   )  A. B. C. D.2.如图，三棱锥 的底面ABC是正三角形，侧棱长均相等，P是棱 上的点（不含端点），记直线PB与直线AC所成角为 ，二面角 的平面角为 ，则 不可能是(    )  A.                                         B.                                         C.                                         D. 3.在三棱锥 中， ， ， ， ，平面 平面 ，若球 是三棱锥 的外接球，则球 的半径为（   ）．            A.                                    B.                                    C.                                    D. 4.如图，在正方体ABCD﹣A1B1C1D1中，AM⊥平面A1BD，垂足为M，以下四个结论中正确的个数为（    ）  ①AM垂直于平面CB1D1；②直线AM与BB1所成的角为45°；③AM的延长线过点C1；④直线AM与平面A1B1C1D1所成的角为60°A. 1                                           B. 2                                           C. 3                                           D. 45.已知正方体 的棱长为2，点 在棱 上，过点 作该正方体的截面，当截面平行于平面 且面积为 时，线段 的长为（    ）            A.                                         B. 1                                        C.                                         D. 6.已知六棱锥P﹣ABCDEF的底面是正六边形，PA⊥平面ABC，PA=2AB，则下列命题中错误的是（    ）            A. AE⊥平面PAB  B. 直线PD与平面ABC所成角为45°
C. 平面PBC与平面PEF的交线与直线AD不平行 D. 直线CD与PB所成的角的余弦值为 7.已知 ， 分别是正方体 的棱 ， 上的动点（不与顶点重合），则下列结论正确的是（    ）            A. 平面 与平面 所成的角的大小为定值  B. 
C. 四面体 的体积为定值   D.  平面 8.四棱锥 中，侧面 为等边三角形，底面 为矩形， ， ，点 是棱 的中点，顶点 在底面 的射影为 ，则下列结论正确的是（    ）            A. 棱 上存在点 使得 面
B. 当 落在 上时， 的取值范围是
C. 当 落在 上时，四棱锥 的体积最大值是2
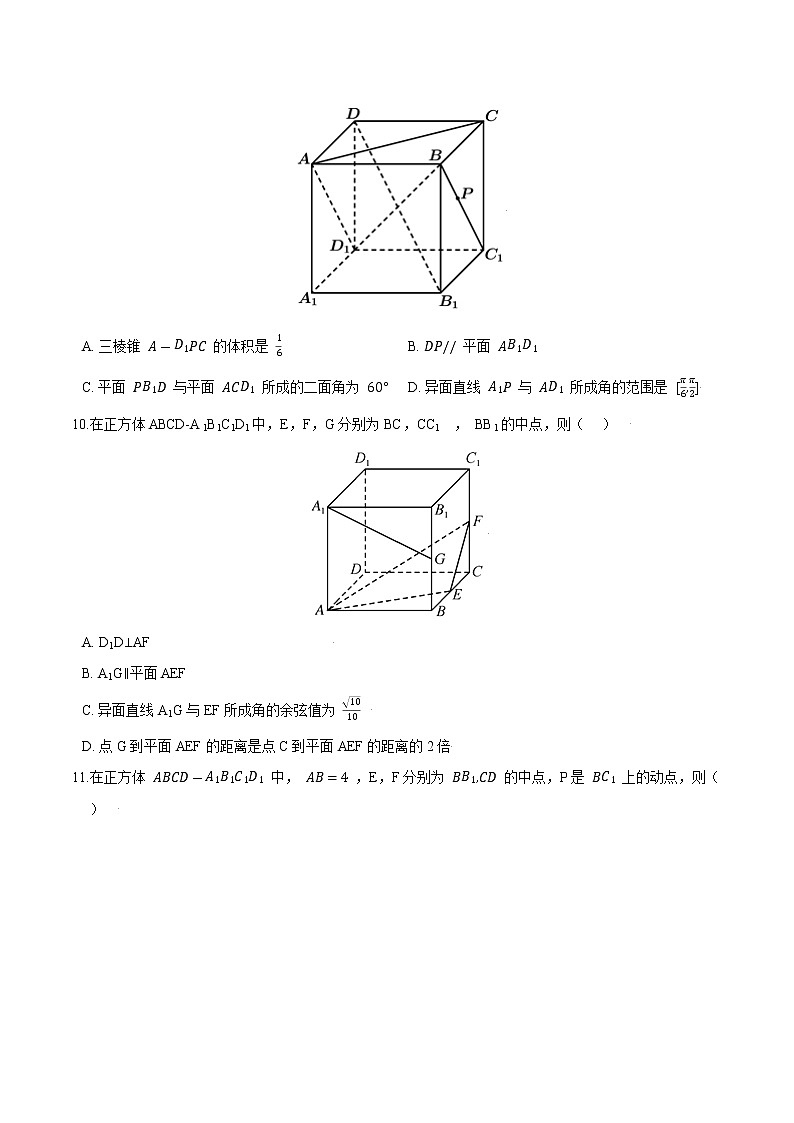
D. 存在 的值使得点 到面 的距离为 二、多选题9.如图，在棱长为1的正方体 中，点 在线段 上运动，则下列判断中正确的是（    ）  A. 三棱锥 的体积是   B.  平面
C. 平面 与平面 所成的二面角为  D. 异面直线 与 所成角的范围是 10.在正方体ABCD-A1B1C1D1中，E，F，G分别为BC，CC1  ， BB1的中点，则（    ）  A. D1D⊥AF                                                    B. A1G∥平面AEF
C. 异面直线A1G与EF所成角的余弦值为    D. 点G到平面AEF的距离是点C到平面AEF的距离的2倍11.在正方体 中， ，E，F分别为 的中点，P是 上的动点，则（    ）  A.  平面
B. 平面 截正方体 的截面面积为18
C. 三棱锥 的体积与P点的位置有关
D. 过 作正方体 的外接球的截面，所得截面圆的面积的最小值为 12.如图，已知长方体 中，四边形 为正方形， ， ， ， 分别为 ， 的中点.则（    ）  A.                                                                  B. 点 ､ ､ ､ 四点共面
C. 直线 与平面 所成角的正切值为      D. 三棱锥 的体积为 三、填空题13.正方体 的棱长为2， ， ， ， 分别是 ， ， ， 的中点，则过 且与 平行的平面截正方体所得截面的面积为________， 和该截面所成角的正弦值为________．    14.如图，已知一个八面体的各条棱长均为 ，四边形 为正方形，给出下列命题：  ①不平行的两条棱所在的直线所成的角是 或 ；  ②四边形 是正方形；③点 到平面 的距离为 ；  ④平面 与平面 所成的锐二面角的余弦值为 ．其中正确的命题全部序号为________15.如图，在正方体 中，点 为线段 的中点，设点 在线段 上二面角 的平面角为 ，用图中字母表示角 为________， 的最小值是________．  16.三棱锥 中， 两两垂直且相等，点 ， 分别是 和 上的动点，且满足 ， ，则 和 所成角余弦值的取值范围是________．    四、解答题17.如图，在四棱锥 中，四边形 为平行四边形， 平面 ， 为 的中点， ， ， .  （1）求证： 平面 ；    （2）求二面角 的正弦值.    18.如图，四棱锥 ，四边形 为平行四边形， ， ， ， ， ， ， 为 中点.  （1）求证： 平面 ；    （2）求证：平面 平面 ；    （3）求二面角 的余弦值.    19.如图，在棱柱 中，底面 为平行四边形， ， ，且 在底面上的投影 恰为 的中点．  （1）过 作与 垂直的平面 ，交棱 于点 ，试确定点 的位置，并说明理由；    （2）若二面角 为 ，求棱柱 的体积．    20.如图，在四棱锥 中，底面 为平行四边形，已知 ， ， 与 .  （1）求证： ；    （2）若平面 平面 ，且 ，求二面角 的余弦值.    21.如图，在四棱锥 中，底面 是平行四边形， ， ， ， ，点 是 的中点．  （1）求证：平面 平面 ；    （2）求二面角 的余弦值．    22.如图，在四棱锥 中，底面 是平行四边形， ，M  ， N分别为 的中点， .  （1）证明： ；    （2）求直线 与平面 所成角的正弦值.