高考数学专项解题方法归纳探究（全国通用）模板16 空间向量与立体几何（解析版）

学校:___________姓名：___________班级：___________考号：___________

模板一、用向量法求空间距离

1.模板解决思路

求点到平面的距离的关键是找到平面的法向量和斜线段对应的向量，然后利用向量的投影求点到面的距离;直线与平面平行时,直线上任一点平面的距离叫直线与平面的距离;异面直线的距离是夹在两条异面直线之间的公垂线段长.

2.模板解决步骤

①第一步；建立空间直角坐标系，将题目中的条件用坐标表示出来,并求出该平面的一个法向量

②第二步；找出从该点出发的平面的任一条斜线段对应的向量

③第三步；求出法向量与斜线段向量的数量积的绝对值再除以法向量的模，即可求出点到平面的距离.

线面距、面面距均可转化为点面距，用求点面距的方法进行求解.

知识点1.求点到直线的距离的一般步骤

(1)求直线的方向向量．

(2)计算所求点与直线上某一点所构成的向量在直线的方向向量上的投影向量的长度．

(3)利用勾股定理求解．另外，要注意平行直线间的距离与点到直线的距离之间的转化．

知识点2.求点面距的步骤

(1)建系：建立恰当的空间直角坐标系．

(2)求点坐标：写出(求出)相关点的坐标．

(3)求向量：求出相关向量的坐标(，α内两不共线向量，平面α的法向量n)．

(4)求距离d＝.

知识点3.空间距离的计算思路

(1)点P到直线l的距离：已知直线l的单位方向向量为u，A是直线l上的定点，P是直线l外一点，设向量在直线l上的投影向量为＝a，则点P到直线l的距离为  (如图)．

(2)设平面α的法向量为n，A是平面α内的定点，P是平面α外一点，则点P到平面α的距离为(如图)．

例题1

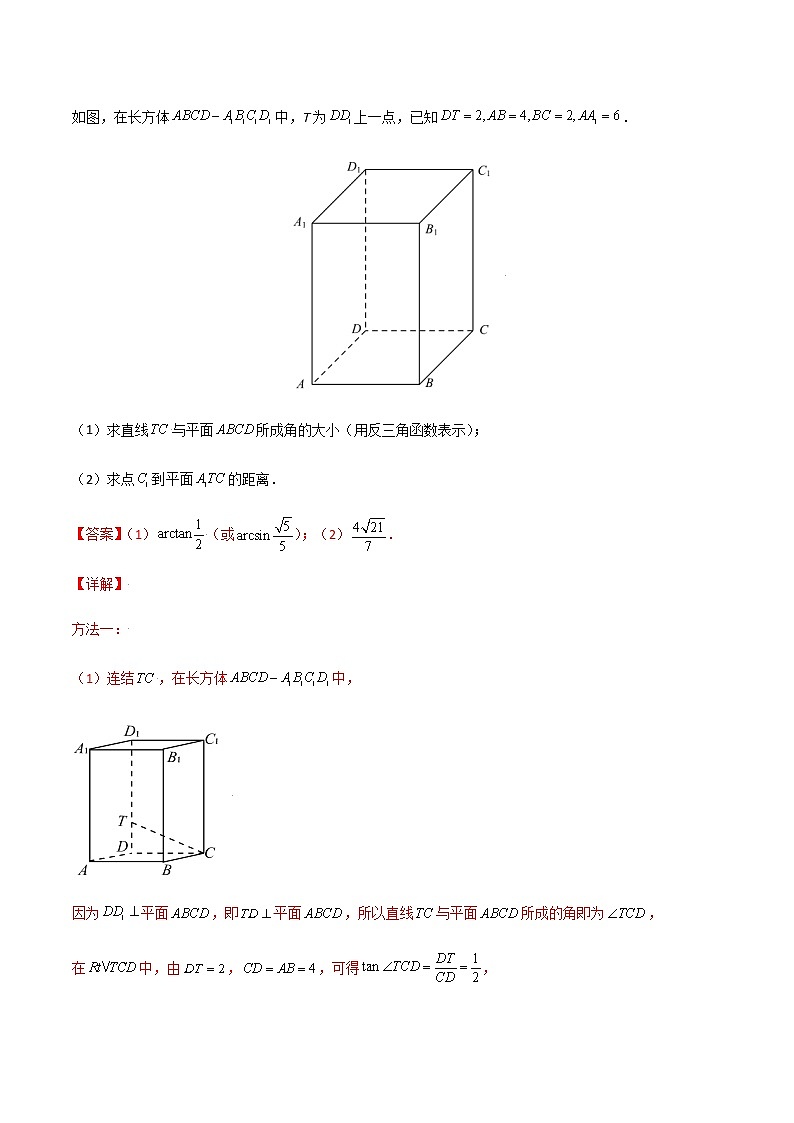
如图，在长方体中，T为上一点，已知．

（1）求直线与平面所成角的大小（用反三角函数表示）；

（2）求点到平面的距离．

【答案】（1）（或）；（2）．

【详解】

方法一：

（1）连结，在长方体中，

因为平面，即平面，所以直线与平面所成的角即为，

在中，由，，可得，

又，故，

所以直线与平面所成角的大小为.

（2）由已知可得，，

所以.又.

设点到平面的距离为.在长方体中，

因为平面，即平面，

再由得，

所以，.

即点到平面的距离为.

方法二：

（1）如图，以为原点，、、分别为、、轴，建立空间直角坐标系.

由已知可得(2，0，0)、(2，4，0)、(0，4，0)、(0，0，0)、(0，0，2)，

故，又平面的一个法向量，

设直线与平面所成角的大小为，

则，注意到，故，

所以直线与平面所成角的大小为.

（2）注意到(0，4，6)，(2，0，6)，及(0，0，2)，(0，4，0)，

故，，，

设平面的一个法向量为，

由已知，得，即，所以，可取，

所以点到平面的距离为.

即点到平面的距离为.

例题2

在长方体中，，过三点的平面截去长方体的一个角后，得到如图所示的几何体.

(1)若的中为，求异面直线与所成角的大小(结果用反三角函数值表示)；

(2)求点到平面的距离.

【答案】

【详解】

(1)按如图所示建立空间直角坐标系

可得点,,,,

由是中点,可得

于是,

设异面直线与所成的角为

则

因此,异面直线与所成的角为: .

(2)设 是平面的法向量

又

  取,可得

即平面的一个法向量是.

.

点到平面的距离.

模板二、用向量法求空间角

1.模板解决思路

求各种角的方法一般都是先确定两个向量(方向向量或者法向量),求这两个向量夹角的余弦值或正弦值，注意确定所求夹角与向量夹角的关系,最后得到所求的角或角的三角函数值.

2.模板解决步骤

①第一步建立空间直角坐标系,将题目中给出的条件用坐标表示出来

第二步将所求角涉及的直线方向向量和平面法向量求出来

第三步代入公式求出角的三角函数值或角

空间向量与空间角的关系

(1)设异面直线l1，l2的方向向量分别为m1，m2，则l1与l2的夹角θ满足cos θ＝|cos〈m1，m2〉|.

(2)设直线l的方向向量和平面α的法向量分别为m，n，则直线l与平面α的夹角θ满足sin θ＝|cos〈m，n〉|.

(3)设n1，n2分别是两个平面α，β的法向量，则两平面α，β夹角θ满足cos θ＝|cos〈m，n〉|.

例题1

将长()､宽()､高()分别为4，3，1的长方体点心盒用彩绳做一个捆扎，有如下两种方案：

方案一：如图（1）传统的十字捆扎；

方案二：如图（2）折线法捆扎，其中．

（1）哪种方案更省彩绳？说明理由：

（2）求平面与平面所成角的余弦值．

【答案】（1）方案②更省彩绳；答案见解析；（2）．

【详解】

（1）方案②更省彩绳．

原因如下：

方案①中彩绳总长度为．

方案②中彩绳总长度为

即，所以方案（2）更省彩绳．【注：只要求出两种方案的长度进行比较即可】

（2）以点为原点，分别为轴建立空间直角坐标系，如图：

则点，

设平面的法向量为，平面的法向量为，

则有，即．令，取

，即，令，取．

所以两个平面所成角的余弦值为．

例题2

某商场共有三层楼，在其圆柱形空间内安装两部等长的扶梯、供顾客乘用．如图，一顾客自一楼点处乘到达二楼的点处后，沿着二楼面上的圆弧逆时针步行至点处，且为弧的中点，再乘到达三楼的点处．设圆柱形空间三个楼面圆的中心分别为、、，半径为米，相邻楼层的间距米，两部电梯与楼面所成角的大小均为．

（1）求此顾客在二楼面上步行的路程；

（2）求异面直线和所成角的大小（结果用反三角函数值表示）．

【答案】（1）米；（2）．

【详解】

（1）过点作一楼面的垂线，垂足为，则落在圆柱底面圆上，

连接，则即为在圆柱下底面上的射影，

所以即为与一楼面所成的角，即．

，所以，，可得．

在中，，则，所以是等腰直角三角形，故．

又因为，所以弧的长为，所以此顾客在二楼面上步行的路程为米；

（2）由（1）可知、、两两互相垂直相交，于是以为坐标原点，以射线、、分别为、、轴建立空间直角坐标系，如图所示．

易得，，、，

向量，，

设异面直线和所成角的大小为，则，

即，所以异面直线和所成角的大小为．